| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Ecuatia lui Schrondinger
Pe baza analogiei unda asociata electronului si vibratia unei corzi fixate la capete ,Shrondinger a incercat sa defineasca starea electronului in atom adoptand prevederi ale probabilitatii.
Sansa de a intalni cel mai des electronul in jurul nucleului este maxima in zona care amplitudinea undei electronice este maxima.
In acustica avem:![]() unde
unde ![]() =
=![]() iar
iar![]() =
=![]()
Prelucrand matematic aceasta ecuatie si folosind ecuatia de Broglie: ![]() v/
v/![]() ;
;![]() se ajunge la ecuatia:
se ajunge la ecuatia: ![]()
Miscarea electronului in atom este in spatiu
si atunci se inlocuieste ![]() cu o functie
cu o functie ![]() sau mult mai bine cu
sau mult mai bine cu ![]() obtinand o ecuatie
celebra:
obtinand o ecuatie
celebra:
![]()
![]() operator Laplace
operator Laplace
De la aceasta ecuatie ,postulata, rezulta concluzii importante care prezinta starea electronului in atom.
Acest lucru rezulta din rezolvarea matematica a a ecuatiei lui
Schrondinger si a conditiilor pe care le impune rezolvarea acesteia, in sensul
ca adopta solutii numai pentru anumite valori ale energiei totale E![]() .Aceste valori se numesc valori proprii, cuantificarea
rezulta asadar fara nici un postulat suplimentar .
.Aceste valori se numesc valori proprii, cuantificarea
rezulta asadar fara nici un postulat suplimentar .
Patratul modulului functiei de unda |![]() |2 este luat drept o masura a
probabilitatii de a gasi electronul intr-un element de volum dV sau mai bine
|2 este luat drept o masura a
probabilitatii de a gasi electronul intr-un element de volum dV sau mai bine ![]() ,reprezentand probabilitatea de a gasi electronul intr-un
strat sferic (sector sferic) de grosime
,reprezentand probabilitatea de a gasi electronul intr-un
strat sferic (sector sferic) de grosime ![]() .
.
De exemplu : pentru n=1 l=0 m=0 avem![]()
![]() ceea ce reprezinta o orbitala sferica
ceea ce reprezinta o orbitala sferica ![]()
In mod analog pentru n=n (n=2,3,4,5,6,7) avem ![]() ceea ce reprezinta orbitale sferice
ceea ce reprezinta orbitale sferice ![]() de grosime
de grosime ![]() in crestere (Forma de
sector de sfera r
in crestere (Forma de
sector de sfera r![]()
![]()
![]()
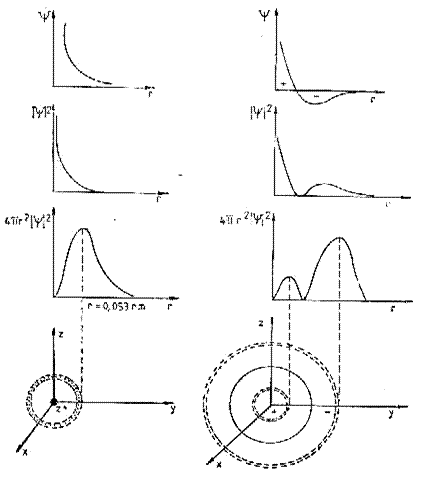
In plan orbitalul de tip s este reprezentata cerc, grosimea liniei cercului fiind grosimea sectorului de sfera.
Pentru n=2 si l=1 m=-1,0,+1 avem trei orbitali ![]() cea ce reprezinta o
orbitala dilobara
cea ce reprezinta o
orbitala dilobara ![]() ; x,y,z fiind axele de
simetrie ale acestora.
; x,y,z fiind axele de
simetrie ale acestora.
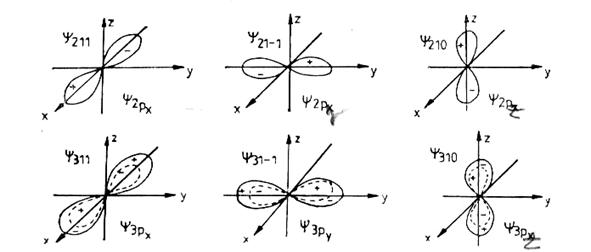
Fig.nr.1.5. Orbitali tip p
Pentru n=3 si l=2 m=-2,-1,0,+1,+2 avem cinci orbitali de geometrie tetralobara: ![]() ceea ce axial
reprezinta
ceea ce axial
reprezinta ![]() si
si ![]() (exceptie, fiind dilobar si cu un inel in jurul sau)
(exceptie, fiind dilobar si cu un inel in jurul sau)
Pentru n=4 si l=3 m=-3,-2,-1,0,+1,+2,+3 avem sapte orbitali de geometrie octolobara.
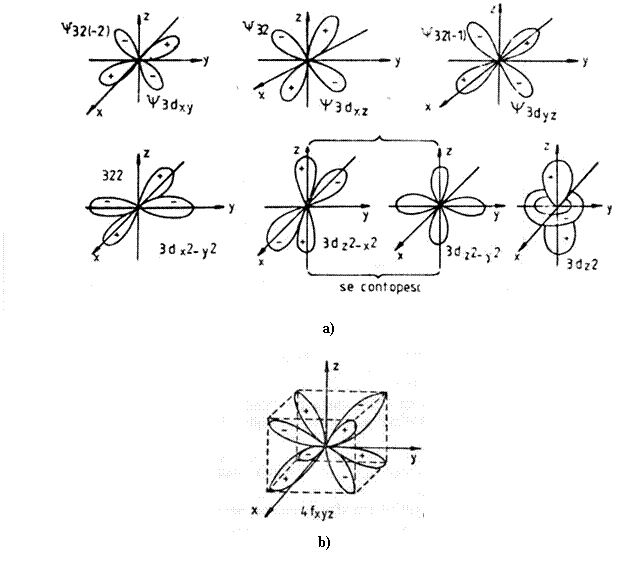
Principii si reguli de constructie a invelisului de electroni
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1770
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved