| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
DINAMICA SISTEMELOR MATERIALE SI A RIGIDULUI
Sistemul material se defineste ca un ansamblu de puncte materiale sau corpuri solide aflate in interactiune mecanica. Daca dimensiunile corpurilor din sistem sunt neglijabile in raport cu distantele dintre ele, acestea pot fi tratate ca sisteme de puncte materiale.
Corpul solid (rigidul) se defineste ca un continuu material nedeformabil putand fi considerat ca limita unui sistem inchis si rigid de puncte materiale care ocupa acelasi domeniu.
In cele ce urmeaza, unele notiuni fundamentale si teoreme generale, stabilite pentru un sistem de puncte materiale sunt extinse la rigid, pe baza unui proces de trecere la limita.
1. NOTIUNI FUNDAMENTALE
1.1. MOMENTE DE INERTIE MASICE
1.1.1. DEFINITII
Momentele de inertie sunt marimi care caracterizeaza modul de distribuire a masei unui sistem material sau rigid in raport cu un reper (plan, axa, pol). Momentele de inertie masice caracterizeaza inertia corpurilor in miscare de rotatie asa cum masa caracterizeaza inertia corpurilor in miscare de translatie.
Considerand un sistem de puncte materiale Ai avand masele mi si distantele in raport cu un reper, li (i = 1, 2,.n), momentul de inertie al sistemului in raport cu reperul considerat are expresia:
|
Fig. 1 |
![]() (1)
(1)
In cazul rigidului, suma se transforma in integrala referitoare la domeniul (D) ocupat de corp.
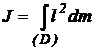 (2)
(2)
Dupa cum lungimea li respectiv l reprezinta distanta la un plan, axa sau pol (punct), momentele de inertie sunt (fig.1):
Momente de inertie planare
Pentru sistem material:
![]() (3)
(3)
Pentru rigid:
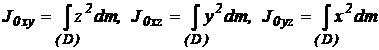 (4)
(4)
Momente de inertie axiale
Pentru sistem material:
![]() (5)
(5)
Pentru rigid:
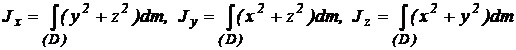 (6)
(6)
Momentul de inertie polar
Pentru sistem material:
![]() (7)
(7)
Pentru rigid:
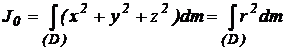 (8)
(8)
Momente de inertie centrifugale
Pentru sistem material:
![]() (9)
(9)
Pentru rigid:
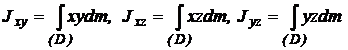 (10)
(10)
1.1.4. VARIATIA MOMENTELOR DE INERTIE IN RAPORT CU AXE PARALELE
Se
da un sistem de puncte materiale Mi
de mase mi cu centrul de
greutate C. Fie o axa Δ care trece prin C si o axa Δ1 paralela cu Δ, distanta dintre cele
doua axe fiind d (fig.2).
Cunoscand momentul de inertie al sistemului JΔ si masa sistemului m sa calculam momentul de inertie ![]() .
.
Se
alege un sistem de referinta Cxyz
cu axa ![]() . Fata de acest triedru, punctul Mi are coordonatele xi, yi, zi.
Se alege un al doilea sistem de referinta O1x1y1z1 care are axele
paralele cu cele ale triedrului precedent, planele de referinta O1x1y1
si Cxy fiind confundate (
. Fata de acest triedru, punctul Mi are coordonatele xi, yi, zi.
Se alege un al doilea sistem de referinta O1x1y1z1 care are axele
paralele cu cele ale triedrului precedent, planele de referinta O1x1y1
si Cxy fiind confundate (![]() ) iar axa
) iar axa ![]() .
.
Fata de acest triedru, punctul Mi are coordonatele x1i, y1i, z1i.
|
Fig. 2 |
Intre coordonatele punctului Mi din planele confundate exista relatiile:
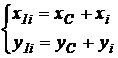
unde: xC si yC sunt coordonatele centrului de greutate C in raport cu sistemul de referinta O1x1y1z1.
Prin definitie:
![]() (5)
(5)
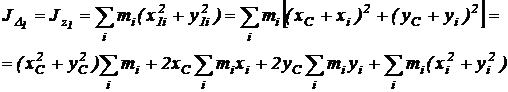 (24)
(24)
Se noteaza:
![]() (25)
(25)
Conform teoremei
momentelor statice si tinand seama ca ![]()
![]() unde ξ si η sunt coordonatele punctului C in sistemul Cxyz,
rezulta:
unde ξ si η sunt coordonatele punctului C in sistemul Cxyz,
rezulta:
![]() (26)
(26)
Introducand relatiile (25) si (26) in (24) se obtine relatia ce defineste teorema Steiner:
![]() (27)
(27)
Momentul de inertie in raport cu o axa Δ1 este egal cu momentul de inertie in raport cu o axa Δ ce trece prin centrul de greutate al sistemului, paralela cu axa Δ1, plus produsul dintre masa sistemului si patratul distantei dintre cele doua axe.
1.1.7. PROPRIETATILE AXELOR PRINCIPALE DE INERTIE
1. Axele principale de inertie formeaza un triedru triortogonal
2. Momentele de inertie centrifugale in raport cu axele principale de inertie sunt nule.
3. Pentru un sistem material sau rigid orice axa de simetrie este axa principala de inertie
4. Pentru un sistem material sau rigid care admite un plan de simetrie, orice axa normala pe acest plan este axa principala de inertie in punctul in care axa intersecteaza planul.
1.2. LUCRUL MECANIC ELEMENTAR AL UNUI SISTEM DE FORTE CARE ACTIONEAZA ASUPRA RIGIDULUI
Se considera un rigid in miscarea
generala, supus actiunii unui sistem de forte ![]() , (fig.10) care actioneaza in punctele Mi (i= 1, 2,,n). In timpul elementar dt, punctul Mi
a carui viteza data de relatia Euler (9.14):
, (fig.10) care actioneaza in punctele Mi (i= 1, 2,,n). In timpul elementar dt, punctul Mi
a carui viteza data de relatia Euler (9.14):
|
Fig. 10 |
![]()
se deplaseaza cu distanta elementara:
![]() (83)
(83)
Lucrul
mecanic elementar al fortei ![]() este:
este:
![]() (84)
(84)
Conform proprietatii produsului mixt, prin permutari se obtine:
![]() (85)
(85)
Introducand
relatia (85) in (84) rezulta lucrul mecanic elementar al fortei ![]() :
:
![]() (86)
(86)
Cu notatiile:
-![]() - deplasarea elementara din miscarea de
translatie a rigidului
- deplasarea elementara din miscarea de
translatie a rigidului
-![]() - rotirea elementara, considerata vector, din
miscarea de rotatie a rigidului
- rotirea elementara, considerata vector, din
miscarea de rotatie a rigidului
-![]() - momentul in raport cu punctul O al fortei
- momentul in raport cu punctul O al fortei ![]()
relatia (86) devine:
![]() (87)
(87)
Pentru
intreg sistemul de forte ![]() , lucrul mecanic elementar devine:
, lucrul mecanic elementar devine:
![]() (88)
(88)
Cum ![]() reprezinta
forta rezultanta si
reprezinta
forta rezultanta si ![]() reprezinta momentul
rezultant, lucrul mecanic elementar al sistemului de forte
reprezinta momentul
rezultant, lucrul mecanic elementar al sistemului de forte ![]() este:
este:
![]() (89)
(89)
In
cazul cand originea sistemului mobil atasat corpului este centrul de
greutate al acestuia ![]() , lucrul mecanic elementar
al sistemului de forte
, lucrul mecanic elementar
al sistemului de forte ![]() este:
este:
![]() (90)
(90)
1.3. IMPULSUL
Fie
un sistem de puncte materiale Mi cu mase mi
si viteze ![]() (i= 1, 2,,n). Impulsul unui punct Mi din sistem este:
(i= 1, 2,,n). Impulsul unui punct Mi din sistem este:
![]() (93)
(93)
iar pentru intreg sistemul material, impulsul devine:
![]() (94)
(94)
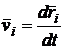 (95)
(95)
introducand relatia (95) in (94) obtinem:
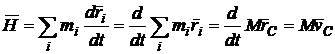 (96)
(96)
unde:
-![]() - conform teoremei momentelor statice
- conform teoremei momentelor statice
-![]() - reprezinta masa sistemului
- reprezinta masa sistemului
-![]() - este vectorul de pozitie al centrului de greutate al
sistemului
- este vectorul de pozitie al centrului de greutate al
sistemului
Cazul rigidului
Impulsul rigidului se obtine prin insumarea la limita a impulsurilor maselor elementare dm pe domeniul ocupat de corp:
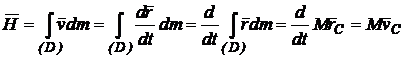 (97)
(97)
unde:
-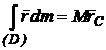 - conform teoremei momentelor statice
- conform teoremei momentelor statice
-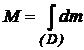 - reprezinta masa rigidului
- reprezinta masa rigidului
-![]() - este vectorul de pozitie al centrului de greutate al
rigidului
- este vectorul de pozitie al centrului de greutate al
rigidului
Impulsul unui sistem material sau rigid nu depinde de felul miscarii; se calculeaza considerand masa concentrata in centrul de greutate, in deplasarea cu viteza acestuia.
1.4. MOMENTUL CINETIC
Cazul sistemului material
Se
considera un sistem de puncte materiale Mi cu mase
mi, viteze ![]() si
vectori de pozitie in raport cu punctul fix O,
si
vectori de pozitie in raport cu punctul fix O, ![]() (i= 1, 2,,n).
(i= 1, 2,,n).
Momentul cinetic al unui punct Mi este:
![]() (98)
(98)
iar pentru intregul sistem devine:
![]() (99)
(99)
Cazul rigidului
Momentul cinetic al rigidului in raport cu un punct fix O1 se obtine prin insumarea la limita a momentelor cinetice ale maselor elementare dm pe domeniul ocupat de corp:
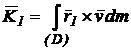 (100)
(100)
Cum ![]() , introducand aceasta expresie in (100) obtinem:
, introducand aceasta expresie in (100) obtinem:
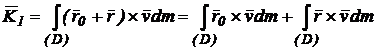 (101)
(101)
unde:
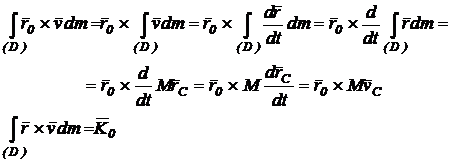 (102)
(102)
in care ![]() reprezinta
momentul cinetic al rigidului calculat in raport cu originea sistemului mobil
atasat rigidului, O.
reprezinta
momentul cinetic al rigidului calculat in raport cu originea sistemului mobil
atasat rigidului, O.
Din relatiile (101) si (102) obtinem:
![]() (103)
(103)
In
cazul in care originea sistemului mobil atasat rigidului este centrul de
greutate al acestuia ![]() , expresia momentului cinetic calculat in raport cu un punct
fix O1 devine:
, expresia momentului cinetic calculat in raport cu un punct
fix O1 devine:
![]() (104)
(104)
care exprima teorema Koenig pentru momentul cinetic al rigidului in miscare fata de un reper fix.
Momentul cinetic al unui rigid, in raport cu un punct fix este egal cu suma dintre momentul cinetic al unui punct material fictiv avand masa corpului situat in centrul de greutate care se deplaseaza cu viteza acestuia si momentul cinetic al rigidului din miscarea relativa fata de centrul sau de greutate.
Specific
miscarii de translatie este viteza aceeasi pentru toate
punctele rigidului, egala cu viteza centrului de greutate ![]() ; Considerand originea sistemului mobil atasat rigidului
ca fiind centrul de greutate
; Considerand originea sistemului mobil atasat rigidului
ca fiind centrul de greutate ![]() , aceasta implica
, aceasta implica ![]() si
si ![]() iar expresia (104)
devine:
iar expresia (104)
devine:
![]() (105)
(105)
In miscarea de translatie, momentul cinetic se calculeaza ca si cum toata masa corpului ar fi concentrata in centrul de greutate si se deplaseaza cu viteza acestuia
Considerand
originile celor doua sisteme de referinta identice ![]() , deci
, deci ![]() si viteza unei
mase elementare a rigidului
si viteza unei
mase elementare a rigidului ![]() , unde
, unde ![]() si
si ![]() sunt exprimati
prin proiectii pe axele sistemului mobil Oxyz
sunt exprimati
prin proiectii pe axele sistemului mobil Oxyz
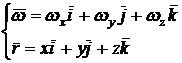 (106)
(106)
expresia momentului cinetic al rigidului devine:
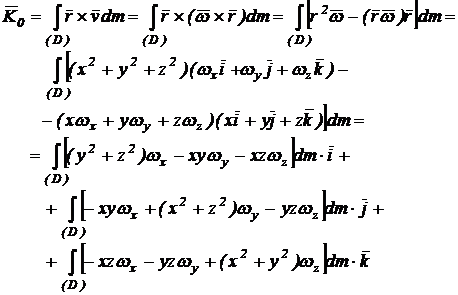
Conform relatiilor de definitie, termenii din integrale reprezinta momentele de inertie axiale (6) si centrifugale (10) ale rigidului, astfel incat momentul cinetic se scrie sub forma:
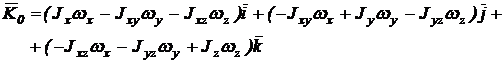 (107)
(107)
Din relatia (107) rezulta expresiile componentelor pe axe ale momentului cinetic:
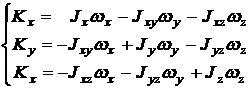 (108)
(108)
1. Axa Oz coincide cu axa de rotatie:
![]() (109)
(109)
Introducand conditia (109) in (10.107) obtinem:
![]() (110)
(110)
2. Axa Oz coincide cu axa de rotatie si este axa de simetrie a rigidului de revolutie:
![]() (111)
(111)
Introducand conditia (111) in (107) obtinem:
![]() (112)
(112)
1.5. ENERGIA CINETICA
Cazul sistemului material
Pentru
un punct material Mi cu masa mi,
viteza ![]() , energia cinetica este:
, energia cinetica este:
![]() (113)
(113)
Pentru
un sistem de puncte materiale Mi cu mase mi,
viteze ![]() (i= 1, 2,,n), energia cinetica
este:
(i= 1, 2,,n), energia cinetica
este:
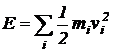 (114)
(114)
Cazul rigidului
In
cazul rigidului prin discretizare la limita in mase elementare dm a caror viteze sunt ![]() , expresia energiei cinetice este:
, expresia energiei cinetice este:
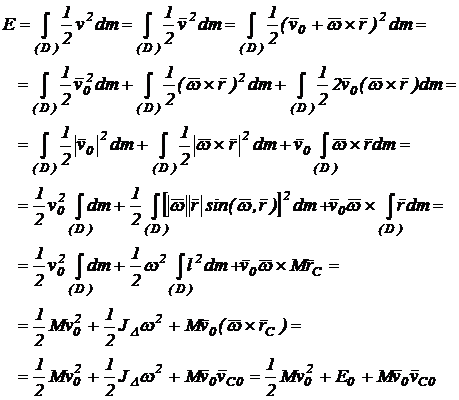 (115)
(115)
In obtinerea expresiei (115) s-au avut in vedere urmatoarele:
-![]() - reprezinta distanta elementului de masa dm la axa de rotatie Δ care trece prin O
- reprezinta distanta elementului de masa dm la axa de rotatie Δ care trece prin O
-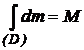 - este masa corpului
- este masa corpului
-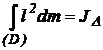 - reprezinta momentul de inertie al corpului in
raport cu axa Δ
- reprezinta momentul de inertie al corpului in
raport cu axa Δ
-![]() - viteza unghiulara care este un vector liber, deci o
marime constanta pentru domeniul de integrare (D) ocupat de corp
- viteza unghiulara care este un vector liber, deci o
marime constanta pentru domeniul de integrare (D) ocupat de corp
-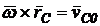 - reprezinta viteza centrului de greutate C din miscarea in raport cu
originea O a sistemului mobil
atasat corpului
- reprezinta viteza centrului de greutate C din miscarea in raport cu
originea O a sistemului mobil
atasat corpului
In cazul
in care originea sistemului mobil atasat rigidului este centrul de
greutate al acestuia ![]() (un punct intrinsec al
rigidului care nu depinde de sistemul de axe fata de care este
calculat), expresia energiei cinetice devine:
(un punct intrinsec al
rigidului care nu depinde de sistemul de axe fata de care este
calculat), expresia energiei cinetice devine:
![]() (116)
(116)
care exprima teorema Koenig pentru energiea cinetica a rigidului in miscare fata de un reper fix.
Energia cinetica a unui rigid,in miscarea fata de un sistem fix este egala cu suma dintre energia cinetica a unui punct material fictiv avand masa corpului situat in centrul de greutate care se deplaseaza cu viteza acestuia si energia cinetica a rigidului din miscarea relativa fata de centrul sau de greutate.
Considerand
originea sistemului mobil ca fiind centrul de greutate ![]() , si viteza in miscarea de translatie fiind
aceeasi pentru toate punctele rigidului,
, si viteza in miscarea de translatie fiind
aceeasi pentru toate punctele rigidului, ![]() expresia energiei
cinetice (116) devine:
expresia energiei
cinetice (116) devine:
![]() (117)
(117)
2. Rigid in miscare de rotatie (cu axa fixa)
Pentru
rigidul in miscare de rotatie in jurul unei axe Δ care trece prin ![]() ,
, ![]() . Introducand aceasta conditie in (115)
rezulta:
. Introducand aceasta conditie in (115)
rezulta:
![]() (118)
(118)
3. Rigid in miscare elicoidala
Viteza
originii sistemului mobil atasat rigidului fiind ![]() si orientata
pe axa miscarii elicoidale Δ
in jurul careia se roteste cu viteza unghiulara
si orientata
pe axa miscarii elicoidale Δ
in jurul careia se roteste cu viteza unghiulara ![]() , energia cinetica definita de (115) are expresia:
, energia cinetica definita de (115) are expresia:
![]() (119)
(119)
Termenul ![]() , intrucat reprezinta un produs mixt cu doi vectori
coliniari,
, intrucat reprezinta un produs mixt cu doi vectori
coliniari, ![]() .
.
4. Rigid in miscare plan paralela
Considerand
originea sistemului mobil in centrul de greutate al corpului ![]() si planul
miscarii pependicular pe axa instantanee de rotatie adica
si planul
miscarii pependicular pe axa instantanee de rotatie adica ![]() , expresia energiei cinetice este data de relatia (116):
, expresia energiei cinetice este data de relatia (116):
![]() (120)
(120)
unde ![]() reprezinta
momentul de inertie al corpului in raport cu axa de rotatie care
trece prin C, perpendiculara pe
planul miscarii.
reprezinta
momentul de inertie al corpului in raport cu axa de rotatie care
trece prin C, perpendiculara pe
planul miscarii.
In multe aplicatii, miscarea plan paralela este tratata ca o rotatie in jurul centrului instantaneu I si prin urmare, energia cinetica a rigidului se va determina corespunzator miscarii de rotatie, momentul de inertie al corpului fiind JI.
Conform teoremei Steiner, relatia intre momentele de inertie JI si JC este:
![]() (121)
(121)
Din distributia de viteze fata de centrul instantaneu de rotatie, viteza centrului de greutate C este:
![]() (122)
(122)
unde: ![]() , (IC) reprezentand
distanta de la centrul instantaneu de rotatie I, la centrul de greutate al corpului C.
, (IC) reprezentand
distanta de la centrul instantaneu de rotatie I, la centrul de greutate al corpului C.
Inlocuind relatiile (122) si (121) in (120) obtinem relatia:
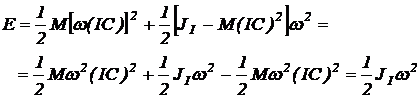 (123)
(123)
2. TEOREMELE GENERALE IN DINAMICA SISTEMELOR MATERIALE SI A RIGIDULUI
2.1. TEOREMA IMPULSULUI
Pentru un sistem material sau rigid, impulsul este definit de relatia (94)
![]()
Derivand in raport cu timpul rezulta:
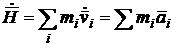 (129)
(129)
Pentru punctul material Mi de masa mi din sistem, legea fundamentala devine:
![]() (130)
(130)
Insumand pe intregul sistem material obtinem:
![]() (131)
(131)
unde: ![]() reprezinta
rezultanta fortelor exterioare sistemului (direct aplicate si de
legatura) iar
reprezinta
rezultanta fortelor exterioare sistemului (direct aplicate si de
legatura) iar ![]() reprezinta
rezultanta fortelor interioare sistemului.
reprezinta
rezultanta fortelor interioare sistemului.
Conform principiului actiunii si reactiunii:
![]() (132)
(132)
Introducand relatiile (131) si (132) in (129) se obtine expresia ce exprima teorema impulsului in cazul sistemului material sau rigid:
![]() (133)
(133)
Derivata in raport cu timpul a impulsului unui sistem material sau rigid este egala cu rezultanta fortelor exterioare care actioneaza asupra sistemului sau rigidului.
Proiectand pe axe relatia vectoriala (10.133) se obtine:
![]() (134)
(134)
Derivata in raport cu timpul a proiectiei pe o axa a impulsului unui sistem material sau rigid este egala cu proiectia pe acea axa a rezultantei fortelor exterioare care actioneaza asupra sistemului sau rigidului.
Daca in timpul miscarii sistemul material sau rigidul este izolat, atunci:
![]() (137)
(137)
Daca sistemul sau rigidul este izolat, atunci impulsul se conserva adica are o valoare constanta care se determina din conditiile initiale ale miscarii.
In multe cazuri, rezultanta fortelor exterioare are nula, componenta dupa o axa, ceea ce conduce la conservarea impulsului dupa acea axa.
Astfel, daca
![]() (138)
(138)
Daca proiectia pe o axa a rezultantei fortelor exterioare este nula, atunci proiectia impulsului pe axa respectiva se conserva adica are o valoare constanta care se determina din conditiile initiale ale miscarii.
2.2. TEOREMA MOMENTULUI CINETIC
Pentru un sistem material sau rigid, momentul cinetic calculat in raport cu un punct fix O, conform relatiei (99) este:
![]()
Derivand in raport cu timpul aceasta relatie se obtine:
![]() (139)
(139)
intrucat: ![]() reprezinta un
produs vectorial cu vectori coliniari
reprezinta un
produs vectorial cu vectori coliniari
Conform relatiei (131):
![]()
care introdusa in (139) se obtine:
![]() (140)
(140)
Se noteaza:
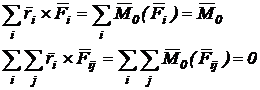 (141)
(141)
unde ![]() reprezinta
momentul in raport cu punctul O al
fortelor exterioare sistemului si
reprezinta
momentul in raport cu punctul O al
fortelor exterioare sistemului si ![]() reprezinta
momentul in raport cu punctul O al
fortelor interioare sistemului si care este nul deoarece momentul in
raport cu acest punct al fiecarei perechi de forte interioare este
nul.
reprezinta
momentul in raport cu punctul O al
fortelor interioare sistemului si care este nul deoarece momentul in
raport cu acest punct al fiecarei perechi de forte interioare este
nul.
Introducand (141) in (140) rezulta expresia vectoriala a teoremei momentului cinetic:
![]() (142)
(142)
Derivata in raport cu timpul a momentului cinetic al unui sistem material sau rigid, calculat in raport cu un punct fix O este egala cu momentul rezultant al fortelor exterioare sistemului sau rigidului, calculat in raport cu acelasi punct.
In
cazul in care originea sistemului mobil atasat rigidului este centrul de
greutate al acestuia ![]() , expresia momentului cinetic calculat in raport cu un punct
fix O1,conform
relatiei (104) este:
, expresia momentului cinetic calculat in raport cu un punct
fix O1,conform
relatiei (104) este:
![]()
care exprima teorema Koenig pentru momentul cinetic al rigidului in miscare fata de un reper fix.
Momentul in raport cu punctul fix O1 al fortelor care actioneaza asupra rigidului este:
![]() (143)
(143)
unde: ![]()
Teorema momentului cinetic devine:
![]() (144)
(144)
respectiv:
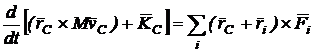
adica:
![]() (145)
(145)
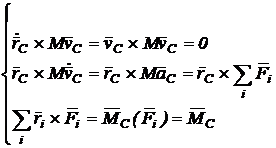 (146)
(146)
Introducand relatiile (146) in (145) rezulta:
![]() (147)
(147)
care exprima teorema momentului cinetic din miscarea rigidului in raport cu centrul de greutate.
Derivata in raport cu timpul a momentului cinetic al unui sistem material sau rigid in miscarea relativa fata de centrul de greutate C, calculat in raport cu acest punct este egala cu momentul rezultant al fortelor exterioare rigidului, calculat in raport cu acelasi punct.
Teorema momentului cinetic pastreaza aceeasi forma in miscarea relativa fata de centrul de greutate ca si in miscarea fata de un punct fix
Proiectand pe axe relatia vectoriala (10.142) se obtine:
![]() (148)
(148)
Derivata in raport cu timpul a proiectiei pe o axa a momentului cinetic al unui sistem material sau rigid calculat in raport cu un punct fix O este egala cu proiectia pe acea axa a momentului rezultant al fortelor exterioare care actioneaza asupra sistemului sau rigidului, calculat in raport cu acelasi punct
Daca in timpul miscarii sistemul material sau rigidul este izolat, atunci:
![]() (149)
(149)
Daca sistemul sau rigidul este izolat, atunci momentul cinetic se conserva adica are o valoare constanta care se determina din conditiile initiale ale miscarii.
Sunt situatii cand momentul rezultant al fortelor exterioare are nula doar componenta dupa o axa, ceea ce conduce la conservarea momentului cinetic dupa acea axa. Astfel, daca:
![]() (150)
(150)
Daca proiectia pe o axa a momentului rezultant al fortelor exterioare este nula, atunci proiectia momentului cinetic pe axa respectiva se conserva adica are o valoare constanta care se determina din conditiile initiale ale miscarii.
2.3. TEOREMA ENERGIEI CINETICE
Cazul miscarii absolute a sistemului material sau a rigidului in raport cu un reper fix.
Pentru un sistem material, energia cinetica este data de relatia (114):
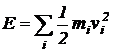
Diferentiind expresia (10.115) obtinem:
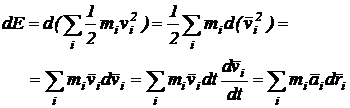 (152)
(152)
Se
considera sistemul material actionat in punctele Mi de fortele exterioare ![]() si fortele
interioare
si fortele
interioare ![]() . Pentru punctul material Mi
de masa mi, legea
fundamentala este data de relatia (130):
. Pentru punctul material Mi
de masa mi, legea
fundamentala este data de relatia (130):
![]()
Inmultind
relatia (130) cu variatia vectorului de pozitie al masei mi, ![]() si insumand
pentru toate punctele din sistem obtinem:
si insumand
pentru toate punctele din sistem obtinem:
![]() (153)
(153)
![]() (154)
(154)
unde ![]() si
si ![]() reprezinta lucrul
mecanic elementar al fortelor exterioare, respectiv interioare sistemului.
reprezinta lucrul
mecanic elementar al fortelor exterioare, respectiv interioare sistemului.
Introducand relatiile (153) si (154) in (152) rezulta teorema energiei cinetice pentru un sistem material:
![]() (155)
(155)
Variatia energiei cinetice in timpul elementar dt este egala cu lucrul mecanic elementar al fortelor exterioare si interioare sistemului efectuat in acelasi interval de timp.
Vor fi analizate cazurile posibile cand lucrul mecanic elementar al fortelor interioare este nul:
![]() (156)
(156)
Pentru
simplificare se considera cazul unei perechi de forte interioare ![]() si
si ![]() care
actioneaza punctele materiale Mi
si Mj ale sistemului
(fig.11).
care
actioneaza punctele materiale Mi
si Mj ale sistemului
(fig.11).
![]() (157)
(157)
deoarece: ![]() iar
iar ![]() reprezinta viteza
relativa din miscarea punctului Mi
fata de Mj ca
si cand acesta ar fi fix; deci
reprezinta viteza
relativa din miscarea punctului Mi
fata de Mj ca
si cand acesta ar fi fix; deci ![]() .
.
|
Fig. 11 |
Cazurile cand ![]() :
:
![]() - in legatura
dintre doua puncte materiale nu se manifesta fortele de
legatura interioare;
- in legatura
dintre doua puncte materiale nu se manifesta fortele de
legatura interioare;
![]() - viteza relativa
dintre puncte este nula;
- viteza relativa
dintre puncte este nula;
![]() - vectorii
- vectorii ![]() si
si ![]() sunt perpendiculari,
ca in cazul a doua corpuri legate printr-un fir inextensibil, perfect
intins; este cazul rigidului.
sunt perpendiculari,
ca in cazul a doua corpuri legate printr-un fir inextensibil, perfect
intins; este cazul rigidului.
In cazul rigidului, teorema energiei cinetice - forma diferentiala este:
![]() (158)
(158)
Variatia energiei cinetice in timpul elementar dt este egala cu lucrul mecanic elementar al fortelor care actioneaza asupra rigidului, efectuat in acelasi interval de timp.
Teorema energiei cinetice forma integrala (finita) se obtine prin integrarea formei diferentiale (158) in intervalul de timp (t0, t1).
![]() (159)
(159)
Variatia energiei cinetice din pozitia initiala in pozitia finala este egala cu lucrul mecanic al fortelor care actioneaza asupra rigidului, efectuat intre cele doua pozitii (in intervalul de timp t0,, t1).
Un sistem material este conservativ
daca fortele interioare sistemului deriva dintr-o functie
de forta ![]() , adica:
, adica:
![]() (160)
(160)
Daca
se introduce notiunea de energie potentiala, definita ca in
cazul punctului material ![]() atunci relatia (160)
devine:
atunci relatia (160)
devine:
![]() (161)
(161)
Introducand relatia (161) in (155) se obtine:
![]() (162)
(162)
Daca:
![]() (163)
(163)
care constituie teorema conservarii energiei mecanice:
Daca lucrul mecanic elementar al fortelor exterioare care actioneaza asupra unui sistem conservativ este nul intr-un interval de timp dat, energia mecanica a sistemului se conserva, adica este constanta in acel interval de timp sau un sistem conservativ inchis are energia mecanica constanta.
Cazul miscarii relative a sistemului material sau a rigidului in raport cu centrul de greutate (al maselor).
Cand originea sistemului mobil atasat rigidului
este centrul de greutate al acestuia ![]() , expresia energiei cinetice devine conform relatiei (116):
, expresia energiei cinetice devine conform relatiei (116):
![]()
care exprima teorema Koenig pentru energiea cinetica a rigidului in miscare fata de un reper fix.
Tot in acest caz, lucrul
mecanic elementar al sistemului de
forte ![]() , conform (90) este:
, conform (90) este:
![]()
Teorema
energiei cinetice, conform (158) este ![]() si care prin
diferentiere conduce la:
si care prin
diferentiere conduce la:
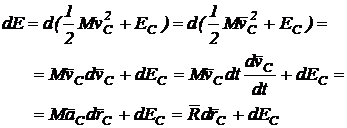 (164)
(164)
Introducand expresiile (90) si (164) in (158) rezulta:
![]() (165)
(165)
care exprima teorema energiei cinetice din miscarea rigidului in raport cu centrul de greutate.
Variatia energiei cinetice a rigidului in miscarea fata de centrul de greutate, in timpul elementar dt este egala cu lucrul mecanic elementar al fortelor exterioare care actioneaza asupra rigidului, efectuat in acelasi interval de timp.
Teorema energiei cinetice pastreaza aceeasi forma in miscarea relativa fata de centrul de greutate ca si in miscarea fata de un punct fix
Daca
fortele care actioneaza asupra rigidului sunt conservative,
adica deriva dintr-o functie de forta ![]() :
:
![]() (166)
(166)
Folosind
notiunea de energie potentiala ![]() , relatia (166) devine:
, relatia (166) devine:
![]() (167)
(167)
Introducand relatia (167) in (165) se obtine:
![]() (168)
(168)
Daca fortele care actioneaza asupra unui rigid sunt forte conservative, energia mecanica a rigidului in miscarea relativa fata de centrul de greutate se conserva, adica are o valoare constanta care se determina din conditiile initiale ale miscarii
Observatie. Teoremele impulsului, momentului cinetic si energiei cinetice se aplica numai cu vitezele absolute.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1322
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved