| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Rezolvarea numerica a siustemelor de ecuatii neliniare
Tematica lucrarii: 1. Generalitati;
2. Rezolvarea sistemelor neliniare prin metoda lui Newton-Raphson;
3. Probleme de rezolvat;
4. Concluzii.
1. Generalitati
Un sistem de ecuatii neliniare poate fi pus sub forma generala:
f(x) = 0 (1)
unde f(x) este o functie vectoriala, avand componentele f (x), f (x),,fn(x), x este vectorul solutiei cautate x = (x ,x ,,x ), iar 0 este vectorul nul. Ca si in cazul ecuatiilor neliniare cu o necunoscuta, rezolvarea numerica se face prin metode iterative, pornind de la o valoare initiala data a vectorului solutie. Metodele de rezolvare numerica pot fi aplicate si sunt convergente numai in cadrul unui interval (multidimensional in cazul sistemelor de ecuatii), in care solutia exista si este unica. Convergenta solutiei aproximative este stabilita prin teoreme corespunzatoare anumitor tipuri de probleme, in cadrul analize numerice.
2. Rezolvarea sistemelor neliniare prin metoda lui Newton-Raphson
Metoda
Newton-Raphson generalizeaza metoda tangentei (lui
f (x ,x ,,xn
f (x ,x ,,xn (2)
fn(x ,x ,,xn
unde fi(x ,x ,,xn (i = 1,2,,n) sunt functii cu variabila vectoriala si reprezinta ecuatiile neliniare cu toti termenii trecuti in partea stanga. In forma compacta sistemul de ecuatii neliniare poate fi scris ca mai sus:
f(x) = 0 (3)
unde: 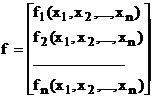
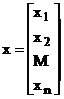 (4)
(4)
Se
poate arata ca folosind notatia matriceala, formalismul
metodei lui
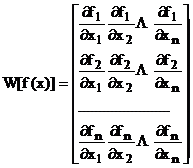 (5)
(5)
Calculul inversei derivatei scalare prin impartire este inlocuit de inversarea matricei W[f(x)], iar inmultirea de produsul matriceal (aplicatia matricei W [f(x)] asupra vectorului f(xk
Astfel solutia aproximativa obtinuta la fiecare pas de iteratie este data de ecuatia recursiva vectoriala:
xk+ xk - W [f(xk)] f(xk (6)
Mentionam ca si in cazul vectorial se pot da interpretari geometrice caracteristice dar acestea sunt specifice elementelor spatiului multidimensional.
3. Probleme de rezolvat
Rezolvarea unui sistem de ecuatii neliniare (de gradul doi)
In vederea realizarii unui program MathCad pentru rezolvarea unui sistem de ecuatii neliniare prin metoda Newton-Raphson, consideram exemplul urmator. Fie sistemul neliniar de doua ecuatii cu doua necunoscute:
x2 + y (7)
x + 2y = 1
Pentru rezolvarea numerica iterativa consideram valoroile initiale:
x0 = 1 ; y (8)
Metoda lui Newton-Raphson presupune scrierea sistemului sub forma:
f (x,y) = 0 unde: f (x,y) = x + y (9)
f (x,y) = 0 f (x,y) = x + 2y - 1
In limbaj MathCad pentru cele doua functii de cate doua variabile, f (x,y) si f (x,y) utilizam notatiile f1(x,y) si f2(x,y) deoarece notatia cu indice are alta semnificatie.
Programul MathCad este capabil sa calculeze derivatele partiale, definite sub forma simbolica. Acestea vor fi notate conform pozitiei in matricea iacobiana W(f(x)) prin df11(x,y), df12(x,y), df21(x,y) si df22(x,y) . Rezulta relatiile de definitie:
![]()
![]() (10)
(10)
![]()
![]() (11)
(11)
Pentru determinarea ecuatiei vectoriale recursive utilizate pentru aproximarea solutiei, definim in limbaj MathCad matricea iacobiana W(z) si vectorul corespunzator sistemului de ecuatii:
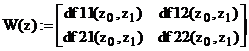
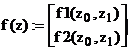
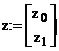 (12)
(12)
unde variabila z = (z ,z ) = (x,y) reprezinta vectorul solutie asociat necunoscutelor x si y.
Acum poate fi definita (in MathCad) ecuatia vectoriala recursiva pentru aproximarea solutiei:
![]() (13)
(13)
Inainte de scrierea ecuatiei trebuie definit modul de variatie a lui k si valoarea initiala pentru vectorul solutie z . Aceasta trebuie aleasa suficient de aproape de solutia exacta, astfel incat procesul iterativ sa fie convergent (in acest caz s-au ales valori unitare
k
:= 0..N ![]() (14)
(14)
Se cere:
Implementarea algoritmilor de rezolvare in limbaj MathCad;
Stabilirea numarului de iteratii pana la stabilizarea solutiei aproximative;
Comparatia cu solutia calculata iterativ, utilizand rezolvitorul disponibil in cadrul programului MathCad.
Rezolvarea unui circuit electric neliniar
Aplicatie reductibila la rezolvarea unei ecuatii neliniare
Scopul acestei aplicatii este rezolvarea cu ajutorul programului MathCad a unei probleme din domeniul electrotehnic. Se considera un circuit electric continand o sursa de tensiune continua E, trei diode D1, D2, D3, conectate in paralel si o rezistenta de sarcina R (fig. 1).
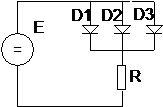 Fig.1. Circuitul
continand diodele D1, D2, D3
Fig.1. Circuitul
continand diodele D1, D2, D3
Acest circuit modeleaza un redresor monoalternanta de curent intens, care utilizeaza diode cu curenti nominali de valori mai mici decat este necesar sarcinii. Intr-o situatie reala sursa de tensiune este evident alternativa. Dar scopul aplicatiei de fata este analiza distribiutiei de curent prin cele trei diode, atunci cand acestea au caracteristici (neliniare) diferite. Pentru aceasta situatie poate fi folosita o sursa de tensiune continua. In acest circuit model s-au considerat valori reduse (scalate) ale parametrilor electrici. Astfel se alege:
E = 10 V si R = 10 (15)
Caracteristicile neliniare ale diodelor D1, D2, D3 sunt date sub forma unor dependente ale curentilor in functie de caderile de tensiune respective:
i = f1(u i = f (u i = f (u (16)
unde functiile f (u ), f (u ), f (u ) reprezinta dependenta neliniara fata de tensiuni dupa modelele exponentiale:
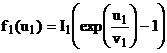
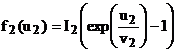
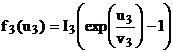 (17)
(17)
Valorile I , I , I , v , v , v reprezinta parametrii fiecarui model individual, iar u u u sunt caderile de tensiune respective. Se considera ca parametrii modelului diodei D1 sunt:
I = Is = 10 A v = vt = 0.025 V (18)
Celelalte doua diode au parametrii cu valori diferite, plasati in jurul valorilor corespunzatoare lui D1, cu o anumita toleranta tol = 0.03 , astfel:
![]()
![]() (19)
(19)
![]()
![]() (20)
(20)
Rezulta graficele caracteristicilor diodelor din figura 2.
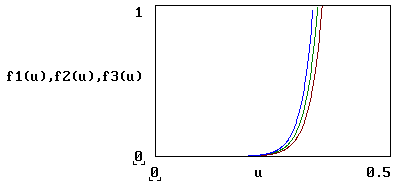
Fig. 2. Graficele caracteristicilor celor trei diode
In circuitul de mai sus se observa ca valoarea caderii de tensiune este aceeasi pentru toate cele trei diode, deci u = u = u = u . Astfel, conform teoremei a doua lui Kirchhoff, functionarea circuitului poate fi modelata matematic printr-o singura ecuatie neliniara, cu o singura necunoscuta 'u'. Daca u este determinat, curentii prin diode pot fi calculati usor cu ajutorul formulelor (39). Ecuatia de baza poate fi pusa sub forma anularii unei functii F(u):
F(u) = 0 (21)
unde ![]() (22)
(22)
si u este caderea de tensiune pe diode, iar paranteza reprezinta curentul prin rezistenta R.
Pentru rezolvarea iterativa a ecuatiei neliniare este necesara o valoare de pornire. Aceasta poate fi aleasa studiind graficul de variatie a functiei F(u) , prezentat in figura 3.
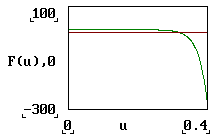 Fig. 3. Graficul de variatie a functiei F(u)
Fig. 3. Graficul de variatie a functiei F(u)
Se observa ca in intervalul studiat ecuatia are solutie unica. Pentru pornirea procesului iterativ se poate alege initiala u = 1. Pentru verificare s-a apelat si la procedura deja implementata in MathCad 'root'. Rezulta valoarea necunoscutei u:
u := root((F(u),u) => u = 0.316 (V) (23)
Pentru rezolvarea numerica s-au utilizat cele trei metode prezentate. Parametrii de iteratie alesi, pentru care s-a obtinut acelasi rezultat, identic cu cel de mai sus au fost:
- numarul de iteratii: N = 40 ;
- valoare unitara pentru pasul de pornire la metoda tangentei;
- interval de lucru = [0.3,0.4] pentru metoda coardei;
- interval de lucru = [0,2] pentru metoda bipartitiei
Apoi, pentru valorile curentilor prin diode s-au obtinut rezultatele:
i = 0.308 (A) i = 0.219 (A) i = 0.441 (A) (24)
Aplicatie modelata de un sistem de ecuatii neliniare
Se considera un circuit electric continand o sursa de tensiune continua E, doua diode D1, D2, conectate in paralel si o rezistenta de sarcina Rs (fig. 4).
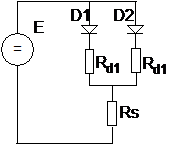 Fig.4. Circuitul continand diodele D1,
D2.
Fig.4. Circuitul continand diodele D1,
D2.
Modul de abordare al circuitului este similar cazului de mai sus, cu deosebirea ca, de data aceasta modelele matematice corespunzatoare diodelor contin cate o dioda ideala (D1 si D2) si cate o rezistenta interna (Rd1 , Rd2 ). Pentru cele doua rezistente interne s-au considerat valorile urmatoare:
Rd1 5 ![]() (25)
(25)
Sursa de alimentare si rezistenta de sarcina au aceleasi valori ca mai sus. De asemenea functiile care descriu neliniaritatile diodelor si parametrii acestora sunt aceleasi ca mai sus.
Pentru deducerea ecuatiilor de functionare, se observa ca cei doi curenti prin diode sun determinati de functiile f1(u ) si f (u ). Caderile de tensiune pe cele doua diode ideale, conform cu teorema a doua a lui Kirchhoff, sunt date de relatiile urmatoare:
tensiunea
pe dioda D1 = ![]() (26)
(26)
tensiunea
pe dioda D2 = ![]() (27)
(27)
Expresia: ![]() reprezinta
caderea de tensiune pe rezistenta de sarcina Rs, iar produsele:
reprezinta
caderea de tensiune pe rezistenta de sarcina Rs, iar produsele: ![]() si
si ![]() reprezinta
caderile de tensiune pe rezistentele interne ale celor doua
diode. Rezulta sistemul de ecuatii neliniare caracteristice
circuitului, care poate fi scris sub forma:
reprezinta
caderile de tensiune pe rezistentele interne ale celor doua
diode. Rezulta sistemul de ecuatii neliniare caracteristice
circuitului, care poate fi scris sub forma:
F1(i ,i F (i ,i (28)
unde ![]() (29)
(29)
![]() (30)
(30)
Pentru rezolvarea sistemului neliniar se aplica metoda lui Newton-Raphson, descrisa mai sus.
S-a considerat un numar de N = 400 iteratii si o conditie initiala nenula pentru vectorul curentilor:
![]() (31)
(31)
In urma calculelor efectuate cu ajutorul programului MathCad, rezulta pentru valorile curentilor:
i = 0.392 (A) i = 0.379 (A) (32)
Pentru estimarea erorilor de aproximare a solutiei, se verifica daca solutia aproximativa, dupa efectuarea celor N iteratii, duce la anularea (in sens aproximativ) a ecuatiilor sistemului neliniar. Rezulta:
F(i<N> F(i<N> (33)
Se cere:
* Implementarea algoritmilor de rezolvare in limbaj MathCad;
* Stabilirea numarului de iteratii pana la stabilizarea solutiei aproximative;
* Comparatia cu solutia calculata iterativ, utilizand rezolvitorul disponibil in cadrul programului MathCad.
4. Concluzii
Spre deosebire de ecuatiile neliniare, rezolvarea numerica a sistemelor de ecuatii este mai dificila, datorita formularii mai complicate a conditiilor de existenta si unicitate a solutiei, pe de o parte, si datorita problemelor de convergenta, pe de alta parte;
Un handicap serios in rezolvarea acestui tip de probleme este imposibilitatea sau dificultatea unei reprezentari grafice care sa permita controlul conditiilor impuse si a procesului iterativ insasi.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3692
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved