| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Consistenta si consecinte (deductii din ipoteze)
1. Definitie. O multime de
propozitii S![]() S(Q)
se numeste consistenta
daca exista o valorizare v
pe S(Q) astfel incat orice propozitie
S(Q)
se numeste consistenta
daca exista o valorizare v
pe S(Q) astfel incat orice propozitie ![]() sa fie
adevarata in raport cu v;
in caz contrar S se numeste inconsistenta.. In particular, daca S
sa fie
adevarata in raport cu v;
in caz contrar S se numeste inconsistenta.. In particular, daca S![]() atunci spunem ca
atunci spunem ca ![]() , in loc de
, in loc de ![]() , este consistenta respectiv inconsistenta. O
valorizare v se numeste interpretare a lui S daca orice propozitie
, este consistenta respectiv inconsistenta. O
valorizare v se numeste interpretare a lui S daca orice propozitie ![]() este adevarata
in raport cu v. Notam cu Int(S} multimea tuturor
interpretarilor lui S. Astfel S este consistenta daca si numai
daca Int(S}
este adevarata
in raport cu v. Notam cu Int(S} multimea tuturor
interpretarilor lui S. Astfel S este consistenta daca si numai
daca Int(S}![]() si inconsistenta
daca si numai daca Int(S}
si inconsistenta
daca si numai daca Int(S}![]() .
.
Multimea de propozitii S se numeste falsificabila daca exista o valorizare v astfel incat orice propozitie ![]() sa fie falsa
in raport cu v; in particular o
propozitie
sa fie falsa
in raport cu v; in particular o
propozitie ![]() se numeste
falsificabila daca
se numeste
falsificabila daca ![]() este falsificabila.
este falsificabila.
2. Teorema. Fie ![]() S(Q) o propozitie.
S(Q) o propozitie.
(a) ![]() este consistenta
daca si numai daca
este consistenta
daca si numai daca ![]() este
falsificabila.
este
falsificabila.
(b) ![]() este tautologie
daca si numai daca
este tautologie
daca si numai daca ![]() este
contradictie.
este
contradictie.
Demonstratie. Fie v o valorizare arbitrara. Avem ![]() si, deoarece
si, deoarece ![]() si
si ![]() , rezulta
, rezulta ![]() daca si
numai daca
daca si
numai daca ![]() ceea ce
demonstreaza afirmatia de la (a). Afirmatia de la (b) este de
asemenea evidenta.
ceea ce
demonstreaza afirmatia de la (a). Afirmatia de la (b) este de
asemenea evidenta.
3. Definitie. Teorema 2. furnizeaza o metoda de dmonstratie in
logica numia demonstratie
prin respingere si anume in loc sa se demonstreze ca o
propozitie ![]() este consistenta
sau tautologie se demonstreaza ca
este consistenta
sau tautologie se demonstreaza ca ![]() este
falsificabila respectiv contradictie. In acest moment metoda poate parea
puerila dar se va dovedi ca in practica ea este foarte eficienta.
este
falsificabila respectiv contradictie. In acest moment metoda poate parea
puerila dar se va dovedi ca in practica ea este foarte eficienta.
4. Exemplu. Multimea
de propozitii ![]() este inconsistenta. Intr-adevar, fie v o valorizare oarecare. Presupunem
este inconsistenta. Intr-adevar, fie v o valorizare oarecare. Presupunem ![]() . Atunci
. Atunci
![]()
ceea
ce implica ![]() deci
deci ![]() si
si ![]() . Rezulta:
. Rezulta:
![]() .
.
Astfel
nu exista nici o valorizare v in
raport cu care toate propozitiile din ![]() sa fie
adevarate.
sa fie
adevarate.
Propozitia urmatoare da o lisa de proprietati ale entitatilor definite mai sus care sunt evidente motiv pentru care nu vom mai expune si demonstratia lor .
5. Propozitie. Fie S o multime de propoziti
si ![]() S(Q)
Avem:
S(Q)
Avem:
(a) Daca
S este consistenta atunci multimea ![]() este de asemenea
consistenta.
este de asemenea
consistenta.
(b)
Daca S este consistenta si ![]() este tautologie atunci
multimea
este tautologie atunci
multimea ![]() este de asemenea
consistenta.
este de asemenea
consistenta.
(c) Daca S este
inconsistenta atunci ![]() este de asemenea inconsistenta.
este de asemenea inconsistenta.
(d) Daca S este inconsistenta atunci ![]() este de asemenea
inconsistenta.
este de asemenea
inconsistenta.
6. Definitie. Fie S![]() S(Q)
o multime de propozitii. O propozitie oarecare
S(Q)
o multime de propozitii. O propozitie oarecare ![]() S(Q) se numeste consecinta
a lui S daca pentru orice interpretare
v a lui S avem
S(Q) se numeste consecinta
a lui S daca pentru orice interpretare
v a lui S avem ![]() ( adica daca toate propozitiile din S sunt adevarate in raport cu v atunci si
( adica daca toate propozitiile din S sunt adevarate in raport cu v atunci si ![]() este
adevarata in raport cu v si
in aceasta situatie scriem S
este
adevarata in raport cu v si
in aceasta situatie scriem S![]()
![]() . Putem privi S
ca o multime de ipoteze si consecintele
. Putem privi S
ca o multime de ipoteze si consecintele ![]() ale lui S ca propozitii care pot fi deduse din
aceste ipoteze. Multimea tuturor consecintelor lui S se
va nota cu Con(S).
ale lui S ca propozitii care pot fi deduse din
aceste ipoteze. Multimea tuturor consecintelor lui S se
va nota cu Con(S).
Propozitie. Fie ![]() S(Q) o multime finita de
propozitii. Avem
S(Q) o multime finita de
propozitii. Avem ![]() daca si
numai daca
daca si
numai daca ![]() .
.
Demonstratie.
Afirmatia rezulta deoarece pentru orice valorizare v avem ![]() daca si
numai daca
daca si
numai daca ![]() .
.
8. Exemple triviale. Daca ![]() , multimea vida, atunci, evident, o propozitie
, multimea vida, atunci, evident, o propozitie ![]() este
consecinta a lui S daca si numai daca
este
consecinta a lui S daca si numai daca ![]() este tautologie.
Astfel daca notam cu Taut
multimea tuturor tautologiilor din S(Q)
avem:
este tautologie.
Astfel daca notam cu Taut
multimea tuturor tautologiilor din S(Q)
avem: ![]() sau altfel spus pentru
o propozitie
sau altfel spus pentru
o propozitie ![]() avem:
avem:
![]() daca si
numai daca
daca si
numai daca ![]() este tautologie.
este tautologie.
De
obicei in loc de ![]() scriem
scriem ![]() . De asemenea este evident ca pentru orice multime
de propozitii S si orice
tautologie
. De asemenea este evident ca pentru orice multime
de propozitii S si orice
tautologie ![]() avem S
avem S![]()
![]() sau, altfel spus, pentru orice multime de
propozitii S avem
sau, altfel spus, pentru orice multime de
propozitii S avem 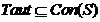 . Ca un alt exemplu
trivial mentionam ca pentru orice multime de
propozitii S avem
. Ca un alt exemplu
trivial mentionam ca pentru orice multime de
propozitii S avem ![]() sau,altfel spus,
daca
sau,altfel spus,
daca ![]() atunci S
atunci S![]()
![]() .
.
9. Exemplu. Avem:
![]()
![]()
![]() .
.
Intr-adevar
fie v o valorizare astefel incat ![]() . Deoarece propozitia
. Deoarece propozitia ![]() este
adevarata in raport cu valorizarea v rezulta ca A si
B sunt ambele adevarate in
raport cu v adica
este
adevarata in raport cu valorizarea v rezulta ca A si
B sunt ambele adevarate in
raport cu v adica 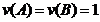 . Daca presupunem, prin absurd,
. Daca presupunem, prin absurd, ![]() , rezulta
, rezulta
![]() ,
,
o
contradictie. Astfel ![]() si C este o consecinta a celor doua
propozitii
si C este o consecinta a celor doua
propozitii ![]() si
si ![]() .
.
10. Propozitie. Fie ![]() S(Q). Avem:
S(Q). Avem:
(a) Daca ![]() atunci
atunci ![]() si
si ![]() .
.
(b) ![]() .
.
(c) ![]() S(Q)
S(Q)![]() pentru orice
pentru orice ![]() .
.
Demonstratie. (a) Fie ![]() . Pentru orice
. Pentru orice ![]() avem, deoarece
avem, deoarece ![]() ,
, ![]() deci
deci ![]() ; astfel
; astfel ![]() . Acum fie
. Acum fie ![]() . Fie v o
interpretare a lui
. Fie v o
interpretare a lui ![]() . Atunci, pentru orice
. Atunci, pentru orice ![]() , avem
, avem ![]() si, in
particular,
si, in
particular, ![]() ; astfel
; astfel ![]() .
.
(b) Deoarece ![]() avem, conform lui (a),
avem, conform lui (a),
![]() . Reciproc, fie
. Reciproc, fie ![]() si v o interpretare a lui S:
si v o interpretare a lui S: ![]() ; atunci
; atunci ![]() pentru orice
pentru orice ![]() ceea ce implica
ceea ce implica ![]() . Astfel
. Astfel ![]() si deci
si deci ![]() si
si ![]() .
.
(c) Evident.
11. Teorema( Teorema
Deductiei pentru consecinte). Fie S o multime de propozitii si ![]()
![]() S(Q). Avem
S(Q). Avem
S![]()
![]() daca si numai daca S
daca si numai daca S![]()
![]() .
.
Demonstratie. Presupunem ca S![]()
![]() si fie v
o valorizare astfel incat
si fie v
o valorizare astfel incat ![]() pentru orice
pentru orice ![]() . Daca
. Daca ![]() atunci v este o interpretare a lui S
atunci v este o interpretare a lui S![]() si, conform ipotezei,
si, conform ipotezei,![]() . Astfel
. Astfel
![]() ;
;
si S![]()
![]() .
.
Reciproc presupunem ca S![]()
![]() si fie v
o interpretare a lui S
si fie v
o interpretare a lui S![]() . Atunci in particular, v este o interpretare a lui S
si deci
. Atunci in particular, v este o interpretare a lui S
si deci ![]() . Daca presupunem ca
. Daca presupunem ca ![]() rezulta
rezulta
![]()
ceea
ce implica, ![]() si concluzia S
si concluzia S![]()
![]() este evidenta.
este evidenta.
12. Corolar. Fie n un numar intreg
pozitiv si ![]() S(Q)
S(Q)
Urmatoarele afirmatii sunt echivalente:
a) ![]() ;
;
b) Propozitia
![]() este o tautologie;
este o tautologie;
c)
Propozitia ![]() este o tautologie.
este o tautologie.
Demonstratie. a)![]() b) Inductie dupa n. Pentru
b) Inductie dupa n. Pentru ![]() avem, conform Teoremei
10,
avem, conform Teoremei
10, ![]() daca si
numai daca
daca si
numai daca ![]() si deci
si deci ![]() daca si
numai daca
daca si
numai daca ![]() este o tautologie.
Presupunem
este o tautologie.
Presupunem ![]() . Conform Teoremei 10.,
. Conform Teoremei 10.,
![]()
daca si numai daca
![]()
![]()
![]()
si,
conform ipotezei de inductie, ![]()
![]()
![]() daca si
numai daca
daca si
numai daca ![]() este tautologie.
este tautologie.
b)![]() c) Conform Propozitiei 7, avem
c) Conform Propozitiei 7, avem ![]() daca si
numai daca
daca si
numai daca ![]() si, conform
Teoremei 11.,
si, conform
Teoremei 11., ![]() daca si
numai daca propozitia
daca si
numai daca propozitia ![]() este o tautologie.
este o tautologie.
Exercitii
1. Demonstrati , folosind metoda tablelor de adevar, ca multimea de propozitii
S![]()
![]()
este consistenta si determinati toate interpretarile lui S.
2. Demonsrati
ca ![]() .
.
3.Fie S![]() .Aratati ca propozitia
.Aratati ca propozitia
![]()
nu este consecinta a lui S.
4. Fie S![]() , S
, S![]() doua multimi de propozitii.
Aratati ca
doua multimi de propozitii.
Aratati ca
a) ![]() ,
,
b) ![]() .
.
Atat la a) cat si la b) studiati incluziunea inversa si, in caz ca aceasta nu este adevarata, dati un contraexemplu.
5. Fie S o multime de propozitii
consistenta si ![]() o propozitie
arbitrara. Aratati ca multimea
o propozitie
arbitrara. Aratati ca multimea ![]() este
inconsistenta daca si numai daca
este
inconsistenta daca si numai daca ![]() .
.
6. Stabiliti daca urmatoarele propozitii din limbajul cotidian pot fi sau nu simultan adevarate:
(a) Martorul era speriat sau, daca John s-a sinucis atunci s-a gasit o scrisoare.
Daca martorul era speriat atunci John s-a sinucis.
(b) Dragostea este oarba si fericirea este la indemana sau, dragostea este oarba si femeile sunt mai inteligente dacat barbatii.
Daca fericirea este la indemana atunci dragostea nu este oarba.
Femeile nu sunt mai inteligente decat barbatii.
O multime de propozitii S se mumeste maximal consistenta daca este consistenta si
pentru orice multime de propozitii ![]() consistenta
astfel incat
consistenta
astfel incat ![]() avem
avem ![]() . Fie S o
multime de propozitii. Aratati ca multimea S este maximal consistenta
daca si numai daca pentru orice propozitie
. Fie S o
multime de propozitii. Aratati ca multimea S este maximal consistenta
daca si numai daca pentru orice propozitie ![]() avem
avem ![]() sau
sau ![]() .
.
Rezolvari
1. Construim simultan tablele de adevar ale celor doua propozitii:
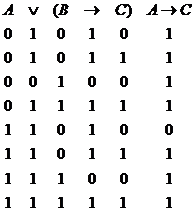
Interpretarile lui S sunt toate valorizarile v corespunzatoare liniilor 1, 2, 4, 6, 7, 8.
2. Rezulta
din tablele de adevar de mai jos. Aici interpretarile lui ![]() apar pe liniile 3, 4,
7 si 8 si rezultatele de pe coloana 8 arata ca in raport
cu toate aceste interpretari
propozitia
apar pe liniile 3, 4,
7 si 8 si rezultatele de pe coloana 8 arata ca in raport
cu toate aceste interpretari
propozitia ![]() este
adevarata.
este
adevarata.
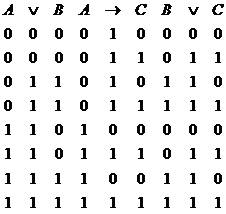
3. Problema
revine la a gasi printre cele 16 valorizari posibile ale atomilor A, B,
C, D una in raport cu care toate propozitiile din S sunt adevarate in timp ce ![]() nu este
adevarata. Luam
nu este
adevarata. Luam ![]() si
si ![]() si avem
si avem
![]()
![]() si
si ![]() avem, conform
Propozitiei 9.(a),
avem, conform
Propozitiei 9.(a), ![]() si
si ![]() . Deci
. Deci
![]() .
.
Incluziunea inversa nu este adevarata dupa cum arata urmatorul cuntraexemplu: luam
![]() ,
, ![]() si avem :
si avem :
(1)
![]() ,
,
(2)
![]()
Pentru
a demonstra (1) consideram o valorizare oarecare v astfel incat ![]() si
si ![]() . Avem
. Avem
![]()
si,
deoarece ![]() , rezulta
, rezulta ![]() ceeace
demonstreaza ca
ceeace
demonstreaza ca ![]() .Pentru a demonstra (2) alegem o valorizare v astfel incat
.Pentru a demonstra (2) alegem o valorizare v astfel incat ![]() si
si ![]() si avem ca
si avem ca ![]() si o alta
valorizare w astfel incat
si o alta
valorizare w astfel incat ![]() ; avem
; avem
![]()
si
astfel ![]() deci
deci ![]() .
.
b) Avem ![]() si
si ![]() ceea ce implica
ceea ce implica ![]() si
si ![]() deci
deci ![]() . Incluziunea inversa nu este adevarata
dupa cum arata urmatorul contraexemplu: luam
. Incluziunea inversa nu este adevarata
dupa cum arata urmatorul contraexemplu: luam ![]() si
si ![]() cu
cu ![]() . Avem
. Avem ![]() . Pe de alta parte avem, evident
. Pe de alta parte avem, evident ![]()
![]() si
si ![]() nu este tautologie.
nu este tautologie.
5. Presupunem ![]() inconsistenta si fie v o valorizare astfel incat
inconsistenta si fie v o valorizare astfel incat ![]() pentru orice
pentru orice ![]() . Deoarece multimea
. Deoarece multimea ![]() este
inconsistenta avem
este
inconsistenta avem ![]() deci
deci ![]() si
si ![]() . Reciproc, presupunem
. Reciproc, presupunem ![]() si fie v o valorizare oarecare. Daca
exista
si fie v o valorizare oarecare. Daca
exista ![]() astfel incat
astfel incat ![]() atunci
atunci ![]() este
inconsistenta. In caz contrar avem, deoarece
este
inconsistenta. In caz contrar avem, deoarece ![]() ,
, ![]() deci
deci ![]() ceea ce arata de
asemenea ca multimea
ceea ce arata de
asemenea ca multimea ![]() este
inconsistenta.
este
inconsistenta.
6. (a) Notam:
![]() Martorul era
speriat.,
Martorul era
speriat., ![]() John s-a
sinucis.
John s-a
sinucis. ![]() S-a gasit o
scrisoare.
S-a gasit o
scrisoare.
si
problema cere sa stabilim daca multimea ![]()
![]() este consistenta.
Putem vedea, din urmatoarea tabla de adevar, care sunt toate interpretarile acestei
multimi:
este consistenta.
Putem vedea, din urmatoarea tabla de adevar, care sunt toate interpretarile acestei
multimi:
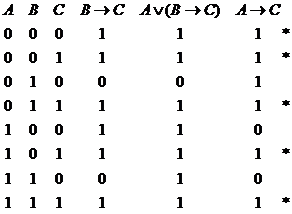
Interpretarile
multimii ![]() sunt cele
corespunzatoare liniilor marcate cu
sunt cele
corespunzatoare liniilor marcate cu ![]() .
.
(b) Notam:
![]() Dragostea este
oarba.
Dragostea este
oarba. ![]() Fericirea este la
indemana.
Fericirea este la
indemana.
![]() Femeile sunt mai inteligente decat barbatii.
Femeile sunt mai inteligente decat barbatii.
si
problema cere de fapt sa decidem daca multimea ![]() este sau nu
consistenta. Tabla de adevar este
este sau nu
consistenta. Tabla de adevar este
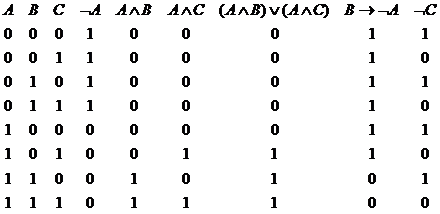
Tabla
arata, evident, ca pentru orice valorizare v exista o propozitie ![]() astfel incat
astfel incat ![]() si deci ca
multimea S este inconsistenta.
si deci ca
multimea S este inconsistenta.
Presupunem S maximal consistenta si fie ![]() S(Q). Deoarece S este
consistenta exista o valorizare v
astfel incat
S(Q). Deoarece S este
consistenta exista o valorizare v
astfel incat ![]() pentru orice
pentru orice ![]() . Avem
. Avem ![]() . Daca
. Daca ![]() atunci din
atunci din ![]() lui S rezulta
ca multimea
lui S rezulta
ca multimea ![]() este inconsistenta si deci
este inconsistenta si deci ![]() ceea ce implica
ceea ce implica ![]() . Astfel
. Astfel ![]() si multimea
si multimea ![]() este consistenta.
este consistenta. ![]() lui S implica
lui S implica ![]() si deci
si deci ![]() . Reciproc, presupunem ca pentru orice propozitie
. Reciproc, presupunem ca pentru orice propozitie ![]() avem
avem ![]() sau
sau ![]() si fie
si fie ![]() o multime de
propozitii consistenta astfel incat
o multime de
propozitii consistenta astfel incat ![]() . Fie
. Fie ![]() . Presupunem, prin absurd, ca
. Presupunem, prin absurd, ca ![]() . Prin ipoteza avem
. Prin ipoteza avem ![]() . Astfel
. Astfel ![]() . Deoarece
. Deoarece ![]() este consistenta,
exista o valorizare v astfel incat
este consistenta,
exista o valorizare v astfel incat
![]() pentru orice
pentru orice ![]() si, in
particular,
si, in
particular, ![]() ceea ce este o
contradictie.
ceea ce este o
contradictie.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2552
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved