| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Alte repere, alte sisteme de coordonate in E3
1. Coordonate polare in plan
Consideram
ca in spatiul punctual euclidian E2 avem reperul cartezian ![]() pe care-l mai notam
xOy. Prin fixarea reperului avem bijectia unic determinta:
pe care-l mai notam
xOy. Prin fixarea reperului avem bijectia unic determinta: ![]() .
.
Definitia 6.4. Se numeste reper polar plan ansamblul ![]() unde O este un punct
fix din plan iar D
o dreapta orientata fixa din plan care contine punctul O. Punctul O se numeste
pol iar D
axa polara. Fie M un punct arbitrar din plan (fig.6.10) Notam
unde O este un punct
fix din plan iar D
o dreapta orientata fixa din plan care contine punctul O. Punctul O se numeste
pol iar D
axa polara. Fie M un punct arbitrar din plan (fig.6.10) Notam
![]()
Reperului polar (O, D) ii asociem reperul cartezian xOy luand Ox =D si Oy D (fig. 6.11)
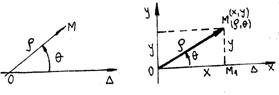
Fig.6.11
Din triunghiul OM1M rezulta relatiile
![]() (6.16)
(6.16)
Relatiile
(6.16) determina o corespondenta biunivoca intre multimile ![]() si
si ![]() daca
daca ![]() si
si ![]()
Perechea
![]() cu conditiile
cu conditiile ![]() constituie
coordonatele polare in plan ale punctului M ceea ce notam
constituie
coordonatele polare in plan ale punctului M ceea ce notam ![]() .
.
Originea
O are ![]() iar q
este nedeterminat.
iar q
este nedeterminat.
In
coordonate polare ecuatia ![]() (
(![]() fiind numar real constant >0) reprezinta un cerc de raza
fiind numar real constant >0) reprezinta un cerc de raza ![]() cu centrul in polul
O, iar
cu centrul in polul
O, iar ![]() reprezinta semidreapta
OM (fig.6.10). Pentru a gasi ecuatiile carteziene ale acestora pornind de la
ecuatiile lor polare (
reprezinta semidreapta
OM (fig.6.10). Pentru a gasi ecuatiile carteziene ale acestora pornind de la
ecuatiile lor polare (![]() ,
,![]() ) folosim inversele formulelor (6.16):
) folosim inversele formulelor (6.16):
![]() (6.17)
(6.17)
2. Coordonate semipolare in spatiu (cilindrice)
Consideram spatiul punctual euclidian E3 raportat la un reper cartezian Oxyz. Orice punct M I E3 este unic determinat de coordonatele sale carteziene.
Definitia 6.5. Se numeste reper semipolar in spatiu ansamblul unde P este un plan fix in care este un reper polar plan (fig. 6.12).
Fie M(x,y,z) IE*3 =E3 - axa Oz (fig.6.12). Notam
![]()
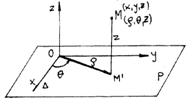
Fig.6.12
coordonatele polare in plan ale lui M', unde M' este proiectia lui M pe planul P.
Intre x,y,z si r q, z avem relatiile:
![]() (6.18)
(6.18)
Daca
impunem conditiile ![]() ,
, ![]() , atunci relatiile (6.24) determina o corespondenta biunivoca
intre tripletele (x,y,z)
, atunci relatiile (6.24) determina o corespondenta biunivoca
intre tripletele (x,y,z)![]() si (r q,
z)
si (r q,
z)![]() . Deci exista o corespondenta biunivoca si intre punctele
M(x,y,z) IE3
- axa Oz si tripletele (r q,
z)
. Deci exista o corespondenta biunivoca si intre punctele
M(x,y,z) IE3
- axa Oz si tripletele (r q,
z)![]() . Rezulta ca pozitia unui punct MIE*
poate fi caracterizata si de tripletul (r q,z)
cu conditiile
. Rezulta ca pozitia unui punct MIE*
poate fi caracterizata si de tripletul (r q,z)
cu conditiile ![]() ,
, ![]() . Numerele r q,
z se numesc coordonatele cilindrice ale punctului M.
. Numerele r q,
z se numesc coordonatele cilindrice ale punctului M.
Un
punct de pe Oz are ![]() determinat, iar q
este nedeterminat.
determinat, iar q
este nedeterminat.
Inversele formulelor (6.18) sunt
![]() (6.19)
(6.19)
Suprafetele de ecuatii
![]()
se numesc suprafetele coordonate ale reperului semipolar in spatiu (Fig.6.13)
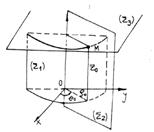
Fig.6.13
![]() reprezinta un cilindru
circular cu generatoarele paralele cu Oz.
reprezinta un cilindru
circular cu generatoarele paralele cu Oz. ![]() este semiplan a carui
prelungire contine axa Oz si
este semiplan a carui
prelungire contine axa Oz si ![]() este plan paralel cu
xOy fara punctul
este plan paralel cu
xOy fara punctul ![]() . In coordonate carteziene acestea au ecuatiile:
. In coordonate carteziene acestea au ecuatiile:
![]() (6.20)
(6.20)
3. Coordonate polare in spatiu (sferice)
Definitia 6.6. Se numeste reper polar in spatiu ansamblul format dintr-un punct fix O, o axa fixa D care trece prin O si un plan fix p ce trece prin D numit plan polar sau plan meridian principal.
Planul determinat de un punct PIE3 - axa D si D se numeste plan meridian al punctului P si il vom nota cu a. Unghiul diedru dintre planele a si p este determinat de unghiul q format de normalele duse in cele doua plane pe D. Notam :
![]() (fig.6.14).
(fig.6.14).
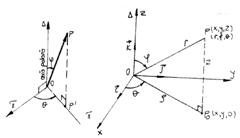
Fig.6.15
Reperului polar in spatiu ii asociem un reper cartezian Oxyz astfel: Oz =D, xOz =p, Oy p si orientata astfel incat Oxyz sa fie un reper drept (fig.6.15)
Din triunghiul OP0P se obtin relatiile
z = r![]() , OP0=r
, OP0=r![]() (6.21)
(6.21)
Proiectand pe OP0 pe Ox si Oy obtinem
![]() , (6.22)
, (6.22)
deci intre tripletele x,y,z si r, j q avem relatiile
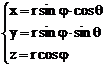 (6.23)
(6.23)
Din
(6.23) se observa ca unui triplet determinat ![]() ii corespunde un
singur punct M0 (x0, y0, z0) IE3.
ii corespunde un
singur punct M0 (x0, y0, z0) IE3.
Acelasi
punct M0 corespunde insa si tripletelor ![]() . Pentru a exista o corespondenta biunivoca intre punctele
spatiului E3 si tripletele ordonate
. Pentru a exista o corespondenta biunivoca intre punctele
spatiului E3 si tripletele ordonate ![]() trebuie sa stabilim
limitele de variatie pentru r, j
si q
trebuie sa stabilim
limitele de variatie pentru r, j
si q
Daca
impunem conditiile r>0, ![]() atunci formulele
(6.28) asigura o corespondenta biunivoca
intre multimile R-Oz si
atunci formulele
(6.28) asigura o corespondenta biunivoca
intre multimile R-Oz si ![]() , adica unui punct P
nesituat pe Oz ii corespunde un singur triplet
, adica unui punct P
nesituat pe Oz ii corespunde un singur triplet ![]()
![]() . In aceste conditii tripletul
. In aceste conditii tripletul ![]() constituie un sistem
de coordonate polare in spatiu(sferice). Punctele de pe Oz au q
nedeterminat iar pentru originea O coordonatele polare q
si j
sunt nedeterminate iar r=0. Din formulele (6.23) rezulta formulele inverse
constituie un sistem
de coordonate polare in spatiu(sferice). Punctele de pe Oz au q
nedeterminat iar pentru originea O coordonatele polare q
si j
sunt nedeterminate iar r=0. Din formulele (6.23) rezulta formulele inverse
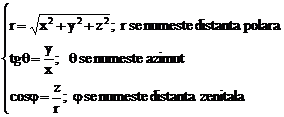 (6.24)
(6.24)
Coordonatele ![]() se numesc si
coordonate astronomice (Fig.6.16).
se numesc si
coordonate astronomice (Fig.6.16).
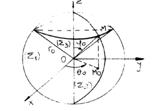
Fig.6.16
Suprafetele coordonate ale reperului polar in spatiu sunt
![]() sfera cu centrul in
origine mai putin polii;
sfera cu centrul in
origine mai putin polii;
![]() semiplan a carui
prelungire trece prin Oz;
semiplan a carui
prelungire trece prin Oz;
![]() semicon fara varf
(origine).
semicon fara varf
(origine).
In coordonate carteziene aceste ecuatii devin
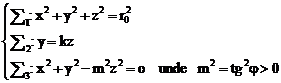 (6.25)
(6.25)
Comparand ecuatiile carteziene si cele polare (semipolare) ale suprafetelor coordonate in cazul reperului polar(respectiv semipolar) se observa ca cele din urma se scriu mult mai simplu decat ecuatiile carteziene. Concluzia este valabila si pentru alte suprafete. Ilustram aceasta afirmatie printr-un exemplu.
Fie
suprafata ![]() . In coordonate sferice
. In coordonate sferice ![]() deci
deci ![]() , iar
, iar 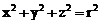 , deci
, deci ![]() sau
sau ![]() sau inca
sau inca ![]()
4. Coordonate omogene
Coordonate omogene in spatiu. Consideram in spatiul punctual E3 un reper cartezian Oxyz si un punct M de coordonate carteziene x,y,z( M(x,y,z)).
Definitia 6.7. Patru
numere reale X, Y, Z, T nesimultan nule (![]() ) se numesc coordonatele
omogene ale punctului M
) se numesc coordonatele
omogene ale punctului M
daca depind de x, y, z prin relatiile
![]() (6.26)
(6.26)
Din relatiile (6.26) rezulta ca daca (X,Y,Z,T) sunt coordonatele omogene ale punctului M atunci si (lX, lY, lZ, lT)( l 0) reprezinta acelasi punct. Daca luam T =1 obtinem coordonatele omogene (x,y,z,1) unde x,y,z sunt coordonatele carteziene ale punctului care se mai numesc coordonatele neomogene ale punctului M.
Daca
luam T=0, din conditia X2+Y2+T2 0
rezulta ca cel putin unul din numerele X,Y,Z este diferit de zero. Fie, de
exemplu X 0
si deci x =![]() , adica M(x,y,z) este un
punct de la infinit al spatiului. Ecuatia T =0 reprezinta ecuatia planului de la infinit al spatiului.
Punctele de la infinit ale axelor de coordonate Ox,Oy,Oz sunt respectiv
, adica M(x,y,z) este un
punct de la infinit al spatiului. Ecuatia T =0 reprezinta ecuatia planului de la infinit al spatiului.
Punctele de la infinit ale axelor de coordonate Ox,Oy,Oz sunt respectiv ![]() (1,0,0,0),
(1,0,0,0), ![]() (0,1,0,0),
(0,1,0,0), ![]() (0,0,1,0 ). Originea O(0,0,0,T), T
(0,0,1,0 ). Originea O(0,0,0,T), T
Coordonatele omogene au o importanta mare prin aceea ca ele permit studierea punctelor de la infinit ale figurilor geometrice si a proprietatilor figurilor geometrice in aceste puncte, folosind in acest studiu numai numere (coordonatele X,Y,Z,T) finite.
Exemple
1.
In coordonate omogene, ecuatia generala a planului, ax+by+cz+d =0, devine ![]() sau aX+bY +cZ +dT =0.
sau aX+bY +cZ +dT =0.
2. Curba plana
G: x3+y3-xy +2x -1=0 are ecuatia omogena
G: X3 +Y3-XYT +2XT2 -T3 =0. Aceasta ecuatie se obtine din ecuatia neomogena trecand la coordonatele omogene ale unui punct M(x,y) din planul xOy. In plan, coordonatele omogene sunt numerele reale X,Y,T nesimultan nule (X2+Y2+T2 0) care verifica relatiile
![]()
Pentru
a gasi punctele de la infinit (punctele improprii) ale curbei date
intersectam curba cu dreapta de la infinit a planului xOy adica cu dreapta de
ecuatie T =0. Obtinem astfel X3+Y3 =0, T =0TY=-X,
T=O, deci ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1433
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved