| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
CALCUL MATRICEAL
Reprezentarea matricei reale: ca o multime de m x n numere reale aranjate intr-un tablou dreptunghiular cu m linii si n coloane.
Notatie: Matricile se
noteaza cu litere mari A, B, C,.
sau A![]() A
A![]() , iar elementele lor se noteaza cu litere mici dublu
indexate
, iar elementele lor se noteaza cu litere mici dublu
indexate ![]() unde indicele i arata linia iar indicele j arata coloana pe care se afla elementul
unde indicele i arata linia iar indicele j arata coloana pe care se afla elementul ![]() (adeseori numit
element general sau generator al matricei A).
(adeseori numit
element general sau generator al matricei A).
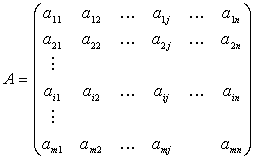
Pe scurt, se noteaza cu (![]() ), [
), [![]() ] sau ||
] sau ||![]() ||, mentionand multimea de valori pe care le pot
lua indicii i si j (de
exemplu
||, mentionand multimea de valori pe care le pot
lua indicii i si j (de
exemplu ![]() ,
, ![]() ).
).
A
= (![]() )
) ![]() ,
, ![]()
Definitia 1. Se spune ca matricea A este:
a) patrata (patratica), daca m = n;
b)
dreptunghiulara, daca ![]()
Definitia 2. Daca matricea A are m linii si n coloane atunci se spune ca aceasta este de ordinul m x n sau ca are dimensiunea m x n
Obs. Multimea matricelor m x n se noteaza de obicei cu:
M![]()
mentionand eventual daca
matricile sunt reale M![]() (R)
sau complexe M
(R)
sau complexe M![]() (C).
(C).
Definitia 3. Se spune ca A este:
matrice (vector) linie, daca m = 1 si n![]() 2;
2;
matrice (vector) coloana, daca m![]() 2 si n = 1.
2 si n = 1.
Definitia 4. Spunem ca o matrice este nula sau zero daca toate elementele ei sunt egale cu zero si se noteaza cu 0=(o).
Definitia 5. Spunem ca matricea patratica A este diagonala daca:
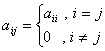
adica daca toate elementele ce nu apartin diagonalei principale sunt egale cu zero.
Exemplu:
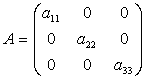
Definitia 6. Se spune ca A este matrice unitate de ordinul n daca:
![]()
Utilizand simbolul lui Kronecker
![]()
matricea unitate se poate scrie ca
![]() ,
, ![]() ,
, ![]()
Notatii utilizate: E, I sau U (eventual ![]() cand se
mentioneaza si dimensiunea).
cand se
mentioneaza si dimensiunea).
Definitia 7. Se spune ca A este superior triunghiulara daca toate elementele de sub diagonala principala sunt nule si ca este inferior triunghiulara daca toate elementele situate deasupra diagonalei sunt nule.
Exemplu:
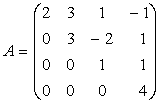 ,
, 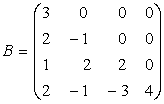
Definitia 8. Matricea patratica A este:
1) simetrica, daca
![]() ,
, ![]()
2) antisimetrica, daca ![]() ,
, ![]()
Exemplu:
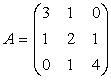 ,
, 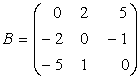
Matricea A este simetrica, iar B este antisimetrica.
Definitia 9. Se
spune ca matricile ![]() si
si ![]() sunt de acelasi tip sau ca au aceeasi
dimensiune daca ele au acelasi numar de linii si
acelasi numar de coloane.
sunt de acelasi tip sau ca au aceeasi
dimensiune daca ele au acelasi numar de linii si
acelasi numar de coloane.
Definitia 10. Doua matrice de acelasi tip ![]() si
si ![]() sunt egale si scriem
sunt egale si scriem ![]() daca toate
elementele lor sunt egale doua cate doua (adica
daca toate
elementele lor sunt egale doua cate doua (adica ![]() pentru toti i si j).
pentru toti i si j).
Exemple:
1. 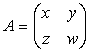 ,
, 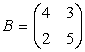
A=B ![]() si w = 5
si w = 5
2. 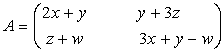 ,
, 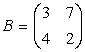
A = B ![]() ,
, ![]() ,
, ![]() ,
, ![]() , de unde deducem ca
, de unde deducem ca ![]() si
si ![]() .
.
Definitia 11. Se spune
ca intre matricile ![]() si
si ![]() de acelasi tip are loc relatia
de acelasi tip are loc relatia ![]() daca
daca ![]() pentru toti i si j.
pentru toti i si j.
Adunarea si scaderea a doua matrice
Definitia 12. Fiind date matricile ![]() si
si ![]() de acelasi tip se numeste suma a lor matricea
de acelasi tip se numeste suma a lor matricea ![]() ale carei elemente sunt:
ale carei elemente sunt:
![]() ,
, ![]() si
si ![]()
Asadar,
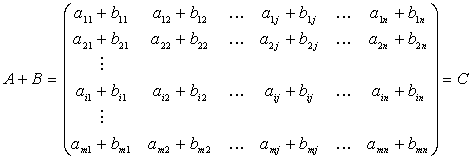
Definitia 13. Fiind date matricile ![]() si
si ![]() de acelasi tip se numeste diferenta a lor
matricea
de acelasi tip se numeste diferenta a lor
matricea ![]() ale carei elemente sunt:
ale carei elemente sunt:
![]() ,
, ![]() si
si ![]()
Exemplu:
Fie
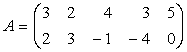 ,
, 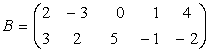
Avem
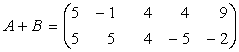 si
si 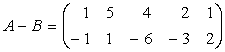
Propozitia 1. Adunarea matricelor are urmatoarele proprietati:
1) ![]() asociativa
asociativa
2) ![]() comutativa
comutativa
3) 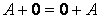
4) ![]()
Inmultirea unei matrice cu un numar (scalar)
Definitia 14. Fiind data matricea ![]() si scalarul
si scalarul ![]() R se numeste
produs al acestora matricea
R se numeste
produs al acestora matricea ![]() ale carei elemente sunt
ale carei elemente sunt
![]() ,
, ![]() ,
, ![]()
Teorema 1. Pentru orice matrice A si B de
acelasi tip si orice scalari ![]() si
si ![]() au loc
urmatoarele proprietati:
au loc
urmatoarele proprietati:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
Matricea ![]() se numeste opusa
matricei A.
se numeste opusa
matricei A.
Exemplu:
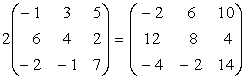
Inmultirea a doua matrice
Definitia 15. Fie ![]() o matrice m x n si
o matrice m x n si ![]() o matrice n x p. Se
numeste produs al matricelor A
si B (sau A cu B) matricea
o matrice n x p. Se
numeste produs al matricelor A
si B (sau A cu B) matricea ![]() ale carei
elemente
ale carei
elemente ![]() sunt:
sunt:
![]() ,
, ![]() ,
, ![]()
Conform
definitiei de mai sus, rezulta ca se inmultesc elementele
de pe linia i din matricea A cu elementele de pe coloana j din matricea B, "fiecare cu fiecare", se aduna produsele si rezultatul
obtinut constituie elementul ![]() , aflat deci pe linia i si coloana j in matricea produs C.
Pentru ca produsul
, aflat deci pe linia i si coloana j in matricea produs C.
Pentru ca produsul ![]() sa poata fi
efectuat trebuie ca numarul de coloane al matricei A sa fie egal cu numarul liniilor matricei B.
Remarcam ca daca A
este de tipul m x n iar B este de tipul n x p, atunci C este de tipul m x p. Este posibil ca daca
sa poata fi
efectuat trebuie ca numarul de coloane al matricei A sa fie egal cu numarul liniilor matricei B.
Remarcam ca daca A
este de tipul m x n iar B este de tipul n x p, atunci C este de tipul m x p. Este posibil ca daca ![]() poate fi
calculata se poate ca
poate fi
calculata se poate ca ![]() sa nu poata
fi calculata.
sa nu poata
fi calculata.
Exemple: 1) Fie
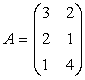 si
si
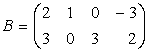
Avem deci ![]() M
M![]() si
si ![]() M
M![]() .Vom obtine prin inmultire o
matrice
.Vom obtine prin inmultire o
matrice ![]() M
M![]() astfel:
astfel:

Fie
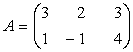 si
si 
Cum ![]() M
M![]() si
si ![]() M
M![]() rezulta matricea
rezulta matricea ![]() M
M![]() de forma:
de forma:
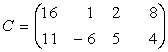
Definitia 16. Daca produsele ![]() si
si ![]() exista atunci se
spune ca:
exista atunci se
spune ca:
produsul este comutativ daca ![]() =
=![]() , iar A si B permutabile;
, iar A si B permutabile;
produsul este necomutativ daca ![]()
![]()
![]() .
.
Propozitia 2. Pentru orice matrice A, B, si C pentru care produsele de mai jos
exista si pentru orice scalar ![]() avem:
avem:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
![]()
![]() (in general)
(in general)
6) Daca ![]() =
=![]() atunci
atunci ![]() =
=![]() pentru orice p, q
pentru orice p, q![]() N
N
7) Daca A = 0 sau B = 0 atunci AB = 0 dar nu si reciproc.
8)![]() pentru orice matrice
patratica A
pentru orice matrice
patratica A
Exemple: 1) Fie
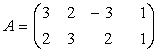 si
si 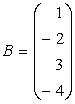
Cum ![]() M
M![]() si
si ![]() M
M![]()
![]()
![]() M
M![]()
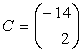
2) Fie ![]() si
si 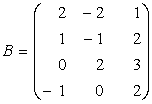
![]() M
M![]() si
si ![]() M
M![]()
Deci![]() M
M![]() -6 -2)
-6 -2)
Fie
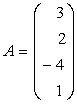 si B= (1 -2 -3)
si B= (1 -2 -3) ![]() M
M![]() si
si![]() M
M![]()
![]()
![]() M
M![]()
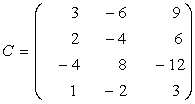
Transpunerea unei matrice
Definitia 17. Fiind data matricea ![]() se numeste
transpusa a acesteia si se noteaza cu
se numeste
transpusa a acesteia si se noteaza cu![]() ,
, ![]() ,
, ![]() ,
, ![]() sau
sau ![]() etc. matricea B ale carei elemente sunt
etc. matricea B ale carei elemente sunt ![]() =
= ![]() , pentru toti i
si j, adica:
, pentru toti i
si j, adica:
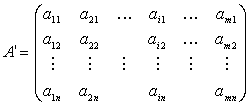
Exemplu:
Daca 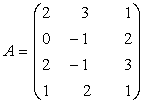 , atunci
, atunci 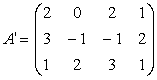
Se remarca ca daca ![]() atunci prin
transpunere se obtine matricea
atunci prin
transpunere se obtine matricea ![]() .
.
Propozitia 3.Pentru orice matrice A, B de acelasi tip
si pentru orice scalar ![]() sunt adevarate
urmatoarele proprietati:
sunt adevarate
urmatoarele proprietati:
1. ![]()
2. (![]() )
)![]() =
=![]()
![]()
3. ![]()
4. ![]()
5. Daca A este simetrica atunci ![]() si reciproc.
si reciproc.
3.5 Partitionarea matricilor
Definitia 18. Fiind data matricea ![]() ,
, ![]() ,
, ![]() , se numeste partitionare a acesteia
operatiunea de separare a liniilor sau a coloanelor sale printr-una sau
mai multe drepte orizontale sau verticale, conventional trasate, astfel incat
sa se obtina matrici de
dimensiuni mai mici.
, se numeste partitionare a acesteia
operatiunea de separare a liniilor sau a coloanelor sale printr-una sau
mai multe drepte orizontale sau verticale, conventional trasate, astfel incat
sa se obtina matrici de
dimensiuni mai mici.
Exemplu:
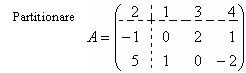
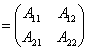
![]()
![]()
![]()

unde
![]() ,
, ![]() etc.
etc.
Definitia 19.
Fiind data matricea patrata ![]() , determinantul
sau se noteaza cu det A ,
sau |A| , fiind scris astfel:
, determinantul
sau se noteaza cu det A ,
sau |A| , fiind scris astfel:
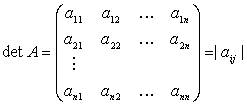
Definitia 20. Dezvoltarea determinantului dupa linia i
![]() ,
, ![]()
unde ![]() reprezinta
minorul (determinantul de ordin mai mic cu o unitate decat det A) care se obtine din det A suprimand linia i si coloana j.
reprezinta
minorul (determinantul de ordin mai mic cu o unitate decat det A) care se obtine din det A suprimand linia i si coloana j.
![]() Determinantul
Determinantul
![]() se numeste
complementul algebric al lui .
se numeste
complementul algebric al lui .
Definitia 21. Dezvoltarea determinantului det A dupa coloana j
![]() ,
, ![]()
Exemple: 1) Fie
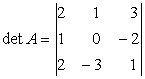 pe care il
calculam dupa linia intai.
pe care il
calculam dupa linia intai.
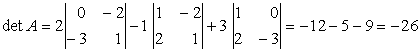
2) Dezvoltam acelasi determinant dupa coloana a doua.
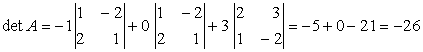
3) Calculam dupa linia intai determinantul de ordin patru
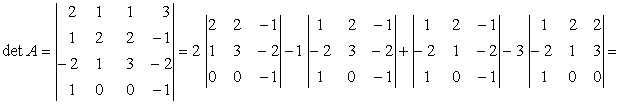
![]()
Propozitia 4. Urmatoarele afirmatii (proprietati) sunt adevarate intodeauna:
Determinantul nu se schimba prin transpunerea matricei
Daca se schimba intre cele doua linii (sau doua coloane) atunci determinantul isi schimba numai semnul
Daca matricea are doua linii (sau doua coloane) proportionale atunci determinantul este egal cu zero
Daca toate elementele unei linii (sau coloane) sunt nule, atunci determinantul este egal cu zero
Daca elementele unei linii (sau coloane) se inmultesc cu un numar, atunci determinantul se inmulteste cu acelasi numar
Daca la elementele unei linii (sau coloane) se aduna elementele altei linii (sau coloane) inmultite cu un numar, atunci determinantul matricei nu se schimba.
Propozitia 5. Daca A si B sunt matrici patrate de ordinul n atunci
![]()
Definitia 22.
Spunem ca matricea A este
nesingulara (sau regulata) daca ![]() . In caz contrar spunem ca A este singulara.
. In caz contrar spunem ca A este singulara.
Definitia 22. Se
spune ca matricea A este
inversabila daca exista o matrice de acelasi tip cu ea,
notata cu ![]() , astfel incat:
, astfel incat:
![]()
Observatie.
Daca exista, matricea ![]() se numeste
inversa matricei A si este
data de formula:
se numeste
inversa matricei A si este
data de formula:
![]() =
=![]()
unde
A* se numeste matricea
adjuncta a lui A si se
obtine din transpusa matricei A
inlocuind fiecare element al transpusei prin complementul sau algebric.
Analiza formulei de mai sus ne conduce la concluzia ca ![]() exista daca:
exista daca:
A este matrice patrata;
A
este nesingulara, adica ![]() .
.
Exemplu: Fie matricea
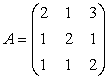
![]() , deci A este
nesingulara.
, deci A este
nesingulara.
Complementul
algebric va fi: ![]()
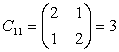 ,
, 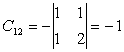 ,
, 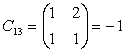
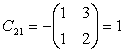 ,
, 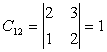 ,
, 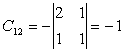
![]() ,
, ![]() ,
, ![]()
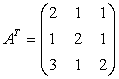
Inlocuim fiecare element al transpusei cu complementul sau algebric.
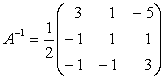 =
=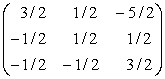
Pentru verificare va trebui ca ![]()
Exemplu: Fie matricea
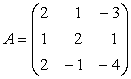 ;
; ![]()
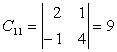 ,
, 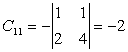 ,
, 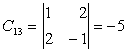
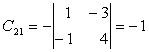 ,
, 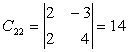 ,
, 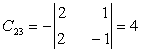
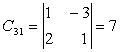 ,
, 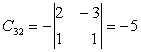 ,
, 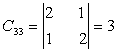
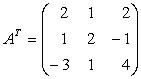
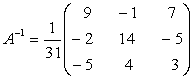
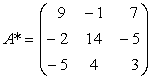
;
Propozitia 6. Daca A si B sunt matrici inversabile de acelasi ordin atunci:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Definitia 23. Fie A o matrice de ordin m x n. Se numeste rang al matricei A si se noteaza prin rang (A) ordinul maxim al minorului sau nenul.
Aceasta inseamna ca exista cel putin un minor al lui A de ordin r care este nenul si toti minorii lui A de ordin (r + 1) sunt nuli. Pentru determinarea rangului unei matrice procedam astfel:
pornind de la elementele matricei A , trecem de la minorii de ordin inferior la cei de ordin superior ;
prsupunand ca am gasit minorul nenul M de ordin r, calculam toti minorii de ordin r + 1 obtinuti din M prin bordare cu o linie si o coloana. Daca toti acesti minori sunt nuli, rangul este r iar daca macar unul este nenul, atunci se reia procedeul pentru noul minor nenul.
Exemplu: Fie

Consideram
minorul de ordin 2, 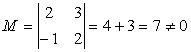 .
.
Formam minori de ordinul trei care il contin pe M.
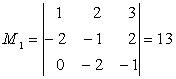 ;
; 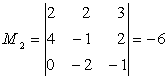 etc.
etc.
Cautam
minori de ordinul patru care incadreaza pe ![]()
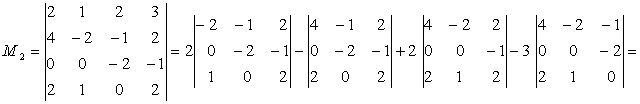
= ![]()
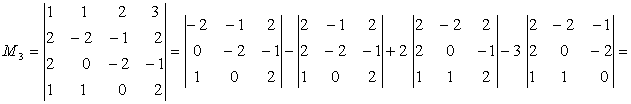
![]()
Cum ![]() este nenul
este nenul ![]()
EXERCITII DE REZOLVAT
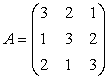 ;
; 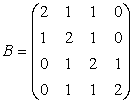 ;
; 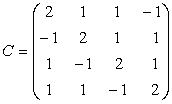


|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4131
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved