| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Despre o tehnica de inmultire rapida a numerelor intregi de mai multe cifre
Presupunem ca avem de
efectuat produsul a doua numere formate fiecare din doua cifre: ![]() si
si ![]() . Folosind scrierea in baza 10 a celor doua numere,
avem:
. Folosind scrierea in baza 10 a celor doua numere,
avem:
![]()
Daca facem inmultirea in scris, de exemplu pentru A=28 si B=73, avem:
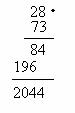
Tabelul urmator ilustreaza modul in care s-a calculat produsul anterior:
|
Puterile lui 10 | ||||
|
A | ||||
|
B | ||||
|
Inmultim toate cifrele lui A cu cifra unitatilor lui B | ||||
|
Inmultim toate cifrele lui A cu cifra zecilor lui B | ||||
|
Adunam pe coloane produsele intermediare de pe ultimele doua linii | ||||
|
Calculam rezultatul final, pastrand cifra unitatilor si "tinand minte" ceea ce ramane |
Observam ca pentru calcularea produsului a doua numere formate din cate 2 cifre este nevoie sa facem 4 inmultiri de numere de o cifra si 3 adunari.
Daca dorim in continuare sa
inmultim doua numere formate fiecare din cate 3 cifre: ![]() si
si ![]() , atunci folosind
descompunerea lor in baza 10 vom avea:
, atunci folosind
descompunerea lor in baza 10 vom avea:
![]()
si constatam din nou ca este nevoie de efectuarea a 9
inmultiri si a unui numar de adunari. In general, daca
trebuie sa facem produsul a doua numere de cate n cifre fiecare, este
nevoie de ![]() inmultiri si
un numar de adunari.
inmultiri si
un numar de adunari.
Vom aminti, in cele ce urmeaza, o alta modalitate de a inmulti 2 numere de cate n cifre fiecare. Ideea de baza este de a se micsora numarul de inmultiri, in scopul scaderii complexitatii operatiei.
Fie, in general, doua numere scrise in baza X (in prezent se foloseste baza 10, dar se pare ca in antichitate se foloseau si altele):
![]()
![]()
Produsul celor doua numere A (X) B (X) = P (X) este polinomul
![]()
Dar facand efectiv produsul celor doua numere obtinem:
![]() Egaland in
ultimele doua relatii coeficientii diferitelor puteri ale lui X,
obtinem :
Egaland in
ultimele doua relatii coeficientii diferitelor puteri ale lui X,
obtinem :
![]()
![]()
![]()
...........
![]()
Astfel, inmultirea a 2 numere mari A si B revine la a calcula termenii p0, ., p2n-2, la randul lor obtinuti prin produse de cifre si adunari.
In 1962, Karatsuba a
descoperit o metoda de a reduce numarul de calcule in cazul
inmultirii a doua numere. Pentru simplitate, vom considera produsul a
doua numere formate fiecare din cate 2 cifre: ![]() si
si ![]() . Produsul P (X) = A
(X) B (X) este:
. Produsul P (X) = A
(X) B (X) este:
![]()
unde:
![]()
![]()
![]()
Ideea lui Karatsuba a fost de a face notatiile:
![]()
![]()
![]()
din care rezulta:
![]()
![]()
![]()
Este evident ca pentru a face produsul a doua numere de cate doua cifre utilizam, in acest caz, 3 inmultiri : a0b0, a1b1 si (a0+a1) (b0+b1) in loc de 4, cate am fi facut la o inmultire obisnuita. Pretul platit pentru reducerea numarului de inmultiri il reprezinta aparitia operatiilor de scadere pe langa cele de adunare cu care eram obisnuiti.
Revenind la exemplul de inmultire de la inceput, pentru a face produsul 28 73 sunt necesare calculele: 2 10=100 si-n felul acesta:
![]()
rezultat gasit anterior prin inmultire obisnuita, facuta la scoala in clasele primare.
Sa extindem aceasta tehnica la efectuarea produsului a 2 numere A si B, fiecare de cate n cifre. Impartim numarul intreg A in doua bucati C si D, fiecare de cate n/2 cifre, iar numarul intreg B in doua bucati E si F, tot de cate n/2 cifre .Presupunem n ca fiind o putere a lui 2, caz in care impartirea in doua a numerelor se face fara probleme la fiecare pas, pana se ajunge la numere de o singura cifra, care se inmultesc direct. Atunci, se poate scrie:
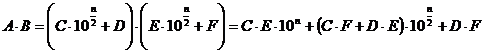
Pentru a calcula produsul A B avem nevoie de 4 produse partiale, de 3 adunari si de 2 inmultiri cu puteri ale lui 10.
Definind produsul:
![]()
putem scrie:
![]()
varianta in care folosim doar 3 inmultiri si chiar daca avem nevoie de un numar de 6 adunari si scaderi si 2 inmultiri cu puteri ale lui 10, complexitatea calculului se reduce.
Pentru n = 4, vom da un nou exemplu de aplicare a acestei tehnici: 1022
![]()
Procedeul continua pana cand se ajunge la inmultiri de dimensiuni elementare: n=1. Solutiile problemelor de dimensiuni elementare sunt combinate pentru a obtine solutiile subproblemelor de dimensiuni mai mari, inclusiv a problemei (de inmultire ) initiale. Aceasta metoda de a descompune o problema in mai multe subprobleme (de dimensiuni mai mici si implicit mai usor de solutionat) ce trebuie rezolvate la randul lor si de a gasi solutia problemei initiale combinand solutiile subproblemelor este numita "Divide et Impera" (dupa spusele lui Iulius Cezar, conform carora adversarii trebuie impartiti si divizati de luptele dintre ei, fiind astfel mult mai usor de controlat si invins).
Bibliografie:
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3057
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved