| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Diferentiabilitate in sens Gateaux
Ideea
fundamentala a calculului diferential este aproximarea locala a operatorilor
neliniari cu operatori liniari.Multa vreme aceasta idee n-a fost pusa in
evidenta datorita faptului ca in cazul dreptei reale (de fapt al oricarui
spatiu real unidimensional) exista o corespondenta biunivoca intre
functionalele liniare reale definite pe aceste spatii si numerele reale.Din
acest motiv derivata unei functii reale de o variabila reala(intr-un punct) se
defineste ca un numar.Data fiind ![]() si
si ![]() ,derivata
lui f in punctul
,derivata
lui f in punctul ![]() se defineste astfel:
se defineste astfel:
![]() (27)
(27)
In spiritul celor afirmate la inceput despre ideea fundamentala a calculului diferential,sa observam ca dreapta :
![]() (28)
(28)
reprezinta o aproximatie suficient de buna pentru f(x)
daca x este suficient de aproape de ![]() ,asa cum se
vede din formula :
,asa cum se
vede din formula :
![]() (29)
(29)
Fie ![]() si
si ![]() .Este
evident ca notiunea de derivata a lui f in
.Este
evident ca notiunea de derivata a lui f in ![]() introdusa cu (27) nu poate fi extinsa si la
acest caz,pentru simplul motiv ca operatia
introdusa cu (27) nu poate fi extinsa si la
acest caz,pentru simplul motiv ca operatia ![]() nu are de data aceasta sens (nu se poate aduna
un vector cu un scalar).Formula (27) sugereaza insa ideea de a defini
derivatele partiale ale lui f in punctul
nu are de data aceasta sens (nu se poate aduna
un vector cu un scalar).Formula (27) sugereaza insa ideea de a defini
derivatele partiale ale lui f in punctul ![]() ,dupa cum
urmeaza:
,dupa cum
urmeaza:
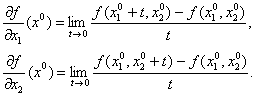
Sa revenim la
formula (27) .Fie ![]() Avem:
Avem:
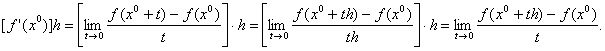
Interpretarea
![]()
are sens pentru f definita de la un spatiu vectorial X la un spatiu vectorial topologic Y,ceea ce conduce la urmatoarea definitie:
Definitie 8
Fie X un spatiu
vectorial, Y un spatiu vectorial topologic si ![]() .Fie
.Fie ![]() Se spune ca
operatorul P este diferentiabil in sens Gateaux in punctul x dupa directia h
daca exista urmatoarea limita:
Se spune ca
operatorul P este diferentiabil in sens Gateaux in punctul x dupa directia h
daca exista urmatoarea limita:
![]() (30)
(30)
Atunci ![]() se va numi diferentiala in sens Gateaux a
operatorului P in punctul x dupa directia h.
se va numi diferentiala in sens Gateaux a
operatorului P in punctul x dupa directia h.
Inspirati de
cazul ![]() ,vom folosi
in cele ce urmeaza notatia
,vom folosi
in cele ce urmeaza notatia ![]() in loc de
in loc de
![]() .Uneori vom folosi terminologia "G-diferentiabil" in loc de "diferentiabil in sens Gateaux".
.Uneori vom folosi terminologia "G-diferentiabil" in loc de "diferentiabil in sens Gateaux".
Exemplul 1:
Operatorul ![]() este G-diferentiabil in orice punct
este G-diferentiabil in orice punct ![]() dupa directia
dupa directia ![]() si
si ![]() Intr-adevar
,avem:
Intr-adevar
,avem:
![]()
Exemplul 2:
Fie ![]() ,baza canonica din
,baza canonica din ![]() si
si ![]() Daca exista
derivatele partiale ale lui f in punctul x ,
Daca exista
derivatele partiale ale lui f in punctul x ,![]() ,atunci f
este diferentiabila in sens Gateaux in punctul x dupa directiile
,atunci f
este diferentiabila in sens Gateaux in punctul x dupa directiile ![]() si
si
![]() .
.
Intr-adevar,avem:
![]()
Exemplul 3:
Fie ![]() dupa cum urmeaza:
dupa cum urmeaza:

Este usor de vazut ca derivatele partiale ale lui f in
punctul 0 exista si ![]() .
.
Conform rezultatului stabilit la exemplul 2 exista ![]() si avem :
si avem :
![]()
Fie un vector oarecare ![]() din
din ![]() .Exista
.Exista ![]() Pentru
aceasta trebuie sa existe limita:
Pentru
aceasta trebuie sa existe limita:
![]() (31)
(31)
Se vede ca aceasta limita exista daca si numai daca h are una dintre formele:
![]()
si ca atunci:
![]() (32)
(32)
Exemplul 3 arata ca pentru o functie ![]() existenta derivatelor partiale in punctul x nu
este o conditie suficenta pentru ca f sa fie G-diferentiabila in punctul x dupa
orice directie h.
existenta derivatelor partiale in punctul x nu
este o conditie suficenta pentru ca f sa fie G-diferentiabila in punctul x dupa
orice directie h.
Propozitie 3:
Fie X un spatiu vectorial,Y un spatiu vectorial topologic,![]() si
si ![]() Daca P este
G-diferentiabil in x dupa directia h,atunci P este G-diferentiabil in x dupa
directia
Daca P este
G-diferentiabil in x dupa directia h,atunci P este G-diferentiabil in x dupa
directia ![]() si :
si :
![]() . (33)
. (33)
Demonstratie:
Daca ![]() sau
sau ![]() ,propozitia
este adevarata in virtutea exemplului 1.Putem presupune deci ca
,propozitia
este adevarata in virtutea exemplului 1.Putem presupune deci ca ![]() .Avem
(utilizand faptul ca intr-un spatiu vectorial topologic inmultirea cu scalari
este o operatie continua):
.Avem
(utilizand faptul ca intr-un spatiu vectorial topologic inmultirea cu scalari
este o operatie continua):
![]() Definitie 9:
Definitie 9:
Se spune ca operatorul ![]() este G-diferentiabil in punctul
este G-diferentiabil in punctul ![]() daca este G-diferentiabil in x dupa orice
directie
daca este G-diferentiabil in x dupa orice
directie ![]() Operatorul
Operatorul ![]() este G-diferentiabil pe X daca este
G-diferentiabil in orice punct
este G-diferentiabil pe X daca este
G-diferentiabil in orice punct ![]() .
.
Fie ![]() G-diferentiabil in punctul
G-diferentiabil in punctul ![]() si fie
si fie ![]() dupa cum urmeaza:
dupa cum urmeaza:
![]()
Operatorul ![]() se va numi diferentiala in sens Gateaux
(G-diferentiabila) operatorului P in punctul x.Din propozitia 3 rezulta ca
G-diferentiala lui P in punctul x este un operator omogen definit de la X la
Y.In baza acestor observatii punem urmatoarea definitie:
se va numi diferentiala in sens Gateaux
(G-diferentiabila) operatorului P in punctul x.Din propozitia 3 rezulta ca
G-diferentiala lui P in punctul x este un operator omogen definit de la X la
Y.In baza acestor observatii punem urmatoarea definitie:
Definitie 10:
Fie ![]() si
si ![]() multimea operatorilor omogeni definiti de la X
la Y.Spunem ca P este G-diferentiabil pe X daca exista un operator
multimea operatorilor omogeni definiti de la X
la Y.Spunem ca P este G-diferentiabil pe X daca exista un operator ![]() astfel incat:
astfel incat:
![]() (34)
(34)
Notiunea de
diferentiabilitate in sens Gateaux poate fi introdusa intr-un cadru mai
general,anume pentru aplicatii ![]() ,X si Y
fiind doua spatii vectoriale cu convergenta.Pentru scopul pe care il urmarim in
lucrarea noastra ,cadrul spatiilor normate,reale este suficient.De aceea vom
reformula definitia si vom obtine,in continuare cateva rezultate specifice.Inainte
de a face acest lucru sa remarcam urmatoarele : in definitia diferentiabilitatii dupa Gateaux se pretinde
ca numai in spatiul Y(spatiul in care P ia valori ) sa avem definita o
topologie.Pe de alta parte,daca se introduce functia de variabila scalara
,X si Y
fiind doua spatii vectoriale cu convergenta.Pentru scopul pe care il urmarim in
lucrarea noastra ,cadrul spatiilor normate,reale este suficient.De aceea vom
reformula definitia si vom obtine,in continuare cateva rezultate specifice.Inainte
de a face acest lucru sa remarcam urmatoarele : in definitia diferentiabilitatii dupa Gateaux se pretinde
ca numai in spatiul Y(spatiul in care P ia valori ) sa avem definita o
topologie.Pe de alta parte,daca se introduce functia de variabila scalara
![]() ,
,
avem:
![]() .
.
Aceasta a facut ca mult timp in analiza proprietatilor aplicatiilor G-diferentiabile sa se utilizeze numai proprietatile topologice ale dreptei reale R sau ale lui C.O serie de notiuni fundamentale,cum ar fi cea de convergenta,de exemplu,nu puteau fi insa discutate de o maniera convenabila.Aceasta a impus introducerea unei topologii si pe X.In cazul in care aceasta topologie este generata de o norma,chiar daca avem o micsorare a generalitatii,beneficiem de posibilitatea utilizarii puternicelor instrumente analitice de care dispune analiza functionala.
Fie asadar,X si Y doua spatii normate reale.Utilizam urmatoarele notatii:
![]() -multimea
operatorilor omogeni definiti de la X in
-multimea
operatorilor omogeni definiti de la X in
![]()
L(X,Y)-multimea operatorilor liniari definiti de la X in
![]()
. L(X,Y)- multimea operatorilor liniari si
marginiti definiti de la X in ![]()
Definitie 11
Fie X si Y doua
spatii normate reale si ![]() un operator (liniar sau neliniar).
un operator (liniar sau neliniar).
a) Operatorul P se numeste diferentiabil in sens Gateaux pe X(G-diferentiabil pe X) daca exista un operator (VP),
![]() (35)
(35)
astfel incat:
![]() (36)
(36)
b) Daca exista un operator (DP),
![]() (37)
(37)
astfel incat:
![]() (38)
(38)
se spune ca P este G-diferentiabil cu diferentiabila in sens Gateaux liniara pe X.
c) In sfarsit,daca exista P',
![]() L (X,Y) (39)
L (X,Y) (39)
astfel incat:
![]() (40)
(40)
se spune ca P este derivabil in sens Gateaux pe X.
Evident,egalitatea (36) trebuie inteleasa astfel:
![]()
Semnificatii analoage pentru (38) si (40).
Daca in definitia
11 x apartine unei multimi ![]() , h
ramanand arbitrar in X,se spune ca P este G-diferentiabil (respectiv
G-diferentiabil cu diferentiala liniara,respectiv G-derivabil ) pe
, h
ramanand arbitrar in X,se spune ca P este G-diferentiabil (respectiv
G-diferentiabil cu diferentiala liniara,respectiv G-derivabil ) pe ![]() .Mai
precis,avem urmatoarea definitie:
.Mai
precis,avem urmatoarea definitie:
Definitie 12
Fie X si Y doua
spatii normate reale si ![]() .Operatorul
P se numeste G-diferentiabil pe multimea
.Operatorul
P se numeste G-diferentiabil pe multimea ![]() daca exista un operator (VP),
daca exista un operator (VP),
![]() (41)
(41)
astfel incat:
![]() (42)
(42)
Daca exista (DP),
![]() (43)
(43)
astfel incat:
![]() (44)
(44)
se spune ca P
este G-diferentiabil pe ![]() ,cu
diferentiala in sens Gateaux liniara.
,cu
diferentiala in sens Gateaux liniara.
In sfarsit,daca exista:
![]() L
L![]()
astfel incat:
![]() (46)
(46)
se spune ca P
este derivabil in sens Gateaux pe ![]() . (47)
. (47)
Observatii
1.Daca ![]() este deschisa,definitia 12 are sens chiar daca
P nu este definit pe tot spatiul ci doar pe
este deschisa,definitia 12 are sens chiar daca
P nu este definit pe tot spatiul ci doar pe ![]() .Fie,intr-adevar,
.Fie,intr-adevar,![]() .Exista o
sfera deschisa
.Exista o
sfera deschisa ![]() astfel incat
astfel incat 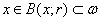 .Fie h
arbitrar in X,
.Fie h
arbitrar in X,![]() .Pentru
orice t cu
.Pentru
orice t cu ![]() ,punctul
,punctul ![]() ,deci are
sens
,deci are
sens ![]() si pentru a recalcula diferentiala in sens
Gateaux a lui P in punctul x dupa directia h este suficient sa consideram:
si pentru a recalcula diferentiala in sens
Gateaux a lui P in punctul x dupa directia h este suficient sa consideram:
![]()
2.Daca in
definitia 12 ![]() se reduce la un punct,se obtine definitia
diferentiabililtatii operatorului P intr-un punct.
se reduce la un punct,se obtine definitia
diferentiabililtatii operatorului P intr-un punct.
3.Daca ![]() este liniar,atunci P este diferentiabil(cu
diferentiala in sens Gateaux liniara pe X) si:
este liniar,atunci P este diferentiabil(cu
diferentiala in sens Gateaux liniara pe X) si:
![]()
Intr-adevar,tinand seama de liniarittatea lui P,avem:
![]()
Evident,daca ![]() este liniar si marginit,atunci P este
derivabil in sens Gateaux pe X si
este liniar si marginit,atunci P este
derivabil in sens Gateaux pe X si ![]() Aceasta
ultima observatie arata ca diferentiabilitatea in sens Gateaux este o notiune
interesanta numai pentru operatorii neliniari.
Aceasta
ultima observatie arata ca diferentiabilitatea in sens Gateaux este o notiune
interesanta numai pentru operatorii neliniari.
4.Observam ca daca in definitia 11 Y este dreapta reala cu norma data de modul,atunci se obtine definitia corespunzatoare pentru diferentiabilitatea in sens Gateaux a functionalelor neliniare pe spatii normate reale.In particular,definitia ce se obtine particularizand punctul c) al definitiei 11 va juca un rol important in cele ce urmeaza:
Definitie 13
Fie X un spatiu
normat real,![]() .Functionala
f se numeste derivabila in sens Gateaux pe X daca exista operatorul
.Functionala
f se numeste derivabila in sens Gateaux pe X daca exista operatorul
![]() L
L![]()
![]()
astfel incat:
![]() (48)
(48)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2550
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved