| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Putem vorbi de existenta unui cuplu, primal-dual, de probleme de programare liniara care se pot utiliza in modelarea matematica a fenomenelor economice.
Fie modelele de programare liniara (P.L.):
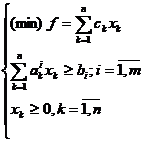 (1)
(1) 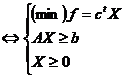
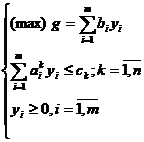 (2)
(2) 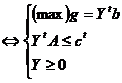
Definitie:
Modelele (1) si (2) sunt modele de programare liniara (P.L.) aflate in relatia de dualitate simetrica (modelul (1) este dualul modelului (2) si invers).
Exemplu:
Fie problema de P.L.:
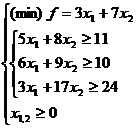
Pentru modelul dual, avem urmatoarele elemente constitutive:
In final, modelul dual va fi:
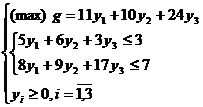
Corespondenta biunivoca a cuplurilor de probleme este pusa in evidenta de teoremele dualitatii prezentate si demonstrate mai jos:
Teorema:
Fie X0 o solutie admisibila pentru modelul (1), cu valoarea functiei obiectiv f0=f(X0); fie Y0 o solutie admisibila pentru modelul (2), cu valoarea functiei obiectiv g0=g0(Y0);
Atunci avem f0 g0.
Demonstratie:
Avem evident f(X0)=ctX0, g0(Y0)=Y0tb;
din AX0 -b 0 si din Y0t 0 TY0t(AX0-b) 0
din ct-Y0tA 0 si din X0 0 T (ct-Y0tA)X0 0
Adunand relatiile de mai sus obtinem:
(ct-Y0tA)X0+Y0t(AX0-b) 0 ctX0-Y0tb 0 deci f0-g0 0
Teorema
Fie X0 o solutie admisibila (program) pentru modelul (1) si Y0 o solutie admisibila (program) pentru modelul (2); daca avem relatia f(X0)=g(Y0), atunci:
- X0 este o solutie optima (program optim) pentru modelul (1)
- Y0 este o solutie optima (program optim) pentru modelul (2)
Demonstratie:
Presupunem ca X0 nu ar fi solutie optima pentru modelul(1), deci ar exista o solutie admisibila pentru (1) notata cu X1, pentru care f(X0)>f(X1) ctX0>ctX1.
Dar ctX0 = Y0tb, ctX1 < ctX0 T ctX1 <Y0tb, ceea ce nu este posibil, conform teoremei 1.
Presupunem ca y0 nu ar fi solutie optima pentru modelul (2) deci ar exista o solutie admisibila pentru (2) notata cu Y1, pentru care g(Y0) < g(Y1) Y0tb < Y1tb
Dar ctX0 = Y0tb, Y1tb < Y1tb ctX0 < Y1tb, ceea ce nu este posibil conform teoremei 1.
Teorema:
Daca una dintre problemele (1), (2) are functia obiectiv nemarginita, atunci cealalta problema nu are solutii admisibile.
Demonstratie:
Presupunem ca modelul (2) ar avea solutia admisibila Y0. Cum functia f(X) = ctX este nemarginita inferior, deducem ca exista o solutie admisibila X1, pentru care ctX1 < Y0tb, aceea ce este absurd conform teoremei 1.
Exista insa modele care nu au forma ceruta de catre dualitatea simetrica, adica:
- nu toate restrictiile au inegalitati pentru problema de maxim
- nu toate restrictiile au inegalitati pentru problema de minim
- nu toate variabilele modelului dat sunt nenegative ( 0).
Totusi, s-a pus la punct o modalitate de a constitui dualul oricarui model. Principalele teoreme corespunzatoale acestui tip de dualitate, numita dualitate nesimetrica, nu vor fi enuntate; afirmam numai ca sunt valabile aceleasi teoreme ca si in cazul dualitatii simetrice.
Ansamblul regulilor de scriere a unui astfel de model de dualitate nesimetrica sunt prezentate in continuare:
categorii de variabile
variabile nenegative: xj 0
variabile nepozitive: xj 0
variabile libere: xjIR
categorii de restrictii:
restrictii concordante:
pentru minim : cu
pentru maxim : cu
restrictii necorcondante:
pentru minim : cu
pentru maxim : cu
restrictii egalitati
reguli de corespondenta:
|
modelul primal |
modelul dual |
|
variabila nenegativa |
restrictie concordanta |
|
restrictie concordanta |
variabila nenegativa |
|
variabila nepozitiva |
restrictie neconcordanta |
|
restrictie neconcordanta |
variabila nepozitiva |
|
variabila libera |
restrictie egalitate |
|
restrictie egalitate |
variabila libera |
|
maxim |
minim |
|
minim |
maxim |
|
variabila structurala |
variabila de compensare |
|
variabila de compensare |
variabila structurala |
|
variabila(vector)aflata in baza |
variabila (vector) din afara bazei |
|
variabila (vector) din afara bazei |
variabila (vector) aflata in baza |
|
coloana b dintr-un tabel simplex |
liniaDkdin tabelul simplex (eventual cu schimbare de semn) |
|
liniaDkdin tabelul simplex (eventual cu schimbare de semn) |
coloana b dintr-un tabel simplex |
De exemplu:
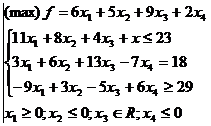
Modelul dat nu se incadreaza in dualitatea simetrica si constatam urmatoarele:
modelul dual:
va fi de minim;
va avea 4 restrictii;
va avea 3 variabile, anume y1, y2, y3
in modelul primal:
prima restrictie este concordanta, deci y1 0;
a dou restrictie este egalitate, deci y2IR;
a treia restrictie este neconcordanta, deci y3 0.
in modelul primal:
x1 este nenegativa, deci prima restrictie duala va fi concordanta (deci
x2 este nepozitiva, deci a doua restrictie duala va fi necorcondanta (deci
x3 este libera, deci a treia restrictie duala va fi egalitate;
x4 este nepozitiva, deci a patra restrictie duala va fi necorcondanta (deci
Modelul dual va fi deci:
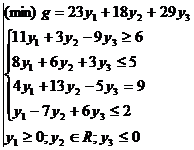
Rezolvam urmatoarea problema economica pentru a vedea semnificatia economica a variabilelor duale si a interpreta rezultatele dualei pe tabelul simplex
Consideram o unitate economica care fabrica
produsele ![]() si
si ![]() . Pentru obtinerea lor se utilizeaza trei
resurse: forta de munca, mijloace de munca si materii
prime. In tabelul urmator se dau consumurile specifice si cantitatile
disponibile din cele trei resurse, precum si preturile de vanzare ale
produselor.
. Pentru obtinerea lor se utilizeaza trei
resurse: forta de munca, mijloace de munca si materii
prime. In tabelul urmator se dau consumurile specifice si cantitatile
disponibile din cele trei resurse, precum si preturile de vanzare ale
produselor.
|
Resurseproduse |
P1 |
P2 |
P3 |
Disponibil (unitati fizice) |
|
Forta de munca |
1 |
3 |
4 |
15 |
|
Mijloace de munca |
2 |
5 |
1 |
10 |
|
Materii prime |
4 |
1 |
2 |
25 |
|
Pret de vanzare (unitati monetare) |
3 |
2 |
6 |
|
Modelul matematic pe baza caruia se stabileste programul optim de productie, avand drept criteriu de eficienta valoarea maxima a productiei, are forma:
max![]()
in conditiile:
![]()
![]()
![]()
![]()
![]() (j=1,2,3)
(j=1,2,3)
Utilizand regulile de dualitate prezentate mai inainte rezulta urmatoarea problema duala de programare liniara:
min![]()
in conditiile:
![]()
![]()
![]()
![]()
![]() (j=1,2,3)
(j=1,2,3)
Solutia optima a
problemei primale este prezentata in tabelul simplex final, unde ![]() se testeaza la
criteriul de optim daca sunt
se testeaza la
criteriul de optim daca sunt ![]()
|
|
|
|
3 |
2 |
6 |
0 |
0 |
0 |
cj |
|
CB |
B |
XB |
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
|
|
0 |
a4 |
15 |
1 |
3 |
4 |
1 |
0 |
0 |
3/4 |
|
0 |
a5 |
10 |
2 |
5 |
1 |
0 |
1 |
0 |
2/1 |
|
0 |
a6 |
25 |
4 |
1 |
2 |
0 |
0 |
1 |
6/2 |
|
|
zj |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
-3 |
-2 |
-6 |
0 |
0 |
0 |
|
|
6 |
a3 |
15/4 |
1/4 |
3/4 |
1 |
1/4 |
0 |
0 |
3 |
|
0 |
a5 |
25/4 |
7/4 |
17/4 |
0 |
-1/4 |
1 |
0 |
5/7 |
|
0 |
a6 |
70/4 |
14/4 |
-2/4 |
0 |
-2/4 |
0 |
1 |
9/7 |
|
|
zj |
90/2 |
3/2 |
9/2 |
6 |
3/2 |
0 |
0 |
|
|
|
|
|
-3/2 |
5/2 |
0 |
3/2 |
0 |
0 |
|
|
6 |
a3 |
20/7 |
0 |
1/7 |
1 |
2/7 |
-1/7 |
0 |
|
|
3 |
a1 |
25/7 |
1 |
17/7 |
0 |
-1/7 |
4/7 |
0 |
|
|
0 |
a6 |
35/7 |
0 |
-9 |
0 |
0 |
-2 |
1 |
|
|
|
zj |
195/7 |
3 |
57/7 |
6 |
9/7 |
6/7 |
0 |
|
|
|
|
|
0 |
43/7 |
0 |
9/7 |
6/7 |
0 |
|
Dupa cum s-a aratat, prin rezolvarea uneia dintre problemele cuplului primala-duala se obtin solutiile ambelor probleme.
In cazul examinat, solutia optima a problemei duale se citeste pe linia z la intersectia cu coloanele vectorilor a4 a5 , si a6 care au format baza initiala, deci:
![]() si
si ![]()
Este usor de verificat ca ![]() Spre exemplu
Spre exemplu ![]() rezulta din relatia:
rezulta din relatia:
![]()
Pe baza rezultatelor obtinute se verifica imediat ca
max[Z(x)]=min[G(u)]:
max[Z(x)]=![]() unitati monetare
unitati monetare
min[G(u)]=![]() unitati monetare.
unitati monetare.
Concluzii: Fie cuplul de probleme duale:
|
max [Z(x)]=
|
min [G(
|
i) Tabelul simplex final corespunzator problemei primale contine atat solutia optima a problemei primale cat si a problemei duale.
ii)
Solutia problemei primale ![]() se obtine pe coloana
vectorului b, iar solutia problemei duale
se obtine pe coloana
vectorului b, iar solutia problemei duale ![]() se obtine pe
linia z la intersectia cu coloanele vectorilor care au format baza
initiala.
se obtine pe
linia z la intersectia cu coloanele vectorilor care au format baza
initiala.
Teorema ecarturilor complementare:
O conditie necesara
si suficienta pentru ca un cuplu de solutii admisibile de
baza ![]() si
si ![]() sa fie optim, este ca solutiile sa
verifice simultan relatiile:
sa fie optim, este ca solutiile sa
verifice simultan relatiile:
![]()
![]()
Pe baza acestor relatii se pot formula urmatoarele concluzii:
a)daca
![]() atunci
atunci ![]()
b)daca
![]() atunci
atunci ![]()
c)daca
![]() atunci
atunci ![]() ;
;
d)daca
![]() atunci
atunci ![]()
Prima relatie arata
ca variabila duala corespunzatoare unei resurse utilizata
in intregime are o valoare pozitiva, iar cea de a doua arata ca ![]() daca resursa i nu este utilizata in
intregime.
daca resursa i nu este utilizata in
intregime.
Analizand
punctele c si d se trage concluzia ca, daca costul unitar al
activitatii ![]() ,obtinut prin evaluarea consumurilor specifice
,obtinut prin evaluarea consumurilor specifice ![]() cu ajutorul
componentelor solutiei optime a problemei duale, este egal cu coeficientul
cu ajutorul
componentelor solutiei optime a problemei duale, este egal cu coeficientul
![]() din functia
obiectiv (de exemplu beneficiul unitar) atunci componenta
din functia
obiectiv (de exemplu beneficiul unitar) atunci componenta ![]() iar daca acest cost este mai mare decat
iar daca acest cost este mai mare decat ![]() , atunci nu este eficient sa includem in programul optim
activitatea j (ca urmare
, atunci nu este eficient sa includem in programul optim
activitatea j (ca urmare ![]() ).
).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 940
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved