| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Diferentiabilitate in sens Frechet
Fie X si Y doua spatii normate reale.
Definitia 16
Un operator ![]() se numeste diferentiabil in sens Frechet in
punctul
se numeste diferentiabil in sens Frechet in
punctul ![]() daca exista un operator
daca exista un operator ![]() L(X,Y) astfel incat:
L(X,Y) astfel incat:
![]() (148)
(148)
cu :
![]() (149)
(149)
Operatorul P se numeste diferentiabil in sens Frechet pe X daca este diferentiabil in orice punct din X,ceea ce,tinand seama de definitia 16,permite sa punem urmatoarea definitie:
Definitia 17
Operatorul ![]() se numeste diferentiabil in sens Frechet pe X
daca exista un operator:
se numeste diferentiabil in sens Frechet pe X
daca exista un operator:
![]() L(X,Y) (150)
L(X,Y) (150)
astfel incat
pentru orice ![]()
![]() ,
,
![]()
Se observa
imediat din (148) ca ![]() La fel,este
evident ca (148) si (149) pot fi scrise sub forma echivalenta:
La fel,este
evident ca (148) si (149) pot fi scrise sub forma echivalenta:
![]() (151)
(151)
Observatii
1.In timp ce
diferentiala in sens Gateaux a operatorului P in punctul x,(VP)(x) era un
element din ![]() ,diferentiala
in sens Frechet a operatorului P in punctul x este ,prin definitie,un element
din L(X,Y).
,diferentiala
in sens Frechet a operatorului P in punctul x este ,prin definitie,un element
din L(X,Y).
2.Din (151)
rezulta ca daca P este Frechet-diferentiabil in ![]() ,atunci
pentru orice
,atunci
pentru orice ![]() exista
exista ![]() astfel incat pentru orice h cu
astfel incat pentru orice h cu ![]() avem:
avem:
![]() (152)
(152)
Din aceasta ultima inegalitate rezulta imediat:
![]()
care permite sa enuntam urmatoarea:
Propozitie 5
Daca ![]() este Frechet-diferentiabil in punctul
este Frechet-diferentiabil in punctul ![]() ,atunci P
este continuu in x.
,atunci P
este continuu in x.
Diferentiabilitatea in sens Frechet raspunde astfel unei exigente pe care suntem tentati s-o impunem oricarui tip de diferentiabilitate:aceea ca aplicatiile diferentiabile sa fie continue.Din acest punct de vedere,diferentiabilitatea in sens Gateaux ofera mult mai putin:din existenta diferentialei in sens Gateaux intr-un punct nu rezulta in mod necesar continuitatea aplicatiei in acel punct.
Iata un exemplu
foarte simplu in acest sens:aplicatia ![]() dupa cum urmeaza:
dupa cum urmeaza:
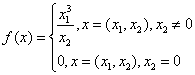
este derivabila
in sens Gateaux in punctul ![]() si
si ![]() dar aplicatia
dar aplicatia ![]() nu este continua in
nu este continua in ![]() .
.
Propozitie 6
Daca ![]() este G-diferentiabil in punctul
este G-diferentiabil in punctul ![]() ,atunci P
este continuu in x dupa orice directie,adica:
,atunci P
este continuu in x dupa orice directie,adica:
![]() (153)
(153)
Demonstratie
Intr-adevar,din faptul ca:
![]()
rezulta:
![]() (154)
(154)
cu ![]() cand
cand ![]() (este suficient pentru aceasta sa se ia
(este suficient pentru aceasta sa se ia ![]() ).Din (154)
rezulta:
).Din (154)
rezulta:
![]()
din care,trecand
la limita cu ![]() ,rezulta
(153).
,rezulta
(153).
Observatie
Inlocuind in (148) h cu th ,rezulta:
![]() ,
,
ceea ce demonstreaza:
Propozitia 7
Daca P este
Frechet-diferentiabil in punctul x,atunci este G-derivabil si ![]()
Observatie
Propozitia 7 demonstreaza si unicitatea diferentialei Frechet intr-un punct,in ipoteza ca aceasta exista.Reciproca propozitiei 7 nu este,in general,adevarata.
Teorema 23
Fie X si Y doua
spatii normate reale si ![]() .
.
Presupunem ca:
P
este derivabil in sens Gateaux in orice punct al multimii ![]() ,U fiind o vecinatate a punctului
,U fiind o vecinatate a punctului ![]() ;
;
operatorul
P' este continuu in ![]() in raport cu multimea
in raport cu multimea ![]()
Atunci P este
Frechet-diferentiabil in ![]() si
si ![]() .
.
Demonstratie
Fie ![]() astfel incat
astfel incat ![]() .Vom arata
ca ,in conditiile teoremei,
.Vom arata
ca ,in conditiile teoremei,![]() poate juca
rolul lui
poate juca
rolul lui ![]() ,cu alte
cuvinte exista
,cu alte
cuvinte exista ![]() astfel incat:
astfel incat:
![]() (155)
(155)
si
![]() (156)
(156)
Pentru a satisface (155) este suficient sa alegem:
![]()
iar pentru a
incheia demonstratia mai trebuie aratat ca ![]() astfel ales satisface (156).
astfel ales satisface (156).
Fie ![]() astfel incat
astfel incat ![]()
Avem:
![]()
![]()
![]()
![]()
de unde:
![]()
din care,trecand
cu limita cu ![]() si utilizand continuitatea lui P' in punctul
si utilizand continuitatea lui P' in punctul ![]() ,rezulta:
,rezulta:![]() Teorema e
demonstrata.
Teorema e
demonstrata.
Exemplul 10
Fie ![]() .Presupunem
ca
.Presupunem
ca ![]() este diferentiabila in sens Frechet in punctul
este diferentiabila in sens Frechet in punctul
![]() Sa calculam
Sa calculam
![]() .Avem:
.Avem:
![]()
unde ![]() .
.
Fie ![]() ,unde cu
,unde cu ![]() a fost notata baza canonica in
a fost notata baza canonica in ![]() Avem:
Avem:
![]() ,
,
deci pentru a
calcula ![]() este suficient sa calculam
este suficient sa calculam ![]() .Dar
conform propozitiei 7 avem:
.Dar
conform propozitiei 7 avem:
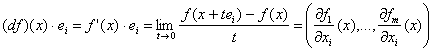
astfel incat:
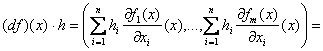
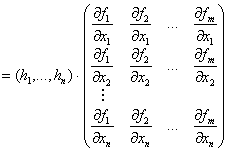
Exemplul 11
Fie ![]() spatiul functiilor (reale) continue pe
spatiul functiilor (reale) continue pe ![]() ,normat cu
norma:
,normat cu
norma:![]()
Fie ![]() astfel:
astfel:
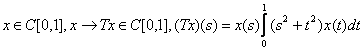 .
.
Este usor de
aratat ca T este diferentiabil in sens Gateaux in orice punct ![]() si ca
si ca ![]() este definita astfel:
este definita astfel:
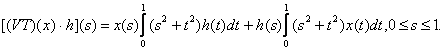
Pe aceasta
formula se vede clar ca diferentiala lui
T in x este liniara in h.Se arata usor ca G-diferentiala lui T in x,ca operator
de la ![]() la
la ![]() ,este un
operator marginit.
,este un
operator marginit.
Intr-adevar,
![]() =
=
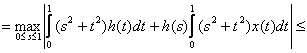
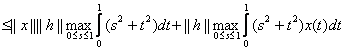 .
.
In consecinta,T
este G-derivabil pe ![]() .Pe de alta
parte,daca notam:
.Pe de alta
parte,daca notam:
![]() ,
,
Se vede imediat
ca ![]() ,unde
,unde 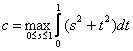 .De aici
rezulta ca
.De aici
rezulta ca![]() deci T este
Frechet-diferentiabil pe
deci T este
Frechet-diferentiabil pe ![]() iar
iar ![]() este elementul din
este elementul din ![]() definit astfel:
definit astfel:
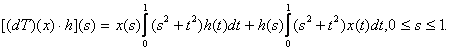
Exemplul 12
Fie ![]() functie continua si fie
functie continua si fie ![]() urmatoarea functionala pe
urmatoarea functionala pe ![]() :
:
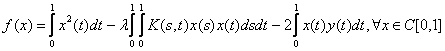 ,
,
y fiind un
element fixat in ![]() .Functionala
.Functionala
![]() este G-derivabila pe
este G-derivabila pe ![]() si
si ![]() ,
,
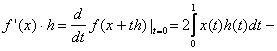
-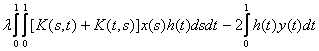 .
.
Se arata de asemenea ca daca punem:
![]() ,
,
atunci ![]() deci
deci ![]() este Frechet-diferentiabila pe
este Frechet-diferentiabila pe ![]() .
.
Observatie
Fie X si Y spatii
normate reale si ![]() .Daca P
este Frechet-diferentiabil in
.Daca P
este Frechet-diferentiabil in ![]() ,atunci din
(152) urmeaza ca daca x este suficient de "aproape" de
,atunci din
(152) urmeaza ca daca x este suficient de "aproape" de ![]() ,atunci:
,atunci:
![]() este suficient de
aproape de zero;cu alte cuvinte,
este suficient de
aproape de zero;cu alte cuvinte,
![]() (157)
(157)
Daca ![]() atunci in (157) se recunoaste aproximarea
valorii in P in punctul x cu valoarea pe care o ia in x tangenta la graficul
lui P in
atunci in (157) se recunoaste aproximarea
valorii in P in punctul x cu valoarea pe care o ia in x tangenta la graficul
lui P in ![]() Daca
Daca ![]() ,atunci
(157) devine:
,atunci
(157) devine:
![]()
pe care se
recunoaste aproximarea valorii pe care o ia P in punctul ![]() cu valoarea pe care planul tangent in
cu valoarea pe care planul tangent in ![]() o ia in
o ia in ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2485
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved