| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
a) Modul de determinare a punctelor de extrem pentru functii:
de o variabila,
multivariabile.
Se vor prezenta metoda perturbatiilor (sau a variatiilor) a lui Lagrange si metoda calculului variational in vederea investigarii unui punct de minim, apoi vor fi deduse conditiile suficiente de optim in termenii ecuatiei Hamilton-Jacobi.
Extremele unei functii= determinarea punctelor de minim si/sau de maxim.
Observatie:
Problemele puse in acest subcapitol sunt legate de:
1) existenta unui minim,
2) de unicitatea acestuia,
3) de posibilitatea investigarii unui minim.
 Extremele
functiilor de o variabila reala
Extremele
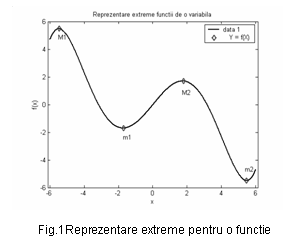
functiilor de o variabila reala Fie o functie reala definta pe multimea valorilor reale (fig.1). Din reprezentarea grafica 1 se observa ca:
odata cu cresterea abscisei pe intervalul (- ,M1), valorile ordonatelor cresc,
in intervalul (M1,m1) ordonatele descresc
in intervalul (m1,M2), ordonatele cresc monoton.
Punctul xM1 este un maxim local deoarece intr-o vecinatate convenabil aleasa x, valorile functiei f(x), pentru oricare x diferit de xM1, sunt mult mai mici decat f(xM1).
Similar xm1 minim local.
[Transpunerea matematica a celor doua concluzii se realizeaza dupa cum urmeaza.]
Un punct x* din A se numeste minim local al functiei f daca exista un e>0, suficient de mic, astfel incat pentru oricare x aflat intr-o vecinatate a lui x*, adica:
![]() (1)
(1)
f(x*) nu depaseste valoarea lui f(x):
![]() (2)
(2)
Un punct x* din A se numeste minim global (absolut) al functiei f daca
![]() (3)
(3)
pentru toti x din A
Un punct x* din A se numeste maxim local a functiei f daca exista un e>0, suficient de mic, astfel incat pentru oricare x aflat intr-o vecinatate a lui x*, adica:
![]() (4)
(4)
f(x) nu depaseste valoarea lui f(x*):
![]() (5)
(5)
Un punct x* din A se numeste maxim global (absolut) al functiei f daca
![]() (6)
(6)
pentru toti x din A
Se stie ca derivata unei functii continue la trecerea printr-un punct de extrem isi schimba semnul (fig.3). Astfel, pentru punctul de maxim M1, functia f(x) este crescatoare pentru x<xM1, derivata de ordinul I fiind pozitiva la stanga punctului de maxim:
![]() (7)
(7)
si f(x) descrescatoare pentru x>xM1, derivata devenind negativa la dreapta acestui punct:
![]() (8)
(8)
Analog, pentru un punct de minim, m1, functia f(x)este descrescatoare pentru x<xm1, derivata de ordinul I fiind negativa la stanga punctului de minim:
![]() , (9)
, (9)
si crescatoare pentru x>xm1, derivata fiind pozitiva la dreapta acestui punct:
![]() (10)
(10)
Concluzie: derivata de ordinul I trebuie sa se anuleze la trecerea prin punctele de maxim local sau de minim local (fig.1):
![]() (11)
(11)
Relatia (11), care nu este decat conditia de anulare a derivatei de ordinul I, reprezinta conditia necesara de existenta a unui punct de extrem.
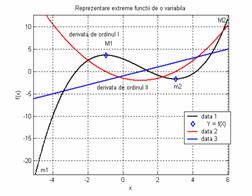
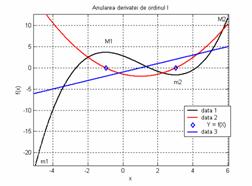
Fig.2 Reprezentare extreme pentru o functie reala. Fig.3 Anularea derivatei de ordinul I
Variatia derivatei de ordinul I (fig.3) a unei functii de o variabila reala (fig.2) se studiaza cu ajutorul derivatei de ordinul II. Daca derivata de ordinul II este negativa la trecerea functiei printr-un punct de extrem, atunci punctul de extrem (xM1) este un maxim (fig.4).
![]() (12)
(12)
Daca derivata de ordinul II este pozitiva la trecerea functiei printr-un punct de extrem, atunci punctul de extrem (xm2) este un minim (fig.4).
![]() (13)
(13)
Relatiile (12), (13) separa punctele de extrem in maxime si minime si reprezinta conditiile suficiente, garantand existenta unui maxim sau minim atunci cand sunt indeplinite.
Concluzie:
pentru cazul in care derivata de ordinul I exista in toate punctele domeniului A
- punctul xm2 este un minim local al functiei f(x), daca sunt indeplinite conditiile de necesitate (9) si suficienta (13
- punctul xm2 este un minim global, daca pentru oricare alt x, xm2 este cel mai mic minim local:
![]() .(14)
.(14)
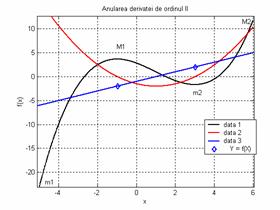
Fig.4 Anularea derivatei de ordinul II.
Fie o functie f(x) definita pe un interval inchis ![]() ,
continua si derivabila. [Prin urmare, exista valori x pentru care functia f(x) are extreme (fig. 5)].
,
continua si derivabila. [Prin urmare, exista valori x pentru care functia f(x) are extreme (fig. 5)].
Astfel, pentru punctul a, functia este crescatoare pentru x>xa, derivata de ordinul I fiind pozitiva la dreapta punctului a:
![]() ,(15)
,(15)
valoarea functiei in punctul a, f(a), conform (10) este un punct de minim local.
Pentru punctul b, functia este descrescatoare pentru x<xb, derivata de ordinul I fiind negativa la stanga punctului b:
![]() ,(16)
,(16)
valoarea functiei in punctul b, f(b), conform (9) corespunde tot unui punct de minim local.
Conditiile (15), (16) au devenit conditii de necesitate pentru un minim.
Minimul (maximul) global este cel mai mic (mare) minim (maxim) local sau una din valorile functiei la capetele intervalului de definitie.
Pentru cazul considerat (fig.5), punctele de minim local sunt a, m1, b, iar minimul global este b.
Concluzie: pentru functii definite pe un interval (corespunzator cazurilor reale din tehnica), pentru determinarea extremului global trebuie evaluata functia in punctele de extrem local si la extremitatile intervalului de definitie, conditia de suficienta ramanand relatia (3) pentru un minim, respectiv (6) pentru un maxim.
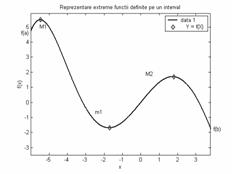
Fig.5 Functie reala definita pe un interval.
Procedand in acelasi mod ca in 2.2, pentru punctul M1 corespunzator functiei din fig. 6, sunt indeplinite conditiile:
![]() (17)
(17)
adica, la stanga punctului M1 derivata este pozitiva si functia crescatoare, iar
![]() , (18)
, (18)
f(x) fiind descrescatoare.
Avand indeplinite conditiile de necesitate (7) si (8) pentru punctul M1, (17) si (18), punctul M1 este un punct de maxim local.
Analizand asemanator punctul m2, pe baza conditiilor de necesitate (9), (10) punctul m2 este un punct de minim local.
Pe baza evaluarii functiei f(x) in punctele potentiale de extrem, din fig. 6 reiese ca maximul global este in punctul M1, iar minimul global al functiei se atinge in punctul m2.
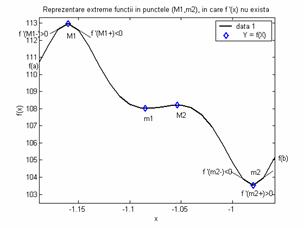
Fig.6 Reprezentare extreme in puncte in care derivata nu exista.
Justificarea matematica a conditiilor necesare de minim (9),(10) se poate realiza utilizand metoda pertubatiilor, metoda inventata de Lagrange.
Ipoteza: Fie x* un punct de minim al functiei f(x), punctul x* apartinand intervalului (a, b).
Daca pentru un oarecare e >0 suficient de mic inegalitatea
![]() (19)
(19)
este satisfacuta, atunci suma
![]() (20)
(20)
se va numi perturbatie a lui x*.
Valoarea functiei f in punctul x* trebuie sa satisfaca conditia de minim (2) fata de orice alt punct din intervalul (a,b), adica si fata de perturbatia (20):
![]() (21)
(21)
Din definitia derivatei, presupunand ca aceasta exista, se poate scrie:
![]() (22)
(22)
termenul de corectie o(Dx) indeplinind conditia
![]() (23)
(23)
Deci, valoarea functiei in perturbatia (20) poate fi scrisa, prin aproximare, sub forma:
![]() (24)
(24)
Presupunand f (x*)>0 pentru Dx < 0, relatia (24) conduce la urmatorul rezultat:
![]() , (25)
, (25)
care contrazice ipotezei de minim (21). Prin urmare,
![]() (26)
(26)
este conditia necesara de minim local.
Urmand acelasi rationament pentru Dx > 0, se obtine
![]() , (27)
, (27)
constituind cea de a doua conditie necesara de minim local.
Concluzii
Din (26), (27) daca nu exista f '(x) in punctul de minim x*, reiese ca derivata f '(x) isi schimba semnul la trecerea prin acesta.
Pentru mici modificari (perturbatii) in jurul lui x au loc mici modificari in f(x), modificari ce se aproximeaza printr-un termen care depinde de derivata de ordinul I, f (x).
In cazul in care derivata exista, conditia suficienta de minim local o constituie conditia f (x)>0.
Un minim global poate fi un minim local, dar reciproca nu este valabila.
Metoda generala de determinare a minimului global ramane relatia (3).
Problema care se formuleaza este de determinare a minimului pentru o functie reala f care depinde de mai multe variabile.
Utilizand rationamentul din subparagraful 2.1, aplicat unui vector de n componente, x de n componente x1, x2,, xn se pot deduce conditiile de minim local, respectiv global.
Un vector x*=[x*1 x*2 x*n]T, din An se numeste minim local al functiei f daca exista un e>0, suficient de mic, astfel incat pentru oricare vector x aflat intr-o vecinatate a lui x*, adica:
![]() (28)
(28)
f(x*) nu depaseste valoarea lui f(x):
![]() (29)
(29)
Un vector x* din An se numeste minim global (absolut) al functiei f daca
![]() (30)
(30)
pentru toti x din An
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3202
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved