| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
FORME BILINIARE. FORME PATRATICE
1 Forme biliniare
Multe probleme ale geometriei, analizei, fizicii si tehnicii conduc la forme biliniare, hermitiene sau patratice.
Distanta de la un punct M la origine este o forma patratica de coordonatele punctului M ; ecuatia unei sfere in coordonate omogene este o forma patratica in coordonate, expresia analitica a energiei cinetice, asa cum intervine ea, de exemplu, in ecuatiile lui Lagrange, este o forma patratica.
Definitia t1. Fie V un spatiu vectorial
peste K. O functie de doua variabile vectoriale cu valori in campul K,![]() se numeste forma
biliniara sau tensor covariant de ordinul doi pe V daca
este liniara in raport cu fiecare variabila, adica daca
se numeste forma
biliniara sau tensor covariant de ordinul doi pe V daca
este liniara in raport cu fiecare variabila, adica daca
![]() (t1)
(t1)
![]() (t2)
(t2)
Exemplu. Produsul scalar definit pe un spatiu vectorial real este o forma biliniara, in timp ce produsul scalar definit pe un spatiu vectorial complex nu este o forma biliniara.
Teorema t1. Fie ![]() o baza arbitrara in V.
O forma biliniara
o baza arbitrara in V.
O forma biliniara ![]() este complet determinata daca se cunosc valorile sale
este complet determinata daca se cunosc valorile sale ![]() pe produsul cartezian
pe produsul cartezian ![]()
Demonstratie. Fie x,y arbitrari din V,
![]()
tinand seama de (1) si (2) avem
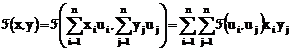
Expresia obtinuta pentru ![]()
![]() (t3)
(t3)
se numeste
expresia analitica a formei biliniare ![]() . Ea arata ca o forma biliniara este unic determinata daca se
cunosc cele
. Ea arata ca o forma biliniara este unic determinata daca se
cunosc cele ![]() numere din K
numere din K
![]() (t4)
(t4)
numite coeficientii formei biliniare in baza B.
Matricea
![]() (t5)
(t5)
de elemente ![]() se numeste matricea
formei biliniare
se numeste matricea
formei biliniare ![]() in baza B .
in baza B .
Daca utilizam matricele coloana
![]()
asociate vectorilor x si y , atunci expresia analitica a
formei biliniare ![]() poate fi scrisa sub forma matriceala
poate fi scrisa sub forma matriceala
![]() (t6)
(t6)
Forma
biliniara ![]() se numeste nedegenerata (degenerata) daca matricea sa este nesingulara (singulara).
Rangul formei biliniare
se numeste nedegenerata (degenerata) daca matricea sa este nesingulara (singulara).
Rangul formei biliniare ![]() este rangul matricei
A.
este rangul matricei
A.
Definitia t2. Forma biliniara ![]() se numeste simetrica
daca
se numeste simetrica
daca ![]() . Daca
. Daca ![]() se numeste forma
biliniara
se numeste forma
biliniara
antisimetrica.
Teorema t2 O forma biliniara ![]() este simetrica (antisimetrica) daca si numai daca matricea
formei intr-o baza a spatiului este simetrica (antisimetrica).
este simetrica (antisimetrica) daca si numai daca matricea
formei intr-o baza a spatiului este simetrica (antisimetrica).
Demonstratie. Presupunem ca ![]() este o forma simetrica:
este o forma simetrica:
![]()
in particular ![]() cu
cu![]() apartinand bazei
apartinand bazei ![]() din V. Cu notatiile
(4)
din V. Cu notatiile
(4) ![]() adica matricea A este simetrica
adica matricea A este simetrica ![]() Reciproc, daca A este
simetrica atunci
Reciproc, daca A este
simetrica atunci ![]() avem
avem
![]()
deci forma ![]() este simetrica .
este simetrica .
Teorema t3. Fie o forma biliniara ![]() data in baza B.
data in baza B.![]()
Daca ![]() este matricea de trecere de la baza
este matricea de trecere de la baza ![]() la baza
la baza ![]() din
din![]() , iar
, iar ![]() sunt matricele lui
sunt matricele lui ![]() in cele doua baze respectiv, atunci
in cele doua baze respectiv, atunci
![]() (t7)
(t7)
Demonstratie. In noua baza ![]() avem
avem
![]() (t8)
(t8)
Fie ![]() matricea formei in
aceasta baza :
matricea formei in
aceasta baza : ![]()
Notam ![]() Atunci
Atunci
![]() (t9)
(t9)
Folosind acum si relatiile de legatura dintre X si X', Y si Y' anume relatiile X = CX', Y =CY' din expresia
![]()
obtinem
![]() (t10)
(t10)![]()
Comparand
cele doua expresii (9) si (10) ale lui ![]() obtinem
obtinem
![]() (t11)
(t11)
Definitia t3. ![]() o forma biliniara
simetrica. Multimea
o forma biliniara
simetrica. Multimea ![]() se numeste nucleul
formei biliniare.
se numeste nucleul
formei biliniare.
Propozitia tt Nucleul formei biliniare este un subspatiu vectorial al lui V.
t2. Forme patratice
Consideram
un spatiu vectorial V peste campul K si o forma biliniara simetrica ![]() .
.
Definitia tt Functia ![]() definita prin egalitatea
definita prin egalitatea
![]() (t12)
(t12)
se numeste forma patratica asociata formei biliniare simetrice ![]() iar
iar ![]() se numeste forma
polara sau forma dedublata a lui
se numeste forma
polara sau forma dedublata a lui ![]() .
.
Exemplu. Forma patratica corespunzatoare produsului scalar real este patratul normei euclidiene
![]()
Observam ca forma patratica ![]() se obtine din forma biliniara simetrica data
se obtine din forma biliniara simetrica data ![]() punand y =x. Invers,
determinarea formei polare din forma patratica data
punand y =x. Invers,
determinarea formei polare din forma patratica data ![]() se face cu ajutorul relatiei
se face cu ajutorul relatiei
![]() (t13)
(t13)
Pentru a
se obtine (13) se exprima ![]() in functie de forma
simetrica
in functie de forma
simetrica ![]()
![]()
Cum ![]() avem relatia
avem relatia
![]()
care implica (13). Pentru a gasi expresia analitica a
formei patratice ![]() punem y = x, adica yi
= xi in expresia analitica a formei biliniare simetrice (3). Tinand
seama de notatia (4) a coeficientilor formei biliniare in baza
obtinem
punem y = x, adica yi
= xi in expresia analitica a formei biliniare simetrice (3). Tinand
seama de notatia (4) a coeficientilor formei biliniare in baza
obtinem
![]() (t14)
(t14)
Din(14) rezulta ca rangul formei patratice ![]() coincide cu rangul formei biliniare simetrice asociate lui
coincide cu rangul formei biliniare simetrice asociate lui ![]() .
.
Definitia t5. Fie ![]() o forma biliniara
simetrica si
o forma biliniara
simetrica si ![]() forma patratica
asociata. Vectorii x,y se numesc ortogonali in raport cu
forma patratica
asociata. Vectorii x,y se numesc ortogonali in raport cu ![]() (sau
(sau ![]() ) daca
) daca
![]() (x,y) =0.
(x,y) =0.
Definitia t6. Fie ![]() un spatiu vectorial al
lui V. Multimea
un spatiu vectorial al
lui V. Multimea ![]() se numeste complementul ortogonal al lui U in V fata de
se numeste complementul ortogonal al lui U in V fata de ![]() .
.
Definitia t7. Fie ![]() o forma biliniara
simetrica. O baza , se numeste ortogonala in raport cu forma
o forma biliniara
simetrica. O baza , se numeste ortogonala in raport cu forma ![]() daca
daca
![]() (t15)
(t15)
adica oricare doi vectori ei sunt ortogonali
fata de forma ![]() . Cum
. Cum ![]() , rezulta ca, in raport cu o baza ortogonala ,
matricea formei este diagonala.
, rezulta ca, in raport cu o baza ortogonala ,
matricea formei este diagonala.
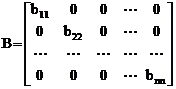 (t16)
(t16)
Notand bii
= bi, i=1,,n, expresiile analitice ale formei biliniare ![]() si formei patratice
asociate
si formei patratice
asociate ![]() , in baza ortogonala ,
devin:
, in baza ortogonala ,
devin:
![]() (t17)
(t17)
Aceste expresii se numesc expresii canonice
corespunzatoare formei biliniare simetrice ![]() si respectiv formei
patratice
si respectiv formei
patratice ![]() . Se spune in acest caz ca forma patratica
. Se spune in acest caz ca forma patratica ![]() (respectiv forma
biliniara
(respectiv forma
biliniara ![]() ) a fost redusa la expresia canonica .
) a fost redusa la expresia canonica .
t3. Reducerea formelor patratice si a celor biliniare simetrice la expresia canonica
Metoda lui GAUSS
Aceasta metoda opereaza asupra coordonatelor . Mai precis, dandu-se o forma patratica (14), se cauta o transformare liniara, nesingulara de matrice
![]()
astfel incat forma patratica sa se reduca la expresia canonica
![]()
Vom arata
mai intai ca daca in forma patratica ![]() toti coeficientii aij
sunt nuli (deci
toti coeficientii aij
sunt nuli (deci ![]() nu contine nici un
patrat) se poate determina o transformare liniara nesingulara astfel incat
forma
nu contine nici un
patrat) se poate determina o transformare liniara nesingulara astfel incat
forma ![]() sa contina un patrat.
Intr-adevar, sa
sa contina un patrat.
Intr-adevar, sa
consideram ca ![]() , de exemplu
, de exemplu ![]() . In acest caz efectuam transformarea liniara nesingulara
. In acest caz efectuam transformarea liniara nesingulara
x1 = y1 , x2 = y2 - y3 , x3 =y2 +y3 , x4 = y4,,xn = yn
Determinantul transformarii este

deci transformarea este nesingulara. Atunci
![]()
Deci cazul ![]() se reduce la cazul cand exista cel putin un patrat.
se reduce la cazul cand exista cel putin un patrat.
Fara a restrange generalitatea metodei, presupunem ![]() . Forma patratica
. Forma patratica ![]() se scrie acum punand in evidenta toti termenii care contin
variabila x1:
se scrie acum punand in evidenta toti termenii care contin
variabila x1:
![]()
unde Q(x) nu mai contine variabila x1; patratul se formeaza astfel :
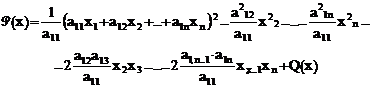
sau echivalent
![]()
unde
![]()
Determinantul
acestei transformari liniare este egal cu ![]() ;
;
Analog se procedeaza la formarea unui patrat pentru
![]()
etc.;
Dupa cel
mult n-1 de astfel de operatii obtinem expresia canonica a lui ![]() . Transformarea liniara este egala cu produsul
transformarilor nedegene-
. Transformarea liniara este egala cu produsul
transformarilor nedegene-
rate .
Aplicatii rezolvate
Aplicatia 1
Sa se reduca urmatoarele forme patratice la expresia canonica prin metoda Gauss :
a) ![]()
b) ![]()
Rezolvare :
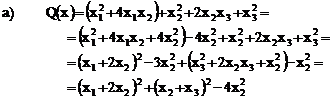
Fie transformarea :
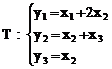
![]()
Signatura este (2,+1,0) .
b) ![]()
Fie transformarea :
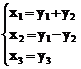
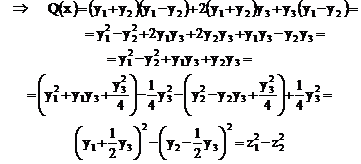
Signatura : (1,1,1).
Aplicatia 2
Sa se aduca la expresia canonica folosind metoda valorilor proprii urmatoarea forma patratica :
![]()
Matricea
este 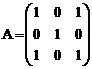
Valorile proprii sunt radacinile ecuatiei
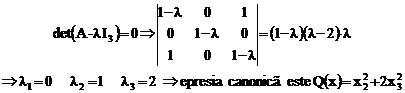
Signatura (2,0,1) .
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2853
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved