| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Inegalitati fundamentale in triunghi
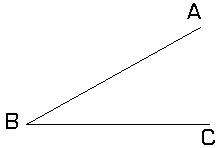
Definitia II.1.1: Spunem ca segmentul [AB] este mai mic decat segmentul [CD] daca masura segmentului [AB] este mai mica decat masura segmentului [CD] si scriem [AB]<[CD] daca AB<CD sau daca AB<CD (fig. II.1.1) .
 Definitia
II.1.2: Spunem ca
Definitia
II.1.2: Spunem ca ![]() este mai mic decat
este mai mic decat ![]() daca masura
unghiului
daca masura
unghiului ![]() este mai mica
decat masura unghiului
este mai mica
decat masura unghiului ![]() si scriem:
si scriem: ![]() daca
daca ![]() (fig. II.1.2)
(fig. II.1.2)
![]()
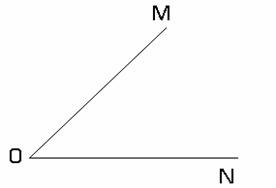
fig.II.1.1
fig.II.1.2
Definitia II.1.3: Un unghi se numeste exterior al unui triunghi daca este adiacent cu unul dintre unghiurile triunghiului si suplementar cu el.
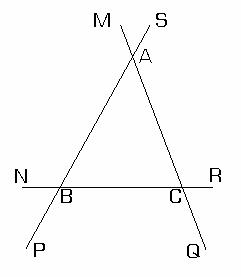
fig.II.1.3
In fig.II.1.3; (BN si (BC sunt semidrepte opuse, unghiurile ![]() si
si ![]() sunt adiacente si
suplementare, iar
sunt adiacente si
suplementare, iar ![]() este unghi al
triunghiului, deci unghiul
este unghi al
triunghiului, deci unghiul ![]() este unghi exterior
triunghiului ABC.
este unghi exterior
triunghiului ABC.
De asemenea, unghiurile ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() sunt unghiuri
exterioare triunghiului ABC.
sunt unghiuri
exterioare triunghiului ABC.
Teorema II.1.1: (Teorema unghiului exterior).
Un unghi exterior al unui triunghi este mai mare decat oricare dintre unghiurile triunghiului, neadiacent cu acel unghi.
Demonstratie:
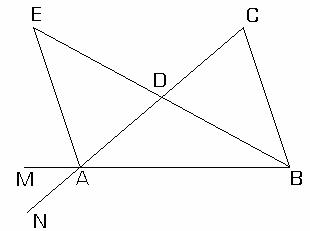 Fie triunghiul ABC (fig.II.1.4). Unghiurile
Fie triunghiul ABC (fig.II.1.4). Unghiurile ![]() si
si ![]() sunt exterioare
triunghiului ABC, unde
sunt exterioare
triunghiului ABC, unde ![]() . Se va arata ca:
. Se va arata ca: ![]() .
.
Fie D mijlocul segmentului (AC) si
![]() astfel incat
astfel incat ![]() .
.
Punctele E si M sunt de aceeasi
parte a dreptei AC, iar E si D sunt
de aceeasi parte
a dreptei AM, deci ![]() .
.
Rezulta ca: ![]() .
.
Dar ![]()
(unghiuri opuse la varf) si ![]()
rezulta ca ![]() (cazul L.U.L.)
(cazul L.U.L.)
De aici obtinem ![]() si, fig.II.1.4
si, fig.II.1.4
 tinand cont ca
tinand cont ca ![]() , deducem ca
, deducem ca ![]() adica
adica ![]() .
.
Se va arata acum ca ![]() .
.
Fie P mijlocul segmentului (AB) si ![]()
astfel incat ![]() (fig.II.1.5).
(fig.II.1.5).
Punctele Q si N sunt de aceeasi parte
a dreptei AB, iar Q si P de aceeasi
parte a dreptei AN. Deci ![]()
rezulta ca ![]() .
.
Dar ![]() si
si
![]() ceea ce implica
congruenta
ceea ce implica
congruenta
triunghiului APQ cu triunghiul BPC.
fig.II.1.5
De aici rezulta ca ![]()
![]() dar
dar ![]() prin urmare avem
prin urmare avem ![]() adica
adica ![]()
Cum ![]() (opuse la varf)
obtinem
(opuse la varf)
obtinem ![]() . Deci am demonstrat ca
. Deci am demonstrat ca ![]() si
si ![]() .
.
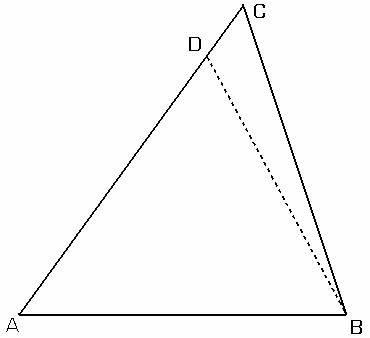
Teorema II.1.2:Intr-un triunghi cu doua laturi necongruente, laturii cu lungimea mai mare i se opune unghiul cu masura cea mai mare.
 Demonstratie:
Demonstratie:
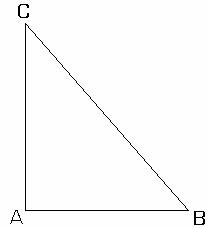
Fie triunghiul ABC cu AC>AB (fig.II.1.6).
Se considera punctul ![]() astfel
astfel
incat ![]() . Atunci triunghiul ABD
. Atunci triunghiul ABD
este triunghi isoscel si ![]() .
.
Dar ![]() este unghi exterior
triunghiului
este unghi exterior
triunghiului
BDC si folosind teorema II.1.1 obtinem ca
![]() . Rezulta ca
. Rezulta ca ![]()
iar cum ![]() avem
avem ![]() si
si
deci ![]() Prin urmare,
Prin urmare,
![]()
ceea ce implica ![]() .
.
fig.II.1.6
Teorema II.1.3:
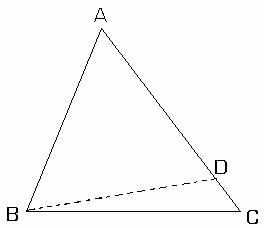
Intr-un triunghi cu doua unghiuri necongruente, unghiului cu masura mai mare i se opune latura cu lungimea mai mare.
 Demonstratie:
Demonstratie:
Fie triunghiul ABC cu ![]()
(fig.II.1.7). Se va demonstra ca AC>AB.
Consideram punctul ![]() astfel incat
astfel incat
![]() . Deci triunghiul ABD este isoscel,
. Deci triunghiul ABD este isoscel,
de unde rezulta ca ![]() .
.
Dar ![]()
![]() .
.
Deci ![]() . Prin urmare,
. Prin urmare,
![]() ceea ce implica
AD<AC si cum
ceea ce implica
AD<AC si cum
![]() obtinem AB<AC. fig.II.1.7
obtinem AB<AC. fig.II.1.7
 Observatie: In demonstratie s-a tinut cont ca in
triunghiul ABC avem
Observatie: In demonstratie s-a tinut cont ca in
triunghiul ABC avem ![]() si
si ![]()
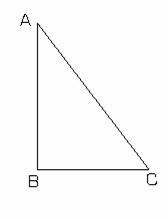
Teorema II.1.4:
Intr-un triunghi dreptunghic, lungimea ipotenuzei este
mai mare decat lungimea oricarei catete.
Demonstratie:
Fie triunghiul ABC in care ![]()
(fig.II.1.8). Cum ![]() tinand
tinand
cont de teorema II.1.3 obtinem BC>AB si BC>AC.
fig.II.1.8
Teorema II.1.5:
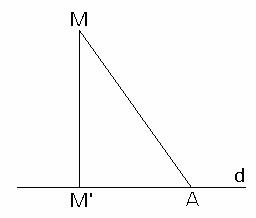 Fie o dreapta d inclusa intr-un plan
Fie o dreapta d inclusa intr-un plan
![]() si un punct
si un punct ![]() astfel incat
astfel incat ![]() . Daca notam cu
. Daca notam cu ![]() proiectia
punctului M pe dreapta d atunci pentru orice
proiectia
punctului M pe dreapta d atunci pentru orice  are loc relatia
are loc relatia ![]() .
.
Demonstratie:
Fie ![]() si
si ![]() , astfel incat
, astfel incat
![]() astfel incat
astfel incat ![]()
si  . Se formeaza triunghiul
. Se formeaza triunghiul
dreptunghic ![]() cu
cu ![]() (fig.II.1.9).
(fig.II.1.9).
Conform teoremei II.1.4, obtinem![]() .
.
fig.II.1.9
Definitia II.1.4: Se numeste distanta de la un punct la o dreapta, careia nu ii apartine, cea mai mica distanta dintre acel punct si punctele dreptei.
Observatie: Din cele de mai sus rezulta ca distanta de la un punct la o dreapta este distanta dintre acel punct si piciorul perpendicularei duse din acel punct la acea dreapta si se noteaza:
![]()
![]() si
si ![]() astfel incat
astfel incat ![]() .
.
Teorema II.1.6:
Dintre doua oblice duse dintr-un punct pe aceeasi dreapta, cea mai indepartata de piciorul perpendicularei duse din acel punct are lungimea cea mai mare.
Demonstratie:
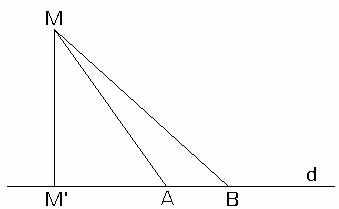 Fie o dreapta d inclusa intr-un plan
Fie o dreapta d inclusa intr-un plan
![]() ,
, ![]() astfel incat
astfel incat ![]() si
si ![]() .
.
Cazul a): A se afla intre ![]() si B
(fig.II.1.10).
si B
(fig.II.1.10).
Deoarece ![]() este unghi exterior
este unghi exterior
![]() avem:
avem: ![]()
Prin urmare, ![]() si in
si in
![]() si utilizand
si utilizand
teorema II.1.3 obtinem MB>MA.
fig.II.1.10
Cazul b): ![]() se afla intre A
si B (fig.II.1.11)
se afla intre A
si B (fig.II.1.11)
Consideram cazul in care ![]() . Fie
. Fie ![]() astfel incat
astfel incat ![]() .
.
Triunghiurile ![]()
![]() sunt triunghiuri
congruente si deci
sunt triunghiuri
congruente si deci ![]() Utilizand cazul a) obtinem:
Utilizand cazul a) obtinem: ![]()
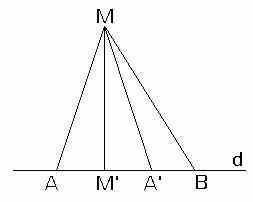
fig.II.1.11
Teorema II.1.7:
 Suma lungimilor a doua laturi ale unui
triunghi este mai mare decat lungimea celei de-a treia laturi.
Suma lungimilor a doua laturi ale unui
triunghi este mai mare decat lungimea celei de-a treia laturi.
Demonstratie:
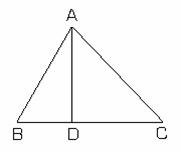
fig.II.1.12 fig.II.1.13 fig.II.1.14
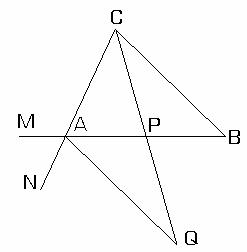
Cazul 1. Fie triunghiul ABC si ![]() astfel incat
astfel incat ![]() . Presupunem ca
. Presupunem ca ![]() si
si ![]() sunt unghiuri
ascutite (fig.II.1.12).
sunt unghiuri
ascutite (fig.II.1.12).
Prin urmare, punctul ![]() , astfel incat
, astfel incat ![]() . In triunghiul ADB,
. In triunghiul ADB, ![]() iar in triunghiul ADC,
iar in triunghiul ADC,
![]() , utilizand teorema II.1.3, deducem ca
, utilizand teorema II.1.3, deducem ca ![]() si
si ![]() , ceea ce implica:
, ceea ce implica: ![]() adica
adica ![]() .
.
Caz 2. Presupunem ca ![]() (fig.II.1.13).
Tinand cont de teorema II.1.3 avem
(fig.II.1.13).
Tinand cont de teorema II.1.3 avem ![]() in triunghiul ABC.
Prin urmare
in triunghiul ABC.
Prin urmare ![]() .
.
Caz 3. Presupunem ca ![]() (fig.II.1.14). Utilizand
teorema II.1.3, obtinem
(fig.II.1.14). Utilizand
teorema II.1.3, obtinem ![]() si, deci
si, deci ![]()
Teorema II.1.8:
Se considera triunghiurile ![]() si
si ![]() astfel incat
astfel incat ![]() si
si ![]() . In aceste conditii, daca
. In aceste conditii, daca ![]() atunci
atunci ![]() .
.
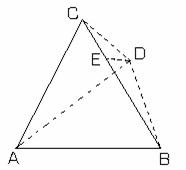 Demonstratie:
Demonstratie:
fig.II.1.15 fig.II.1.16
Construim punctul D in
semiplanul lui C, fata de AB, astfel incat triunghiurile ![]() si ABD sa
fie congruente (cazul L.L.L.:
si ABD sa
fie congruente (cazul L.L.L.: ![]() ) (fig.II.1.16).
) (fig.II.1.16).
Din ipoteza ![]() de unde rezulta
ca triunghiul ACD este isoscel
de unde rezulta
ca triunghiul ACD este isoscel ![]() si
si ![]() . Deci si bisectoarea
. Deci si bisectoarea ![]() va fi situata in
interiorul unghiului
va fi situata in
interiorul unghiului ![]() . Prin urmare, aceasta va intersecta segmentul (BC) intr-un
punct E si
. Prin urmare, aceasta va intersecta segmentul (BC) intr-un
punct E si ![]() . Rezulta ca
. Rezulta ca ![]() dar in triunghiul BED
avem
dar in triunghiul BED
avem ![]() conform teoremei
II.1.7 si deci
conform teoremei
II.1.7 si deci ![]() de unde obtinem
de unde obtinem ![]() .
.
Corolar II.1.8:
Daca triunghiurile ![]() si
si ![]() au
au ![]() si
si ![]() atunci
atunci ![]() .
.
Demonstratie:
Presupunem, prin absurd, ca in conditiile din ipoteza
vom avea ![]() .
.
Cazul 1. Daca ![]() tinand cont
ca
tinand cont
ca ![]() si
si ![]() deducem ca
triunghiurile
deducem ca
triunghiurile ![]() si
si ![]() sunt congruente, de
unde
sunt congruente, de
unde ![]() ceea ce contrazice
ipoteza.
ceea ce contrazice
ipoteza.
Cazul 2. Daca ![]() si avand in
vedere faptul ca
si avand in
vedere faptul ca ![]() iar
iar ![]() conform teoremei
II.1.7 obtinem
conform teoremei
II.1.7 obtinem ![]() ceea ce contrazice
ipoteza. Prin urmare, ramane adevarata doar situatia
ceea ce contrazice
ipoteza. Prin urmare, ramane adevarata doar situatia ![]() .
.
Teorema II.1.9: (A doua teorema a lui Grelu)
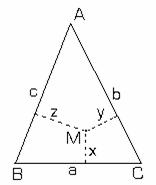 Punctul lui Lemaine este punctul pentru care suma
patratelor distantelor la laturile triunghiului este minima.
Punctul lui Lemaine este punctul pentru care suma
patratelor distantelor la laturile triunghiului este minima.
Demonstratie:
Fie ![]() si un punct M
situat in
si un punct M
situat in
interiorul triunghiului (fig.II.1.7)
Notam cu a=BC; B=AC; c=AB si cu
x=d(M;CB); y=d(M;AC); z=d(M;AB).
Din inegalitatea
Cauchy-Buniakowsky-Schwartz, se
obtine: ![]() fig.II.1.17
fig.II.1.17
dar ![]() , minimul
, minimul
obtinandu-se cand ![]() , dar egalitatea in inegalitatea Cauchy-Buniakowsky-Schwartz
se atinge cand
, dar egalitatea in inegalitatea Cauchy-Buniakowsky-Schwartz
se atinge cand ![]() , deci cand m este punctul lui Lemaine.
, deci cand m este punctul lui Lemaine.
Observatie: Punctul de concurenta a simedienelor (simetricele medianelor fata de bisectoare) se numeste punctul lui Lemaine al triunghiului.
Reamintim cateva identitati necesare in demonstrarea teoremei urmatoare enuntate de Svetoslav J. Bilchev si Emilia A Velikova in articolul: "ON A CERTAIN TRIANGLE TRANFORMATION AND SOME OF ITS APLICATIONS" - RAD IUGOSLAV AKAD YUAM UMJ, MAT[450], 9(1990), 69-76 dar care vor fi utile si in redactarea solutiilor aplicatiilor ce vor urma:
Fie un triunghi ABC in care notam cu a, b, c, S, r, R, ra, rb, rc, lungimile laturilor BC, AC, AB, semiperimetrul triunghiului ABC, aria triunghiului ABC, lungimea razei cercului inscris in triunghiul ABC si respectiv, lungimea razei cercului circumscris triunghiului ABC si lungimile razelor exinscrise. Au loc urmatoarele relatii:
II.1.1.1 ![]() si analoagele.
si analoagele.
II.1.1.2 ![]() formula lui Heron.
formula lui Heron.
II.1.1.3 ![]() .
.
II.1.1.4 ![]() .
.
II.1.1.5 ![]() .
.
II.1.1.6 ![]() .
.
II.1.1.7 ![]() .
.
II.1.1.8 ![]() .
.
II.1.1.9 ![]() .
.
II.1.1.10 ![]() .
.
II.1.1.11 ![]() .
.
II.1.1.12 ![]() .
.
II.1.1.13 ![]() .
.
II.1.1.14 ![]() .
.
II.1.1.15 ![]() .
.
Demonstratie II.1.1.1:
Din teorema cosinusului avem: ![]() dar
dar  ceea ce conduce la:
ceea ce conduce la: ![]() pe de alta parte
avem:
pe de alta parte
avem: 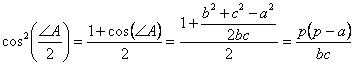 de unde obtinem:
de unde obtinem: ![]()
Demonstratie II.1.1.2:
Se stie ca aria unui triunghi se poate calcula
cu formula: ![]()
 Demonstratie II.1.1.3:
Demonstratie II.1.1.3:
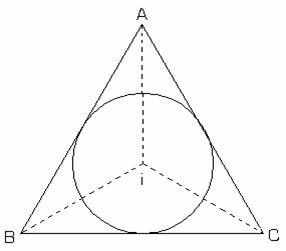
Notam cu i punctul de intersectie al
bisectoarelor triunghiului ABC (fig.II.1.18).
Inaltimile triunghiurilor AIB, AIC si BIC sunt
egale cu r si deci: ![]()
Demonstratie II.1.1.4:
Din teorema sinusurilor, ![]() .
.
Deci ![]() . fig.II.1.18
. fig.II.1.18
Demonstratie II.1.1.5:
Se stie ca aria unui triunghi se poate calcula cu ajutorul a uneia din formulele:
![]() iar din teorema
sinusurilor, deducem ca
iar din teorema
sinusurilor, deducem ca ![]() .
.
Prin urmare, ![]() ceea ce implica:
ceea ce implica: ![]() si deci
si deci ![]() .
.
Demonstratie II.1.1.6:
Din formula lui Heron, deducem: ![]() dar
dar ![]() de unde rezulta:
de unde rezulta:
![]() si deci:
si deci: ![]()
![]() .
.
Obtinem: ![]() si utilizand
identitatea precedenta, deducem:
si utilizand
identitatea precedenta, deducem:
![]() .
.
Demonstratie II.1.1.7:
Avem: ![]() si inlocuind in II.1.1.6 obtinem:
si inlocuind in II.1.1.6 obtinem: ![]() .
.
Demonstratie II.1.1.8:
Din identitatea: ![]() deducem, tinand
seama de identitatile demonstrate anterior ca:
deducem, tinand
seama de identitatile demonstrate anterior ca: ![]()
![]() .
.
Demonstratie II.1.1.9:
Avem: ![]()
![]()
![]()
![]() .
.
Demonstratie II.1.1.10:
Avem: ![]()
![]() . Prin urmare,
. Prin urmare, ![]() .
.
Demonstratie II.1.1.11:
Avem: ![]()
![]() si deci
si deci ![]() .
.
Demonstratie II.1.1.12:c
Avem: ![]()
![]() ceea ce implica:
ceea ce implica: ![]() . In mod analog,
. In mod analog,
![]() . Inmultind cele trei relatii, obtinem:
. Inmultind cele trei relatii, obtinem:
![]() , de unde rezulta:
, de unde rezulta: ![]() . Cum
. Cum ![]() si
si
![]() relatia
precedenta devine:
relatia
precedenta devine: ![]() care este
echivalenta cu:
care este
echivalenta cu: ![]() de unde rezulta
de unde rezulta ![]() .
.
Demonstratie II.1.1.13:
Am demonstrat anterior ca: ![]() ceea ce conduce la:
ceea ce conduce la:
![]()
![]() .
.
Demonstratie II.1.1.14:
![]()
![]() . Obtinem:
. Obtinem: ![]() deci
deci ![]() .
.
Demonstratie II.1.1.15:
![]()
![]()
![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3376
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved