| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Inegalitati intre laturi si arie
Aplicatia
II.5.1: Sa se arate ca in orice triunghi ABC are loc
inegalitatea: ![]()
Solutie:
Tinand cont de formula lui Heron pentru calculul ariei unui
triunghi, relatia din enunt este echivalenta cu: ![]() si daca
notam cu
si daca
notam cu ![]() ,
, ![]() ,
, ![]() , avem
, avem ![]() ,
, ![]() ,
, ![]() , iar noua egalitate va fi echivalenta cu:
, iar noua egalitate va fi echivalenta cu: ![]() , care este evidenta in baza inegalitatii:
, care este evidenta in baza inegalitatii: ![]() , cu egalitate in cazul triunghiului echilateral.
, cu egalitate in cazul triunghiului echilateral.
Aplicatia
II.5.2: Sa se arate ca in orice triunghi ABC are loc
inegalitatea: ![]() .
.
Solutie:
Din relatia ![]() deducem ca:
deducem ca: ![]()
![]() adica
adica ![]() .
.
 Aplicatia
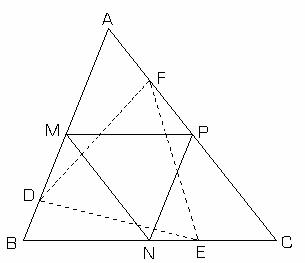
II.5.3 (Problema 0.110 G.M. nr.10/1980): In triunghiul ABC notam cu
M,N,P mijloacele laturilor
Aplicatia
II.5.3 (Problema 0.110 G.M. nr.10/1980): In triunghiul ABC notam cu
M,N,P mijloacele laturilor![]() ,
, ![]() ,
, ![]() si fie
si fie ![]() ,
, ![]() , si
, si ![]() . Sa se demonstreze ca:
. Sa se demonstreze ca: ![]() .
.
Solutie:
Fie triunghiul ABC si M,N,P mijloacele
laturilor ![]() ,
, ![]() ,
, ![]() , iar
, iar ![]() ,
,
![]() , si
, si ![]() (fig.II.5.1).
Consideram
(fig.II.5.1).
Consideram
![]() ;
; ![]() ;
; ![]() , evident
, evident
![]() .
.
![]() .
.
In mod analog: ![]() , iar
, iar ![]() .
.
Cum ![]() avem: fig.II.5.1
avem: fig.II.5.1
![]()
ceea ce implica:
![]() si, deci
si, deci ![]() , de unde rezulta:
, de unde rezulta:
![]() si prin urmare
si prin urmare ![]() . Notam cu
. Notam cu ![]() , obtinem:
, obtinem: ![]()
![]() si deci
si deci ![]() .
.
Pe de alta parte, ![]()
![]() si cum
si cum ![]() , iar
, iar ![]() , avand in vedere cele de mai sus,
, avand in vedere cele de mai sus, ![]() .
.
Aplicatia II.5.4: Sa se arate ca in orice triunghi ABC, cu lungimile laturilor a,b,c avem:
a) ![]() ,
, ![]() ,
, ![]()
b) ![]()
Solutie:
a) ![]() , ceea ce implica:
, ceea ce implica: ![]() , cu egalitate pentru
, cu egalitate pentru ![]() si
si ![]() . Celelalte doua inegalitati se obtin in
mod analog:
. Celelalte doua inegalitati se obtin in
mod analog:
b) ![]()
![]() si prin urmare
si prin urmare ![]() .
.
Aplicatia
II.5.5: Sa se arate ca in orice triunghi ABC avem: ![]()
Solutie:
![]() Deci
Deci ![]() cu egalitate daca
si numai daca :
cu egalitate daca
si numai daca :
![]() adica a=b=c.
adica a=b=c.
 Aplicatia
II.5.6: Fiind dat triunghiul ABC, alegem un punct oarecare pe una din
laturile sale si ducem din el paralele la celelalte laturi ale
triunghiului. Notam cu
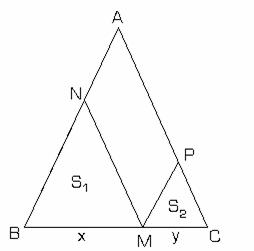
Aplicatia
II.5.6: Fiind dat triunghiul ABC, alegem un punct oarecare pe una din
laturile sale si ducem din el paralele la celelalte laturi ale
triunghiului. Notam cu ![]() ariile triunghiurilor
ce se formeaza prin construirea acestor paralele si cu S aria triunghiului
dat (fig.II.5.2) sa se arate ca este adevarata inegalitatea
:
ariile triunghiurilor
ce se formeaza prin construirea acestor paralele si cu S aria triunghiului
dat (fig.II.5.2) sa se arate ca este adevarata inegalitatea
: ![]()
Solutie:
![]() :
:
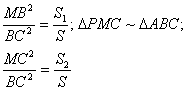
Fie MB=x, MC=y, MB+MC=BC; x+y=a
![]()
deci ![]()
fig.II.5.2
![]()
Avem egalitate pentru ![]() , deci M este la mijlocul lui [BC].
, deci M este la mijlocul lui [BC].
Prin absurd: ![]()
![]()
![]()
![]() contradictie.
Deci
contradictie.
Deci ![]() , BM=MC.
, BM=MC.
Aplicatia II.5.7: Fie ABC un triunghi. Sa se arate ca are loc inegalitatea:
![]() .
.
Solutie:
Scriind cunoscuta inegalitate a lui Euler: ![]() , obtinem:
, obtinem:
![]()
Folosind inegalitatea mediilor: 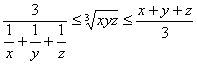 si inegalitatea
Caucky-Buniakovski-Schwartz:
si inegalitatea
Caucky-Buniakovski-Schwartz:
![]() ,
, ![]() avem:
avem:
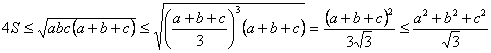 .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1534
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved