| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Inegalitati referitoare la laturile unui triunghi
Aplicatia II.2.1: Sa se demonstreze ca in orice triunghi ABC are loc relatia:
![]()
Solutie:
Tinand cont ca media aritmetica este mai mare sau
egala cu media armonica deducem ca:  de unde obtinem:
de unde obtinem: ![]() dar
dar ![]() .
.
Deci: ![]() cu egalitate in cazul
triunghiului echilateral. Pe de alta parte, tinand cont de teorema
II.1.7. obtinem:
cu egalitate in cazul
triunghiului echilateral. Pe de alta parte, tinand cont de teorema
II.1.7. obtinem: ![]() ceea ce implica:
ceea ce implica: ![]() adica
adica ![]() .
.
Din inegalitatile ![]() si
si ![]() obtinem
relatia din enunt.
obtinem
relatia din enunt.
Aplicatia II.2.2: Sa se demonstreze ca in orice triunghi ABC are loc inegalitatea:
![]() .
.
Solutie:
Fie triunghiul ABC in care notam cu ![]() . De asemenea notam cu
. De asemenea notam cu ![]() si
si ![]() . Prin urmare,
. Prin urmare,
![]() . Deci inegalitatea
. Deci inegalitatea ![]() este echivalenta
cu:
este echivalenta
cu: ![]() .
.
Aplicatia II.2.3: Sa se arate ca in orice triunghi ABC are loc inegalitatea:
![]() .
.
Solutie:
Notam cu ![]() . Avem:
. Avem: ![]()

![]() si deci
si deci ![]() cu egalitate in cazul
triunghiului echilateral.
cu egalitate in cazul
triunghiului echilateral.
Aplicatia II.2.4: Fie triunghiul dreptunghic ABC
cu ![]() Sa se arate
ca:
Sa se arate
ca:
![]() unde am notat cu
unde am notat cu ![]()
Solutie:
Fie triunghiul ABC cu ![]()
(fig.II.2.1). Notam cu ![]()
Avem ![]() si
si ![]() ,
,
conform aplicatiei II.2.1, ceea ce implica ![]() si
si ![]() ,
,
conform teoremei II.1.4. fig.II.2.1
Prin urmare, ![]() si
si ![]() , de unde rezulta
, de unde rezulta ![]() , ceea ce implica
, ceea ce implica ![]() , adica
, adica ![]() si deci
si deci ![]() .
.
Aplicatie II.2.5: Sa se arate ca in orice triunghi ABC are loc relatia:
![]()
Solutie:
Fie triunghiul ABC in care notam cu ![]() Se stie ca:
Se stie ca: ![]()
![]() si
si ![]() . Prin urmare,
. Prin urmare, ![]() de unde obtinem
de unde obtinem ![]()
![]() cu egalitate in cazul
triunghiului echilateral.
cu egalitate in cazul
triunghiului echilateral.
De asemenea se stie ca: ![]() in orice triunghi ceea
ce implica:
in orice triunghi ceea
ce implica: ![]()
Prin urmare, ![]() de unde rezulta:
de unde rezulta:
![]() , adica:
, adica: ![]()
![]() si obtinem:
si obtinem: ![]()
![]() .
.
Din inegalitatile ![]() si
si ![]() obtinem
relatia ce trebuia demonstrata.
obtinem
relatia ce trebuia demonstrata.
Aplicatia II.2.6: Sa se demonstreze ca in orice triunghi ABC are loc inegalitatea:
![]() .
.
Solutie:
Fie triunghiul ABC in care notam cu ![]() Atunci
Atunci ![]()
![]()
![]()
![]()
![]() conform teoremei
II.1.7.
conform teoremei
II.1.7.
Prin urmare: ![]() .
.
Aplicatie II.2.7: Sa se demonstreze ca in orice triunghi ABC are loc relatia:
![]()
Solutie:
Fie triunghiul ABC in care notam cu ![]() De asemenea,
notam cu:
De asemenea,
notam cu:
![]() . Deducem ca:
. Deducem ca: ![]()
![]() si
si ![]() . Prin urmare,
. Prin urmare, ![]()
![]()
Am tinut cont ca, deoarece: ![]() obtinem:
obtinem: ![]() si analoagele.
si analoagele.
Aplicatie
II.2.8: Sa se arate ca daca a,b,c sunt lungimile laturilor
unui triunghi ABC, atunci: ![]()
[G.M. nr. 1/1999]
Solutie:
Presupunem ca ![]() . Atunci:
. Atunci: ![]()
![]() .
.
Dar ![]() Conform relatiilor
Conform relatiilor ![]() si
si ![]() , inegalitatea din enunt este echivalenta cu:
, inegalitatea din enunt este echivalenta cu:
![]()
Notam cu ![]() obtinem:
obtinem: ![]() iar
iar ![]() si
si ![]() .
.
Relatia ![]() este echivalenta
cu:
este echivalenta
cu: ![]()
![]()
![]() care este
evidenta deoarece:
care este
evidenta deoarece: ![]() ,
, ![]() si
si ![]() . Egalitatea se verifica pentru
. Egalitatea se verifica pentru ![]()
Aplicatia II.2.9: Sa se demonstreze ca in orice triunghi ABC are loc relatia:
![]()
Solutie:
Notam cu ![]() avem:
avem: ![]() si
si ![]() Cum
Cum ![]()
![]()
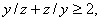 obtinem:
obtinem: ![]() adica:
adica: ![]() si, prin urmare,
si, prin urmare, ![]() cu egalitate in cazul
triunghiului echilateral.
cu egalitate in cazul
triunghiului echilateral.
Aplicatia
II.2.10: In orice triunghi ABC are loc inegalitatea: ![]() .
.
Solutie:
![]()
![]() cu egalitate in cazul
triunghiului isoscel cu
cu egalitate in cazul
triunghiului isoscel cu ![]() .
.
Se observa ca in mod asemanator, se pot demonstra si inegalitatile:
![]() si
si ![]() .
.
Observatie: Tinand cont de problema nr.7 pag 230 din G.M. nr.6/1983 si de articolul "Aplicatii ale inegalitatilor lui OPPENHEIN si ERDOS-MORDLL" publicat de Mircea Lascu in Revista Matematica din Suceava, nr.1/1991, putem sa demonstram urmatoarele aplicatii:
Aplicatia II.2.11 (G NEVELITIS): Sa se arate ca perimetrul triunghiului de arie 2 este mai mare decat 6.
Solutie:
Notand cu a,b,c laturile triunghiului ABC si cu ![]() inaltimile
corespunzatoare, avem:
inaltimile
corespunzatoare, avem: ![]() . Prin urmare,
. Prin urmare, ![]()
Din inegalitatea mediilor, avem:
![]() ;
; ![]() ;
; ![]() ;
;
Cum ![]() ;
; ![]() ;
; ![]() , deducem
, deducem ![]()
![]() ceea ce implica
ceea ce implica ![]() .
.
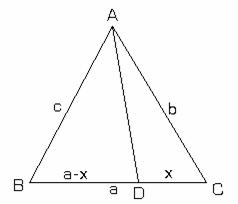 Aplicatia
II.2.12: Pe latura unui triunghi ABC se ia un punct oarecare D (fig.II.2.2)
Sa se demonstreze ca AD este mai mica decat semiperimetrul
triunghiului din care se scade BC:
Aplicatia
II.2.12: Pe latura unui triunghi ABC se ia un punct oarecare D (fig.II.2.2)
Sa se demonstreze ca AD este mai mica decat semiperimetrul
triunghiului din care se scade BC: ![]() .
.
Solutie:
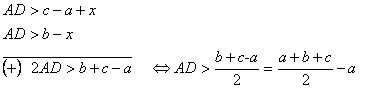
Deci, ![]()
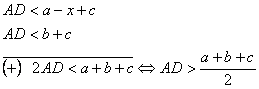 fig.II.2.2
fig.II.2.2
Deci, ![]() .
.
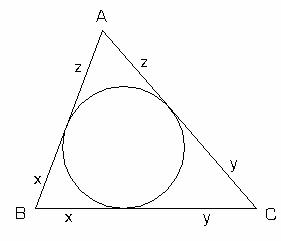
Aplicatia II.2.13: Fie ABC un triunghi oarecare (fig.II.2.3). Sa se arate ca au loc inegalitatile:
![]() .
.
Solutie:
![]() ;
; ![]() adevarat,
adevarat,![]()


![]()
![]()
![]()
![]()
![]() fig.II.2.3
fig.II.2.3
![]()
![]()
Aleg: ![]()
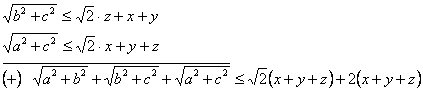
![]()
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4679
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved