| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Siruri si serii de elemente din ![]() (
(![]() ).
).
I
I.1) Sa se studieze natura urmatoarelor siruri si, atunci cand este cazul, sa se determine limitele corespunzatoare:
a)
![]() , unde
, unde ![]() ,
, ![]() si
si ![]() ;
;
b)
![]() , unde
, unde ![]() si
si ![]() ;
;
c)
![]() , unde
, unde 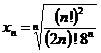 ,
, ![]() si
si ![]() ;
;
d)
![]() , unde
, unde 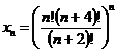 si
si ![]() ;
;
e)
![]() ,
, ![]() ,
, ![]() si
si ![]() ;
;
f)
![]() ,
, ![]() ,
, 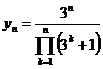 ;
;
g)
![]() , unde
, unde ![]() si
si ![]() ;
;
h)
![]() , unde
, unde ![]() si
si ![]() ;
;
i)
![]() , unde
, unde ![]() ,
, ![]() si
si ![]() ;
;
j)
![]() , unde
, unde 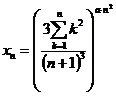 , cu
, cu ![]() , si
, si ![]() ,
, ![]() , cu
, cu ![]() .
.
k)
![]() , unde
, unde ![]() ,
, ![]() ,
,
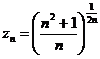 si
si ![]() ,
, ![]() .
.
a)
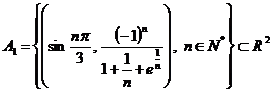 ;
;
b)
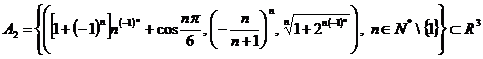 ;
;
c)
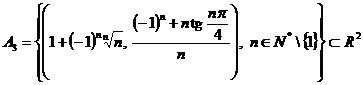 ;
;
d)
![]() .
.
II.1) Folosind diverse criterii de convergenta, sa se stabileasca natura seriilor de mai jos. Sa se calculeze apoi, ori de cate ori este posibil, sumele in cauza.
a)
![]() ;
;
b)
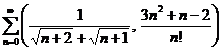 ;
;
c)
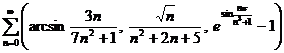 ;
;
d)
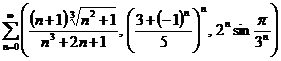 ;
;
e)
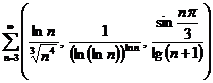 ;
;
f)
![]() ;
;
g)
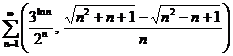 ;
;
h)
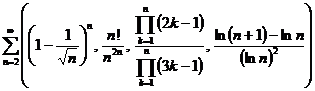 ;
;
i)
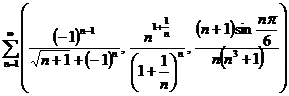 ;
;
j)
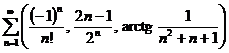 .
.
II.2) Sa se studieze, in raport cu parametrii implicati, natura urmatoarelor serii:
a)
![]() ;
;
b)
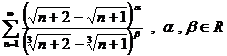 ;
;
c)
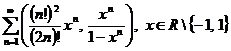 ;
;
d)
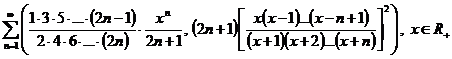 ;
;
e)
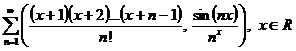 .
.
II.3) a) Fie ![]() o serie din R, cu
o serie din R, cu ![]() . Sa se arate ca seria
. Sa se arate ca seria ![]() are
are
aceeasi natura cu a celei date.
b)
Sa se demonstreze ca
daca seria ![]() , cu
, cu ![]() , este convergenta, atunci la fel este si seria
, este convergenta, atunci la fel este si seria ![]() .
.
c)
Sa se arate ca daca
seriile de numere reale ![]() si
si ![]() sunt convergente,
atunci seria
sunt convergente,
atunci seria ![]() este de asemenea
convergenta.
este de asemenea
convergenta.
III.1) Sa se determine ![]() , astfel incat, in
, astfel incat, in ![]() , punctul
, punctul ![]() sa
apartina multimii
sa
apartina multimii
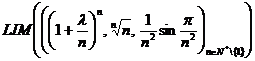 .
.
III.2) Fie ![]() un sir de
elemente din
un sir de
elemente din ![]() , unde d este o
metrica pe
, unde d este o
metrica pe ![]()
![]() . De
. De
asemenea, fie, ![]() . Sa se arate ca
. Sa se arate ca ![]() este un sir
Cauchy
este un sir
Cauchy
in ![]() , daca si numai daca sirul diametrelor
multimilor
, daca si numai daca sirul diametrelor
multimilor ![]() , adica
, adica ![]() , este
, este
convergent si are limita egala cu 0.
III.3) Fie A o submultime
nevida, compacta a spatiului metric ![]() si
si ![]() diametrul lui A,
diametrul lui A,
in raport cu distanta d.
Sa se arate ca exista ![]() si
si ![]() din A, astfel incat
din A, astfel incat ![]() .
.
III.4) Fie d o metrica pe ![]() si
si ![]()
![]() . Definim
. Definim ![]() .
.
Sa se arate ca un punct z este din ![]() daca si numai daca
daca si numai daca ![]() .
.
III.5) Fie ![]() si d o metrica pe
si d o metrica pe ![]() . Sa se demonstreze ca
. Sa se demonstreze ca ![]() ,
,
![]() , unde
, unde ![]() este
functia-distanta definita in exercitiul precedent.
este
functia-distanta definita in exercitiul precedent.
III.6) Fie d o distanta pe ![]()
![]() , in raport cu care
, in raport cu care ![]() este un spatiu
metric complet.
este un spatiu
metric complet.
De asemenea , fie o functie ![]() , astfel incat ,
pentru orice
, astfel incat ,
pentru orice ![]() , exista
, exista
![]() si are loc relatia :
si are loc relatia :
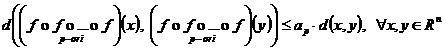 .
.
Sa
se arate ca daca seria ![]() este convergenta,
atunci f are un punct fix unic.
este convergenta,
atunci f are un punct fix unic.
F. Iacob
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2145
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved