| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Consideram ecuatia
f (x) = 0 (4.4)
unde f : I → R, iar I este un interval al axei reale.
Sa inlocuim ecuatia (4.4) printr-o ecuatie echivalenta de forma
![]() (4.5)
(4.5)
Definitie 4.5.1 Radacinile ecuatiei (4.5) se numesc puncte fixe ale lui φ.
Construim sirul de iteratii
![]() , pentru n = 0, 1, 2, ., (4.6)
, pentru n = 0, 1, 2, ., (4.6)
unde x0 este o valoare aproximativa initiala a radacinii care se cauta.
Teorema 4.5.1 Daca φ
: [a, b] → R (a, b![]() R, a < b) si indeplineste
urmatoarele conditii:
R, a < b) si indeplineste
urmatoarele conditii:
( α ) oricare ar fi ![]() rezulta
rezulta ![]()
( β ) exista q ![]() [0, 1) astfel incat oricare ar fi u1, u2
[0, 1) astfel incat oricare ar fi u1, u2 ![]() [a, b]
este indeplinita inegalitatea
[a, b]
este indeplinita inegalitatea
![]()
atunci avem:
a)
daca ![]() sirul
sirul ![]() generat de
relatia (4.6) este convergent;
generat de
relatia (4.6) este convergent;
b)
![]() este unica radacina a ecuatiei (4.4) pe [a, b].
este unica radacina a ecuatiei (4.4) pe [a, b].
Demonstratie.
a) Pentru doua
iteratii consecutive ![]() si
si ![]() , tinand
cont de relatiile ( α ) si ( β ) avem:
, tinand
cont de relatiile ( α ) si ( β ) avem:
![]() (4.7)
(4.7)
Inegalitatea (4.7) are loc pentru n = 1, 2, . si aplicand-o succesiv pentru aceste valori avem:
![]() , ( n
= 1, 2, .). (4.8)
, ( n
= 1, 2, .). (4.8)
Seria
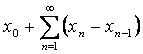
este absolut convergenta deoarece seria valorilor absolute ale termenilor sai este majorata de o serie geometrica de ratie q < 1, asa cum rezulta din relatia (4.8).
Fie Sn+1 suma partiala de ordin n+1 a seriei de mai sus. Rezulta ca
Sn+1 = xn
Deoarece seria este convergenta, rezulta ca si sirul sumelor partiale este convergent, adica
![]()
Din conditia ( β ) rezulta continuitatea functiei φ pe [a, b]. Deci sunt justificate urmatoarele egalitati:
![]()
adica ![]() verifica (4.5) si implicit pe (4.4).
verifica (4.5) si implicit pe (4.4).
Deoarece ![]() este un interval inchis, pentru n = 0, 1, 2, ., rezulta ca
este un interval inchis, pentru n = 0, 1, 2, ., rezulta ca ![]() .
.
b) Aratam, prin reducere la absurd, ca ecuatia (4.5) are solutie unica.
Fie x1, x2 doua solutii distincte ale ecuatiei (4.5). Din relatia ( β ) avem:
![]()
Ultima
inegalitate este imposibila deoarece ![]() iar 1 - q
> 0 ( din ( β)).
iar 1 - q
> 0 ( din ( β)).
Observatie 4.5.1 Putem inlocui conditia (β), pentru functia φ derivabila, prin inegalitatea
![]()
(acest fapt rezulta din teorema de medie a lui Lagrange).
Observatie 4.5.2 Teorema 4.5.1 este adevarata si pentru ![]() .
.
Observatie 4.5.3 Teorema 4.5.1 ne arata ca sirul ![]() dat de
egalitatea (4.6) converge oricum am alege pe
dat de
egalitatea (4.6) converge oricum am alege pe ![]() , adica
aceasta metoda este autocorectoare.
, adica
aceasta metoda este autocorectoare.
Teorema 4.5.2 Fie ![]() R avand semnificatia data de relatia (4.5).
Daca φ satisface conditiile:
R avand semnificatia data de relatia (4.5).
Daca φ satisface conditiile:
(γ) φ este derivabila in fiecare punct ![]()
(δ) ecuatia x = φ (x) are o radacina ![]() unde
unde ![]() iar
iar ![]()
(η) ![]() pentru orice
pentru orice ![]()
(σ) ![]()
atunci avem:
a)
toate
elementele sirului ![]() apartin
intervalului (a, b);
apartin
intervalului (a, b);
b)
sirul
![]() este
convergent si
este
convergent si ![]() ;
;
c)
![]() este unica solutie a ecuatiei (4.5) pe (a, b).
este unica solutie a ecuatiei (4.5) pe (a, b).
Demonstratie.
a)
Vom
demonstra, prin inductie, ca elementele sirului ![]() apartin
intervalului (a, b). Deoarece
apartin
intervalului (a, b). Deoarece ![]() , putem
calcula
, putem
calcula ![]() si avem, utilizand Teorema lui Lagrange:
si avem, utilizand Teorema lui Lagrange:
![]()
![]()
adica ![]() .
.
Presupunem ca ![]() si ca
si ca ![]() . Rezulta:
. Rezulta:
![]()
adica ![]() pentru n = 1, 2, . .
pentru n = 1, 2, . .
Observatie 4.5.4 Daca ![]() , sirul
aproximatiilor succesive este monoton
crescator sau descrescator dupa cum
, sirul
aproximatiilor succesive este monoton
crescator sau descrescator dupa cum ![]() .
.
Daca ![]() , atunci
sirul este oscilant in jurul radacinii
, atunci
sirul este oscilant in jurul radacinii ![]() .
.
Teorema 4.5.3 Evaluarea erorii sirului aproximatiilor succesive.
Daca ne situam in ipotezele Teoremei 4.5.1, atunci avem
![]()
Demonstratie. Fie p Є N si avem

Trecand la limita pentru p → ∞, avem:
![]()
Teorema 4.5.4 Fie δ Є R, δ > 0 si f : [x0 -δ, x0 + δ]
→ R o functie derivabila pe acest interval. Daca f satisface conditia ca ![]() unde
unde
![]()
atunci ecuatia f (x) = 0 are o singura radacina in intervalul [x0 -δ, x0 + δ].
Demonstratie. Este suficient sa demonstram acest fapt pentru f (x0) > 0, demonstratia pentru f (x0) < 0 fiind similara.
Deoarece m ≠ 0 rezulta ca f are acelasi semn pe [x0 -δ, x0 + δ], deci f este monotona pe acest interval.
Prin urmare f
isi atinge marginea inferioara exacta
intr-un punct ![]() care este unul din capetele intervalului.
care este unul din capetele intervalului.
Din teorema lui Lagrange avem:
![]() , unde
Є ( x0 -δ, x0 + δ ).
, unde
Є ( x0 -δ, x0 + δ ).
Tinand cont de faptul ca
![]() rezulta ca
rezulta ca ![]()
Deoarece
![]() si
si ![]()
avem
![]() sau
sau
![]() .
.
Distingem doua cazuri: 1) daca ![]() , atunci
, atunci ![]() ; 2) daca
; 2) daca ![]() si din
faptul ca
si din
faptul ca ![]() rezulta ca exista
rezulta ca exista ![]() astfel ca
astfel ca ![]() . (Teorema
lui Cauchy).
. (Teorema
lui Cauchy).
In incheiere dam un procedeu de trecere de
la ecuatia 4.4 la ecuatia 4.5 cu respectarea conditiei ![]() .
.
Sa presupunem ca f este strict crescatoare pe (α ,
β) adica ![]() pentru
pentru![]() Daca f este
strict descrescator, aplicam acelasi procedeu pentru functia - f.
Daca f este
strict descrescator, aplicam acelasi procedeu pentru functia - f.
Consideram functia
![]()
unde
λ Є R este un parametru real ce urmeaza a fi determinat
astfel ca ![]() .
.
Fie m1 si M1 doua constante astfel incat
![]()
Avem
![]()
sau tinand cont de relatia de mai sus rezulta
![]()
Deci putem alege
![]() si
si 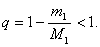
Exemplu 4.5.1 Sa se determine radacina pozitiva a ecuatiei
![]()
cu precizia ![]() .
.
Solutie.
Coeficientii ecuatiei, avand o singura variatiune de semn, rezulta ca ecuatia admite o singura radacina pozitiva si este singura reala, celelalte doua fiind complexe (deoarece f(-x) = 0 are numai permanente).
Scriem ecuatia sub forma
![]()
Deci
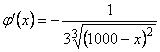
Consideram drept valoare aproximativa pe x0 = 10. Deoarece f (10) = 10 > 0 si f (9) < 0 urmeaza:
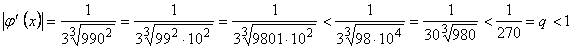
Formam sirul aproximatiilor succesive:
![]()
Deci
![]()
![]()
![]()
Programul pentru metoda aproximatiilor succesive
Programul determina solutia unei ecuatii de forma (4.4) in urmatoarele ipoteze:
- solutia este separata intr-un interval [a, b];
- functia este continua si derivabila pe intervalul [a, b].
Datele de intrare sunt: capetele intervalului in care se cauta solutia (a, b) si precizia dorita (epsilon). Functia si derivata ei sunt definite prin proceduri de tip functie.
In cadrul programului se determina
functia φ astfel incat ![]() . In acest
scop se calculeaza maximul valorii absolute a derivatei functiei f pe intervalul [a, b].
. In acest
scop se calculeaza maximul valorii absolute a derivatei functiei f pe intervalul [a, b].
Algoritmul care sta la baza programului urmareste determinarea iteratiei urmatoare atata timp cat diferenta intre doua iteratii succesive este mai mare decat precizia impusa.
# include <iostream .h>
# include <math .h>
# include <conio .h>
double f (double x)
double df (double x)
void main (void)
while (x <= b);
if (m1 = = 0)
t = 2;
else
}
while((t = =0)&& (pas>eps));}
if ( t = = 3)
cout<<"Solutia este x ="<<xc<<endl;
if ( t = = 0)
cout<<"Solutia aproximativa este x ="<<xc<<endl;
if ( t = = 2)
cout<<"Nu se poate aplica metoda aproximatiilor succesive!"<<endl;
}
getch ( );
}
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4724
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved