| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
In acest capitol vor fi prezentate o serie de metode deterministe de clasificare. Aceste metode sunt in esenta proceduri de optimizare a unor functii criteriu. Pentru construirea unei functii criteriu se admite ca fiecare clasa este reprezentata printr-un prototip geometric. Prototipurile pot fi punctuale, caz in care clasele au aproximativ forma sferica sau liniara, caz in care clasele au forma alungita. Functia criteriu reprezinta o masura a apartenentei sau a neapartenentei unei partitii a datelor la prototipurile claselor. Calitatea unei partitii este cu atat mai mare cu cat punctele fiecarei clase sunt mai grupate in jurul prototipului clasei.
O alta posibilitate pentru contruirea functiei criteriu este aceea de a utiliza matricile de imprastiere a datelor. Clasificarea optima va fi aceea in care imprastierea in interiorul fiecarei clase este minima (clasele sunt mai compacte) si imprastierea intre clase este mai mare (clasele sunt cat mai separate una de alta) .
Se studiaza doua metode puternice de analiza a datelor : Analiza Discriminanta (AD) si Analiza Componentelor Principale (ACP) . Se evidentieaza faptul ca AD si ACP pot servi pentru elaborarea unor tehnici de clasificare.
Fie X o multime de obiecte de clasificat. Cea mai generala masura de disimilaritate pe care o putem defini peste X este o functie D: X*X R care satisface axiomele:
D(x,y)³ x,yIX
D(x,x)=0 xIX
D(x,y)=D(y,x) x,yIX
Se admite ca X este multime de instruire (cunoastem pentru fiecare obiect din X clasa caruia el apartine) iar D este o masura de disimilaritate adecvata. In aceste conditii este de asteptat ca disimilaritatea dintre obiectele aceleiasi clase sa fie sensibil mai mica decat disimilaritatea dintre puncte aflate in clase diferite. In cazul cand datele sunt obiecte dintr-un spatiu euclidian vom considera metrica spatiului ca o masura a disimilaritatii.
Daca X si Y sunt puncte dintr-un spatiu euclidian d-dimensional
X = (x1, x2,,xd),
Y =(y1, y2,,yd),
atunci pentru orice numar real p³ se poate defini metrica:
d(X, Y)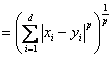 (1)
(1)
De fapt (1) reprezinta o familie infinita de matrici. Pentru p = 1 din (1) se obtine:
d(X, Y)![]() (2)
(2)
numita metrica absoluta sau distanta City Black.
Daca p = 2 se obtine distanta euclidiana :
d(X, Y)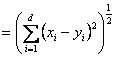 (3)
(3)
iar pentru p se obtine metrica valorii maxime :
d(X, Y)![]() (4)
(4)
Sa consideram ca valorile posibile ale caracteristicilor formelor de clasificat sunt in numar finit si fie d acest numar. In acest caz ca masura de disimilaritate se pot utiliza distantele Hamming si Lee.
Distanta Hamming dintre vectorii X si Y este data de numarul componentelor (pozitiilor) in care cei doi vectori difera. Ponderea Hamming a vectorului X, notata cu WH(X), se defineste ca fiind numarul de componente nenule ale lui X. Rezulta ca distanta Hamming dintre X si Y este egala cu ponderea Hamming a diferentei lor :
dH (X, Y)= WH(X, Y) (5)
Distanta Lee
Fie q un numar intreg, pozitiv, q³ si X = (x1, x2,,xd), cu xiI .
Ponderea Lee a vectorului X, notata cu WL(X), se defineste ca fiind:
WL(X)![]()
unde:
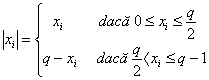
Distanta Lee a vectorilor X si Y se defineste ca fiind ponderea Lee a diferentei lor:
dL (X, Y)= WL(X- Y) (6)
Pentru q = 2 si q = 3 distantele Hamming si Lee coincid. Pentru q>3 avem:
dL (X, Y)³ dH (X, Y) X, Y
De asemenea pentru q = 2 avem
dH (X, Y)![]()
In cele ce urmeaza vom considera ca fiecare obiect de clasificat Xi se reprezinta ca un vector d-dimensional:
xi=( x1i, x2i, . . . ,xdi)
unde xji, specifica componenta j a vectorului xi .
Consideram o multime de obiecte X= , xiIRd
Vom nota cu m vectorul medie a datelor:
m=![]() (7)
(7)
Componenta mk a vectorului m este :
mk=![]()
si reprezinta valoarea medie a caracteristicii k. Daca ne raportam din nou la multimea de obiecte X atunci caracteristica i a lui X este
Xi
si deci vom putea scrie ca :
mi= MX i
unde cu M am notat operatorul valoare medie.
Cu aceasta putem sa definim dispersia valorilor in jurul valorii medii atat pentru:
caracteristica i
si sii= M(Xi - mi)2 (8)
caracteristicile i si k
sik= M(Xi - mi)(Xk - mk) (9)
Relatia (8) se mai poate
scrie ![]() din care rezulta imediat prin dezvoltarea
termenului din suma
din care rezulta imediat prin dezvoltarea
termenului din suma
![]() M(Xi2)-mi2
M(Xi2)-mi2
si deci
![]() (11)
(11)
Cu aceste observatii se poate defini matricea C(d,d) de componente sik ca reprezentand matricea de dispersie pentru multimea X de obiecte. In cadrul acestei matrici elementul sii va reprezenta imprastierea (dispersia) norului de obiecte in directia axei i a sistemului de coordonate .
Sa consideram acum un nor de obiecte
X=
al carui vector medie coincide cu originea spatiului, adica M(X) = 0. Ne propunem sa determinam dispersia (imprastierea) norului in directia vectorului u. Considerand ca obiectele prezinta 3 caracteristici de exemplu, devine posibila reprezentarea norului de obiecte intr-un spatiu tridimensional
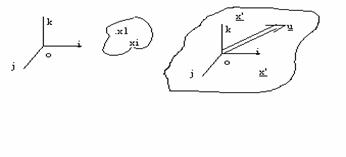
Revenind intr-un spatiu cu d dimensional Rd proiectia vectorului (a caracteristicilor obiectului i) xi pe directia u este matrice [yi] de forma:
[yi]=[u]T[xi]
unde:
[u]T este transpusa matricii componentelor lui u
[xi] este matricea componentelor lui x
Identificand norul de obiecte X cu o matrice [X] de dimensiune d x p ale carei linii corespund caracteristicilor iar coloane obiectelor:
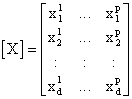
Putem calcula o matrice [Y] a proiectiilor norului de obiecte X pe directia u. Putem scrie ca:
[Y] = [u]T[X] (12)
Imprastierea norului X in directia u este data de dispersia proiectiilor punctelor sale pe u adica de dispersia lui [Y]. Putem deci scrie:
s ([Y]) = s ([u]T[X])=M([u]T[X])2 - (M([u]T[X]))2
dar cum M(X) = 0 , dispersia su X a norului in directia u se scrie:
s uX s ([Y])= M([u]T[X])2 (13)
care da imprastierea gruparii de obiecte in directia u.
Caracteristicile unui obiect pot corespunde la marimi fizice diferite si in consecinta se exprima prin unitati de masura diferite. Pentru calculul distantei ar trebui sa adunam, de exemplu, centimetri si kilograme. Din acest motiv inainte de aplicarea algoritmului de stabilire a apartenentei unui obiect la o clasa este necesar sa efectuam o uniformizare a diferitelor caracteristici. Aceasta uniformizare se poate realiza intr-o normalizare a datelor, astfel incat toate caracteristicile sa aiba aceeasi valoare medie si aceeasi dispersie.
Transformarea
![]() i=1,,d (14)
i=1,,d (14)
este o transformare de normalizare, ce consta dintr-o translatie si o transformare de scala. Prin aceasta transformare a axelor de coordonate, toate caracteristicile au media zero si dispersia unu. In adevar, media si dispersia noii caracteristici i se pot scrie:
M(Xi')=![]() (15a)
(15a)
si
si s (Xi') = M(Xi'-M Xi')2
tinand cont ca M(Xi')=0 rezulta ca :
si = M((Xi')2)
si deci
si =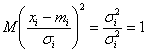 (15b)
(15b)
Normalizarea (14) este utila si in cazul cand caracteristicile au aceeasi unitate de masura. In acest caz normalizarea realizeaza o uniformizare a rolului diferitelor caracteristici, impiedicand anumite caracteristici sa devina dominante in calculul distantei numai datorita faptului ca au valori numerice mari.
Daca valorile unei caracteristici sunt mici, atunci aceste proiectii ale obiectelor pe axa corespunzatoare se reprezinta ca o singura clasa omogena. Dispersia caracteristicii respective fiind mica , prin normalizare valorile numerice ale proiectiilor se maresc. Ca urmare norul proiectiilor nu mai apare omogen ci structurat in clase.
O alternativa la folosirea unei masuri de disimilaritate este considerarea unei masuri a gradului in care obiectele de clasificat sunt asemanatoare.
O masura (coeficient) de similaritate peste X este o functie S:X*X R , care satisface axiomele:
S(x, y)³0, S(x, y)= S(y, x), x , y IX
S(x, x)= S(y, y)> S(x, y) , x , y IX
Daca X este o submultime a spatiului Rd, atunci ca o masura a similaritatii vectorilor (formelor) x si y din X putem considera cosinusul unghiului dintre cei doi vectori. Avem deci masura de similaritate:
S1(x,y)=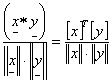 (1)
(1)
unde :
(x .y) - este produsul sacalar a doi vectori, pentru cazul dat avem x1y1+x2y2++xdyd
[x]T - transpusa matricii componentelor formei x
x|| - normala lui x : ![]()
Aceasta masura de similaritate este utila atunci cand multimea X a datelor este formata din clusteri liniari. O distanta poate induce o masura de similaritate. Daca d este o distanta peste X, atunci putem defini distanta normalizata d/dmax, unde:
![]()
Masura de similaritate indusa de distanta d se defineste prin
![]()
Admitem ca toate caracteristicile sunt binare. Fiecare obiect (forma) este reprezentat printr-un vector cu d componente care nu pot fi decat 0 sau 1. Vom pune xi=1 daca obiectul x poseda atributul i si xi=0 in caz contrar. Daca atributul i este prezent simultan la obiectele x si y, atunci avem xi yi =1.
Masura de similaritate (1) poate fi reinterpretata pentru cazul caracteristicilor binare. In acest scop se observa ca numarul de atribute prezente simultan la x si y este
S=![]()
Rezulta
ca ![]() da numarul de atribute pe care le poseda x.
Atunci
da numarul de atribute pe care le poseda x.
Atunci ![]() este media geometrica a numarului de atribute
din
este media geometrica a numarului de atribute
din ![]() si din
si din ![]() si deci S
si deci S![]() data de
data de
![]()
este o masura relativa a numarului de atribute comune. Modificand relatia (1) se pot obtine diverse masuri de similaritate. Se pot obtine astfel:
inlocuind numitorul cu numarul de atribute a unui obiect avem:
![]() (2)
(2)
coeficientul lui Tanimoto
![]()
Aceasta masura este mult utilizata in probleme ridicate de regasirea informatiei, biologie etc.
Se observa ca daca atributul i lipseste simultan din ![]() si
si ![]() atunci (1-xi)(1-yI)=1
si deci
atunci (1-xi)(1-yI)=1
si deci
T=![]() (4)
(4)
este
numarul atributelor ce lipsesc simultan din ![]() si
si ![]() .
.
Analog
u=![]() (5)
(5)
v=![]() (6)
(6)
reprezinta
numarul atributelor prezente in ![]() dar care lipsesc din
dar care lipsesc din ![]() si respectiv
numarul atributelor care sunt prezente in
si respectiv
numarul atributelor care sunt prezente in ![]() dar lipsesc din
dar lipsesc din ![]() .
.
Cu aceste notatii este usor de vazut ca sunt adevarate urmatoarele egalitati
s+u+v+t = d (7a)
s+u =![]() (7b)
(7b)
s+v = ![]() (7c)
(7c)
Tinand cont de considerentele anterioare, semnificatia masurilor de similaritate date mai jos este usor de intuit:
S5(![]() ,
,![]() )=
)=![]() , (Kendal-Sokal) (8)
, (Kendal-Sokal) (8)
S6(![]() ,
,![]() )=
)=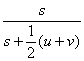 , (Dice) (9)
, (Dice) (9)
S7(![]() ,
,![]() )=
)=![]() , (Sokal-Sneath) (10)
, (Sokal-Sneath) (10)
S8(![]() ,
,![]() )=
)=![]() (Yule) (11)
(Yule) (11)
S9(![]() ,
,![]() )=
)=![]() (Pearson) (12)
(Pearson) (12)
Fie ![]() multimea obiectelor de clasificat. Ne propunem
sa gasim o tehnica de explorare a datelor, care sa ne permita sa descoperim structura
naturala de clasificare, sau structura de clusteri a multimii datelor. Vom
admite ca structura de clasificare a multimii X este data de o partitie
multimea obiectelor de clasificat. Ne propunem
sa gasim o tehnica de explorare a datelor, care sa ne permita sa descoperim structura
naturala de clasificare, sau structura de clusteri a multimii datelor. Vom
admite ca structura de clasificare a multimii X este data de o partitie
![]() a lui X.
a lui X.
Fiecare
element ![]() a partitiei
a partitiei ![]() va corespunde unei clase (nor, cluster) de
obiecte, astfel incat punctele unei clase sa fie mai asemanatoare decat
punctele din clase diferite. Asemanarea obiectelor este data de o masura de
similaritate sau de o masura de disimilaritate. Pe baza unei astfel de masuri
putem construi o functie criteriu. Problema de clasificare se reduce astfel la
problema determinarii partitiei ce realizeaza optimul functiei criteriu
(obiectiv). Pentru a construi o functie obiectiv al carei extrem sa fie
partitia cautata, avem nevoie sa fixam o anumita reprezentare a partitiei.
Aceste reprezentari depind de scopul clasificarii ca si de structura datelor.
Structura se poate postula, bazandu-se pe anumite informatii apriorii, sau poate fi determinata prin aplicarea
unor metode de analiza preliminara a datelor (analiza componentelor principale,
analiza factoriala etc.)
va corespunde unei clase (nor, cluster) de
obiecte, astfel incat punctele unei clase sa fie mai asemanatoare decat
punctele din clase diferite. Asemanarea obiectelor este data de o masura de
similaritate sau de o masura de disimilaritate. Pe baza unei astfel de masuri
putem construi o functie criteriu. Problema de clasificare se reduce astfel la
problema determinarii partitiei ce realizeaza optimul functiei criteriu
(obiectiv). Pentru a construi o functie obiectiv al carei extrem sa fie
partitia cautata, avem nevoie sa fixam o anumita reprezentare a partitiei.
Aceste reprezentari depind de scopul clasificarii ca si de structura datelor.
Structura se poate postula, bazandu-se pe anumite informatii apriorii, sau poate fi determinata prin aplicarea
unor metode de analiza preliminara a datelor (analiza componentelor principale,
analiza factoriala etc.)
Sa admitem faptul ca fiecare clasa ![]() se poate
reprezenta printr-un prototip
se poate
reprezenta printr-un prototip ![]() dintr-un spatiu de reprezentare L.
dintr-un spatiu de reprezentare L.
![]() =
=
constituie
reprezentarea partitiei![]() .
.
Fie D o masura de disimilaritate peste X. Admitem ca pornim de la D se poate construi o disimilaritate intre un obiect din X si un prototip. Acest lucru este intotdeauna posibil cand D este o distanta sau patratul unei distante. Vom nota cu Di aceasta masura de disimilaritate indusa de catre D.
Di este asadar o functie
Di: X![]() z R
z R
si
Di(x, Li)
masoara gradul in care obiectul x difera de prototipul Li
Notam cu
I
: P(X) ![]() qàR
qàR
o functie care masoara gradul de inadecvare al repezentarii unei clase printr-un prototip. Admitem ca masura I(Ai, Li) a inadecvarii clasei Ai prin prototipul Li este data de
I(Ai, Li)
= ![]() Di(x,Li)
Di(x,Li)
dupa care vom considera ca inadecvarea reprezentarii partitiei P prin L este de forma:
J(P, L)
= ![]() I(Ai, Li)
I(Ai, Li)
sau tinand cont de (1):
J(P, L)
= ![]()
unde J reprezinta funtia criterie.
Problema de clasificare se reduce la determinarea partitiei P si a reprezentarii L care minimizeaza aceasta functie criteriu. Deoarece multimea partitiilor cu n clase ale lui X este finita, problema poate fi, teoretic, rezolvata prin considerarea tuturor partitiilor. In realitate acest lucru nu este realizabil decat in situatii foarte particulare. Intr-adevar numarul partitiilor cu n clase ce pot fi construite cu p obiecte este
![]()
Acest numar este foarte mare pentru cele mai multe cazuri practice. De
exemplu, pentru 5 clase si 100 obiecte avem circa ![]() partitii distincte.
partitii distincte.
Cele mai utilizate metode pentru rezolvarea problemei de minimizare a functiei criteriu sunt metodele iterative. Ideea de baza este de a porni de la o partitie initiala, care poate fi aleasa arbritar sau determinata printr-un alt algoritm. Obiectele de clasificat sunt transferate dintr-o clasa in alta, daca o astfel de mutare amelioreaza valoarea functiei criteriu. Procedura se opreste cand nici o schimbare nu mai imbunatateste valoarea functiei criteriu. Procedurile iterative de acest tip asigura atingerea unui optim local. Alegeri diferite ale partitiei initiale vor conduce in final dupa un interval mai mare sau mai mic de timp in general la solutii identice ale problemei de clasificare.
Fie X = multimea obiectelor de clasificat. Admitem ca aceste obiecte reprezinta vectori din spatiul euclidian d-dimensional. Vom considera ca masura de disimilaritate patratul distantei induse de norma, adica
D(x ,y)=![]() (1)
(1)
Presupunem ca multimea X este alcatuita din nori (clusteri) de puncte relativ compacti si bine separati, de forma aproximativ sferica. In aceste conditii un nor se poate reprezenta pritr-un punct, care constituie prototipul clasei respective. Asadar prototipul Li al clasei Ai este un punct din Rd.
Disimilaritatea dintre un punct x din X si prototipul Li se poate interpreta ca fiind eroarea comisa atunci cand punctul x se aproximeaza prin prototipul clasei Ai. Aceasta disimilaritate se poate scrie
D(x ,Li)=![]() (2)
(2)
Functia criteriu considerata va fi:
J(P, L)
=![]() (3a)
(3a)
de unde
J(P, L)
=![]() (3b)
(3b)
Pentru
a determina minimul functiei criteriu, aceasta se va exprima intr-o forma usor
modificata. Fie IAi functia caracteristica a multimii Ai.
Folosind notatia:![]()
Aij = IAi(xj) =![]() (4)
(4)
Sa presupunem de exemplu ca avem un numar de 6 obiecte si ca partitionarea acestora initiala este 3. Atunci Aij se va putea construi astfel:
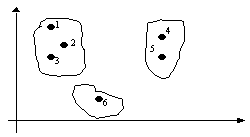
Partitia
|
Obiect | |||
In aceste conditii functia criteriu este:
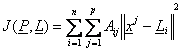 (5)
(5)
Tinand cont de faptul ca intr-un spatiu euclidian produsul scalar a doi vectori este
![]()
functia criteriu apare sub forma
![]()
Pentru
ca ![]() sa fie un minim pentru functia
sa fie un minim pentru functia ![]() este necesar sa avem:
este necesar sa avem:
![]() (7)
(7)
de unde rezulta ca:
![]()
respectiv:
![]()
de unde obtinem:
 (10)
(10)
Se
observa ca numitorul reprezinta numarul de elemente din clasa ![]() . Notand cu
. Notand cu
![]() numarul de elemente din clasa Ai (11)
numarul de elemente din clasa Ai (11)
expresia prototipului Li se va mai scrie
![]() (12)
(12)
Observam ca prototipul L i este media sau centrul de greutate al clasei A i.
Reprezentarea
L i
unde L i este dat de (10), induce o noua partitie. Aceasta partitie se obtine folosind regula celui mai apropiat vecin. Un obiect (punct) xj este atasat clasei de centrul careia este cel mai apropiat. Avem deci urmatoarea regula de decizie
![]()
![]() (13)
(13)
Din punctul de vedere al programarii algoritmului, este mai util regula (13) sa se exprime sub forma
![]()
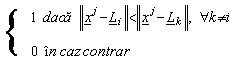
Algoritmul n-medii consta in aplicarea iterativa a formulelor (10), (14) sau (12), (13), plecand de la o partitie initiala a lui X. Aceasta partitie initiala se poate alege arbitrar, se poate stabili folosind anumite informatii asupra datelor sau poate constitui rezultatul aplicarii unui alt algoritm de clasificare.
Algoritmul n-medii consta in executarea urmatorilor pasi:
P1. Se alege o partitie initiala p0= a lui X.
P2. Se calculeaza prototipurile acestei partitii cu formula :

P3. Se calculeaza noua partitie dupa regula
x A i daca ![]()
P4. Daca noua partitie coincide cu precedenta, atunci STOP. In caz contrar se merge la P2.
Observatii:
A) In loc de a alege o partitie initiala putem porni de la o alegere arbitrara a n centrii, care pot fi n puncte din multimea X a datelor.
B) Rezultatele algoritmului n-medii depind de numarul de clase considerate, de alegerea initiala a partitiei sau a centrilor si de propietatile geometrice ale datelor. Cand datele contin grupari caracteristice, relativ indepartate unele de altele, deci sunt constituite din clusteri compacti si bine separati, rezulatele algoritmului sunt bune. Determinarea numarului optim de clusteri prezenti in multimea datelor constituie asa numita problema a validitatii clusterilor. Aceasta problema nu poate fi rezolvata in cadrul acestui algoritm. Daca avem unele informatii despre date, putem ca prin experimentari succesive sa determinam valoarea care da cea mai buna concordanta cu datele initiale.
C) O alta problema dificila apare cand datele contin clase ce prezinta diferente mari ale numarului de puncte. Sa consideram cazul cand datele constau din doi clusteri inegali ca populatie si extindere. Este posibil ca unele puncte aflate la periferia clusterului mare sa fie mai apropiate de centrul clusterului mic. Functia criteriu considerata va favoriza o partitie ce despica clusterul mare, fata de una ce mentine integritatea acestuia. Daca se considera n=2, atunci clusterul mai mic va capta unele din punctele periferice ale clusterului mare. Acest efect 'pseudo-gravitational' reprezinta o perturbatie pentru procesul de clasificare. Este o dificulatate majora care se poate rezolva facand ca distanta de la un obiect la prototipul unei clase sa depinda de dimensiunea clasei respective. Considerarea unei astfel de distante adaptive presupune in general ca algoritmul sa fie aplicat de doua ori.
D) Alte dificultati sunt legate de existenta punctelor izolate (considerate zgomote) si a podurilor intre clustere. De altfel aceste dificultati apar si in alte tehnici de clasificare.
Algoritmul ISODATA (Iterativ Self-Organizing Data Analyst Techniques) este in esenta similar cu algoritmul n-medii. Aceasta asemanare a facut ca algoritmul n-medii sa fie deseori prezentat sub numele de ISODATA. Asemanarea consta in modul iterativ de calcul a centrilor. Deosebirea este data de natura euristica a algoritmului ISODATA. Algoritmul reprezinta un bun exemplu relativ la avantajele si inconvenientele unor astfel de metode care necesita definirea unor parametrii ce trebuie ajustati prin incercari succesive.
Mai intai este necesar sa se specifice k centri de clase. Acesti centri, al caror numar nu este neaparat egal cu numarul claselor dorite, pot fi alesi dintre punctele de clasificat. Fie m1,,mk alegerea initiala arbitrara a acestor centri.
Algoritmul ISODATA consta in parcurgerea urmatorilor pasi:
P1. Se specifica valorile urmatorilor parametri:
n = numarul de clase dorite;
qp = numarul minim de elemente dintr-o clasa;
qs = parametrul de dispersie standard;
qc = distanta maxima pentru fuzionare;
L = numarul maxim de perechi de centre ce pot fuziona la un moment dat;
I = numarul maxim de iteratii permise.
P2. Se distribuie cele p perechi din X in clasele determinate de centri, dupa regula:
![]()
P3. Se suprima clasele avand mai putin de ![]() elemente si se repartizeaza obiectele in
celelalte clase. Se micsoreaza k.
elemente si se repartizeaza obiectele in
celelalte clase. Se micsoreaza k.
P4. Se recalculeaza centrii claselor dupa formula
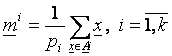
P5. Se calculeaza diametrul mediu al fiecarei clase
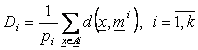
P6. Se calculeaza distanta medie la care se afla obiectele fata de centrii claselor
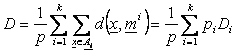
P7. 1)
Daca aceasta este ultima iteratie atunci se pune ![]() si se merge la P11
si se merge la P11
2)
Daca ![]() se merge la P8
se merge la P8
3)
Daca numarul iteratiei este par sau daca ![]() se merge la P11
se merge la P11
P8. Se calculeaza dispersia clasei ![]()
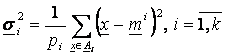
Componenta ![]() a lui
a lui ![]() reprezinta dispersia datelor in directia j.
reprezinta dispersia datelor in directia j.
P9. Pentru fiecare clasa se determina componenta maxima a dispersiei
![]()
P10. Se considera succesiv toate clasele. Daca
exista o clasa ![]() astfel incat
astfel incat
![]()
si![]()
![]()
sau
![]()
atunci se despica clasa Ai in doua clase si se claculeaza centrii acestora
![]() si
si ![]()
se
sterge ![]() si se pune
si se pune ![]() . Centrul
. Centrul ![]() se obtine
adaugand la componenta
se obtine
adaugand la componenta ![]() (care
corespunde componentei maxime ale lui
(care
corespunde componentei maxime ale lui ![]() ) o
cantitate
) o
cantitate ![]() (unde
(unde ![]() ). Centrul
). Centrul ![]() se obtine
scazand aceasta cantitate din
se obtine
scazand aceasta cantitate din ![]() . Parametrul
trebuie astfel ales incat diferenta distantelor de la orice punct arbitrar la
noii centri sa fie sesizabila ( mai mare decat un
. Parametrul
trebuie astfel ales incat diferenta distantelor de la orice punct arbitrar la
noii centri sa fie sesizabila ( mai mare decat un ![]() convenabil ales), dar sa nu schimbe in mod
apreciabil intreaga configuratie a claselor.
convenabil ales), dar sa nu schimbe in mod
apreciabil intreaga configuratie a claselor.
Daca s-a produs despicarea vreunei clase la acest pas se merge la P2. In caz contrar se va continua.
P11. Se calculeaza toate distantele intre centri claselor
![]()
P12. Se compara distantele dij cu parametrul ![]() . Se
aranjeaza primele L distante mai mici
decat
. Se
aranjeaza primele L distante mai mici
decat ![]() in ordine crescatoare.
in ordine crescatoare.
P13. Pornind de la perechea de clase ![]() avand distanta centrilor cea mai mica se
modifica centrii dupa urmatoarea regula: Daca atat pentru
avand distanta centrilor cea mai mica se
modifica centrii dupa urmatoarea regula: Daca atat pentru ![]() cat si pentru
cat si pentru ![]() centrul nu a fost modificat, se inlocuiesc
centrii
centrul nu a fost modificat, se inlocuiesc
centrii ![]() prin centrul
prin centrul
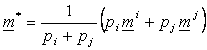 .
.
Se
sterg ![]() si se pune
si se pune ![]() . Daca fie
. Daca fie ![]() fie
fie ![]() au centrul modificat atunci perechea (i, j) nu
e luata in considerare si se trece la urmatoarea pereche.
au centrul modificat atunci perechea (i, j) nu
e luata in considerare si se trece la urmatoarea pereche.
P14. Daca aceasta este ultima iteratie sau daca pozitia si numarul centrilor coincid cu cele de la iteratia precedenta STOP. In caz contrar se merge la P2 ( sau P1 daca se modifica datele intiale).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1375
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved