| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
SESIUNEA DE REFERATE STIINTIFICE
EDITIA A VII-A
25-APRILIE-2009
REFERAT
PROBLEME DE MINIM SAU DE MAXIM
Rezumat
Numeroase probleme de matematica,fizica,astrofizica ,precum si cele ce prezinta un interes deosebit in practica ,opereaza cu marimi variabile pentru care in anumite conditii se cere sa se afle cea mai mica sau cea mai mare valoare.
Problemele de minim sau maxim sunt printre cele mai frumoase si interesante probleme abordate de matematica.O parte din aceastea pot fi solutionate elementar ,dar cele mai multe necesita cunostinte solide din teoria optimizarii functiilor.
Cu ajutorul minimului sau maximului trinomului de gradul al doilea am determinat
aria unui paralelogram ABCD pe laturile
caruia au fost luate punctele M,N,P,Q la egala distanta
fata de A,B,C,respectiv D sau am gasit doua numere
reale a caror diferenta
se cunoaste si al caror produs este minim.In continuare am
determinat punctele de extrem local ale unei functii si am gasit un punct M astfel incat
pentru n puncte M1,M2,.,Mn, suma![]() sa fie minima.
sa fie minima.
La punctul 2 am rezolvat diverse probleme in carea am determinat maximul produsului a doua numere reale pentru suma constanta , de exemplu maximul functiei reale f(x)=(24 - 6x + x)(4 + 6x - x) si demonstrarea ca dintre toate dreptunghiurile de acelasi perimetru,patratul are aria maxima.
Minimul
sumei pentru produs constant ne ajuta sa determinam minimul
functiei definite pe![]() .
.
O alta aplicatie poate fi inegalitatea dintre media aritmetica,media geometrica si media armonica .
Ultimul tip propus in acest material se refera la minimele si maximele trigonometrice si geometrice in care am prezentat unele dintre cele mai interesante probleme :
Dintre toate triunghiurile ce se pot circumscrie unui cerc de raza r , sa se determine triunghiul de arie minima,
Dintre toate patrulaterele convexe ce se pot forma cu patru segmente date , cel inscriptibil (daca exista) are aria maxima
si altele.
Probleme de minim sau maxim
Numeroase probleme de matematica,fizica,astrofizica ,precum si cele ce prezinta un interes deosebit in practica ,opereaza cu marimi variabile pentru care in anumite conditii se cere sa se afle cea mai mica sau cea mai mare valoare.
Problemele de minim sau maxim sunt printre cele mai frumoase si interesante probleme abordate de matematica.O parte din aceastea pot fi solutionate elementar ,dar cele mai multe necesita cunostinte solide din teoria optimizarii functiilor.
1.Minimul sau maximul trinomului de gradul al doilea:
Fie trinomul real![]() care are forma canonica
care are forma canonica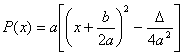 ,unde
,unde![]() este discriminant,functia x→P(x) isi atinge
valorile extreme odata cu functia
este discriminant,functia x→P(x) isi atinge
valorile extreme odata cu functia ![]() .
.
Astfel ![]() daca a>0 si
daca a>0 si ![]() ,daca a<0.
,daca a<0.
![]() se numeste varful parabolei
asociate functiei de gradul al doilea
se numeste varful parabolei
asociate functiei de gradul al doilea ![]() :R→R,
:R→R, ![]() .
.
Exemple:
1. Pe laturile dreptunghiului
Sa se afle aria paralelogramului MNPQ cand x variaza.
Solutie:
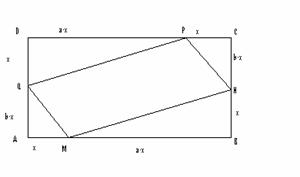

![]() a>0,deci
a>0,deci ![]() .
.
![]() .
.
![]() Pentru
Pentru![]() .
.
![]()
![]()
2. Diferenta a doua numere reale este α .Care sunt aceste numere daca produsul lor este minim?
Solutie:
Fie x si ![]() numerele
=>P(x)=x(x+α)
=x+x α ,este minim
pentru
numerele
=>P(x)=x(x+α)
=x+x α ,este minim
pentru ![]()
Deci
numerele sunt ![]() adica
adica ![]()
3. Sa se afle multimea
valorilor functiei![]() si sa se precizeze punctele de extrem local ale
lui
si sa se precizeze punctele de extrem local ale
lui![]() .
.
Solutie:
f(x)=y,![]()
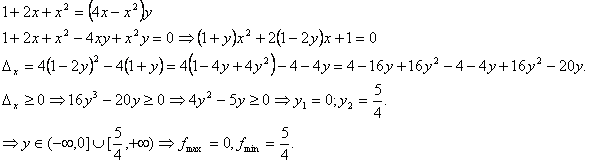
2.
![]() puncte
de maxim local ; x
puncte
de maxim local ; x ![]()
Observatie:
Metoda
poate fi folosita pentru toate functiile de forma ![]()
4. Pe o axa data consideram
n puncte fixe![]() de abcise
de abcise ![]()
Determinati
pe aceasta axa un punct M de
abcisa x astfel ca suma![]() sa fie minima.
sa fie minima.
Solutie:
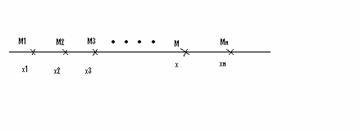
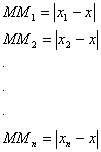
Atunci ![]()
![]() minima
pentru
minima
pentru 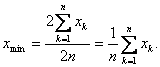
2. Maximul produsului pentru suma constanta
Fie![]() variabile pentru care
variabile pentru care![]() constant.Atunci
constant.Atunci ![]() sau
sau![]() (variabil).
(variabil).
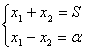
3.
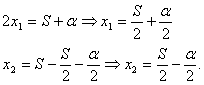
![]() creste(descreste) cand
creste(descreste) cand ![]() descreste(creste).
descreste(creste).
P este
maxim <=> α=0 ,adica![]() , deci oricare ar fi x ≠ y ,
, deci oricare ar fi x ≠ y , ![]() ∙
∙ ![]() ≥ x ∙ y .
≥ x ∙ y .
Exemple :
Dintre toate dreptunghiurile de acelasi perimetru P , patratul are aria maxima.
Solutie :
Fie L lungimea
l latimea dreptungiului
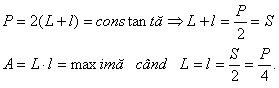
Observatie :
Analog,dintre toate paralelipipedele cu suma lungimilor tuturor
muchiilor
Doua fete concentrate![]() si
si![]() ale caror
directii fac un unghi de 60۫ au variabile cu suma de 2N. Sa
se gaseasca aceste forte astfel incat rezultanta lor sa
aiba marimea minima.
ale caror
directii fac un unghi de 60۫ au variabile cu suma de 2N. Sa
se gaseasca aceste forte astfel incat rezultanta lor sa
aiba marimea minima. 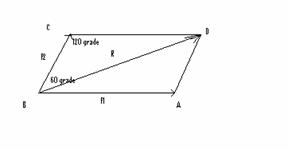
4.
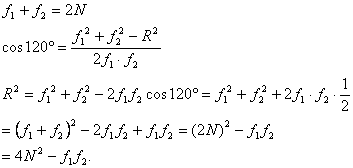
![]() cand
cand ![]() maxim
maxim![]()
3. Sa se afle maximul functiei reale f(x (24 - 6x + x)(4 + 6x - x)
Solutie:
Fie a = 24 - 6x + x
b = 4 + 6x - x
Observam ca a + b = 28 =
![]() se realizeaza
daca
se realizeaza
daca ![]()
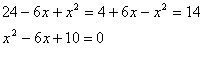 au solutii
complexe
au solutii
complexe
Sa se determine maximul functiei f(x)=(3x - 1)(4 - 2x)(1 - 2x) ,
x![]()
![]()
Solutie:
f continua si derivabila pe (![]()
=>f(x)=![]()
![]()
f '(x) = 0![]()
![]()
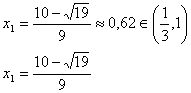
punct de maxim global al lui f .
5.
max f(x) =
f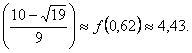
Sa se determine cilindrul de volum maxim care se poate inscrie intr-un con dat.
Solutie:
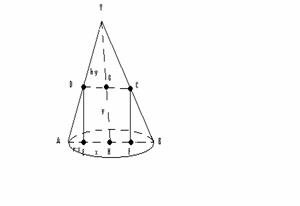
![]()

Miniumul sumei pentru produs constant
Fie n
nr. reale pozitive![]() pentru care
pentru care![]() constant ; suma S=
constant ; suma S=![]() este minima numai cand
este minima numai cand ![]()
Daca
![]() ,atunci S =
,atunci S =![]()
P.p
ca exista o valoare min S = So <![]() ,valoarea
,valoarea![]() fiind
atinsa de exemplu pentru
fiind
atinsa de exemplu pentru ![]() fals pentru ca P = const.
fals pentru ca P = const.
Analog putem demonstra ca min S nu poate fi mai mare decat ![]() =>S =
=>S =![]() atinsa pentru
atinsa pentru![]()
6.
Exemple
Dintre toate dreptunghiurile de arie alba patratul are perimetrul minim
Solutie
![]() minima
minima ![]() L + l.
L + l.
Observatie : Dintre toate paralepipedele de volum dat cubul are suma lungimilor tuturor muchiilor minima.
Sa se afle minimul functiei definite pe![]() .
.
Solutie:
![]() minima atunci
cand
minima atunci
cand![]()
![]()
4. Inegalitati dintre media aritmetica,media geometrica si media armonica
Fie![]()
Atunci: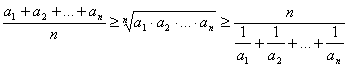 egalitatile
avand loc
egalitatile
avand loc ![]()
Daca
notam ![]()
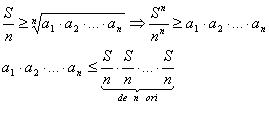
Daca notam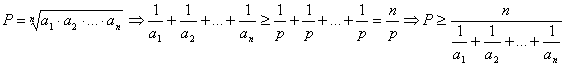
7.

Exemplu
Sa se determine conditiile in care se realizeaza minimul functiei f : ( 0 , ∞ ) → R
f(x)
=![]() .
.
Solutie:
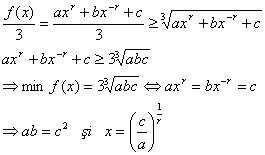
5. Minim si maxim trigonometrice si geometrice
1) Fie![]() [0, π]. Daca
[0, π]. Daca![]() = S = const ≤ π.
= S = const ≤ π.
![]() este maxim numai cand unghiurile
este maxim numai cand unghiurile ![]() .
.
Solutie:

Observatie : Propietatea se poate generalize.
8.
Daca![]() este maxim numai
cand
este maxim numai
cand ![]() (daca acest
lucru este posibil).
(daca acest
lucru este posibil).
Se da E = sinα + sinβ + sinγ , unde α β γ sunt masurile in radiani ale unghiurilor unui triunghi oarecare.Sa se determine triunghiul pentru care E are valoarea maxima .
Solutie :
![]()
E = sinα + sinβ + sin[π
α β)] = 2sin![]() cos
cos![]() + sin (α β
+ sin (α β
= 2sin![]() cos
cos![]() + 2sin
+ 2sin![]() cos
cos![]() =
=
= 2sin![]() (cos
(cos![]() + cos
+ cos![]() ) =
) =
= 2sin![]() 2cos
2cos![]() cos
cos![]() =
=
= 4sin![]() cos
cos![]() cos
cos![]() =
=
= 4sin![]() cos
cos![]() cos
cos![]() =
=
= 4cos![]() cos
cos![]() cos γ
cos γ![]()
= 4sin![]() sin
sin![]() sin
sin![]()

atins numai pentru triunghi echilateral .
Dintre toate triunghiurile ce se pot circumscrie unui cerc de raza r , sa se determine triunghiul de arie minima.
Solutie:
9.
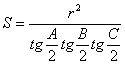
S este
minima cand tg![]() tg
tg![]() tg
tg![]() este minima
este minima ![]()
![]() ,deoarece
,deoarece ![]()
![]() .
.
Dintre toate patrulaterele convexe ce se pot forma cu patru segmente date , cel inscriptibil (daca exista) are aria maxima.
Solutie:
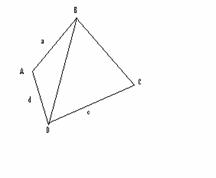
Daca AB=a,BC=b,CD=c,DA=d

10.
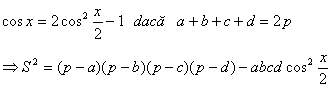
Deci S![]() este maxim
este maxim![]()
![]() ,adica ABCD
patrulater inscriptibil
,adica ABCD
patrulater inscriptibil
![]() .
.
11.
Bibliografie
Dumitru Busneag,Jian Maftei : Teme pentru cercurile si concursurile de matematica ale elevilor,Suisul Romanesc,Craiova 1983
T. Albu,I. Ionescu : Principiul includerii si al excluderii(G.M. nr.6 1969)
Seria Gazeta Matematica.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 8544
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved