Scrigroup - Documente si articole

     

 
HomeDocumenteUploadResurseAlte limbi doc
 
AstronomieBiofizicaBiologieBotanicaCartiChimieCopii
Educatie civicaFabule ghicitoriFizicaGramaticaJocLiteratura romanaLogica
MatematicaPoeziiPsihologie psihiatrieSociologie


Principiul Inductiei Matematice

Matematica



+ Font mai mare | - Font mai mic



Principiul Inductiei Matematice.

Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural.



Metoda inductiei matematice consta in urmatoarele:

O propozitie (afirmatie) oarecare P(n), ce depinde de un numar natural n, este adevarata pentru orice n natural, daca:

  1. P(1) este o propozitie (afirmatie) adevarata;
  2. P(n) ramane o propozitie (afirmatie) adevarata, cand n se majoreaza cu o unitate, adica P(n + 1) este adevarata.

Asadar, metoda inductiei presupune doua etape:

  1. Etapa de verificare:   se verifica daca propozitia P(1) este adevarata;
  2. Etapa de demonstrare: se presupune ca propozitia P(n) este adevarata si se demonstreaza justetea afirmatiei P(n + 1) (n a fost majorat cu o unutate).

Nota In unele cazuri metoda inductiei matematice se utilizeaza in urmatoarea forma:

Fie m un numar natural, m > 1 si P(n) o propozitie ce depinde de n, n m.

Daca

  1. P(m) este adevarata;
  2. P(n) fiind o propozitie justa implica P(n + 1) adevarata pentru n m, atunci P(n) este o propozitie adevarata pentru orice numar natural n m.

In continuare sa ilustram metoda inductiei matematice prin exemple.

Exemplul Sa se demonstreze urmatoarele egalitati

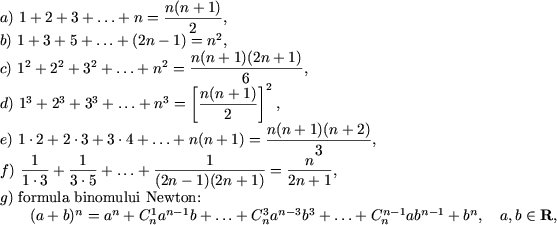
unde n I N.

Rezolvare a) Pentru n = 1 egalitatea devine 1=1, prin urmare P(1) este adevarata. Presupunem ca egalitatea din enunt este adevarata, adica are loc egalitatea

,

si urmeaza sa verificam daca P(n + 1), adica

este justa. Cum (se tine seama de egalitatea din enunt)

se obtine

adica P(n + 1) este afirmatie justa.

Asadar, conform principiului inductiei matematice egalitatea din enunt este justa pentru orice n natural.

Nota Mentionam ca acest exemplu poate fi rezolvat si fara utilizarea inductiei matematice. Intr-adevar, suma 1 + 2 + 3 + + n reprezinta suma primilor n termeni ai progresiei aritmetice cu primul termen a1 = 1 si ratia d = 1. In baza formulei cunoscute se obtine

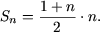
b) Pentru n = 1 egalitatea devine 21 - 1 = 12 sau 1=1, astfel P(1) este justa. Presupunem justa egalitatea

1 + 3 + 5 + + (2n - 1) = n2

si urmeaza sa verificam daca are loc P(n + 1):

1 + 3 + 5 + + (2n - 1) + (2(n + 1) - 1) = (n + 1)2

sau

1 + 3 + 5 + + (2n - 1) + (2n + 1) = (n + 1)2.

Se tine seama de egalitatea din enunt si se obtine

1 + 3 + 5 + + (2n - 1) + (2n + 1) = n2 + (2n + 1) = (n + 1)2.

Asadar P(n + 1) este adevarata si, prin urmare, egalitatea din enunt este adevarata.

Nota Similar exemplului precedent, se rezolva si fara a aplica metoda inductiei matematice.

c) Pentru n = 1 egalitatea este justa 1=1. Se presupune justa egalitatea

si se arata ca

adica P(n) adevarata implica P(n + 1) adevarata. In adevar

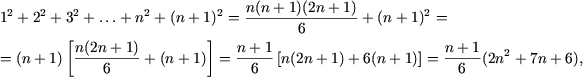
si cum 2n2 + 7n + 6 = (2n + 3)(n + 2) se obtine

si, prin urmare, egalitatea este adevarata.

d) Pentru n = 1 egalitatea este justa: 1=1. Se presupune ca are loc egalitatea

si se arata ca are loc egalitatea

In adevar, tinand seama de ipoteza

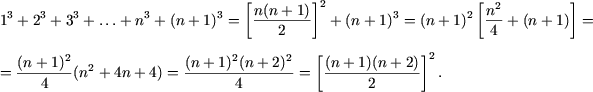
e) Propozitia P(1) este justa 2=2. Se presupune ca egalitatea

este adevarata si se arata ca ea implica egalitatea

In adevar

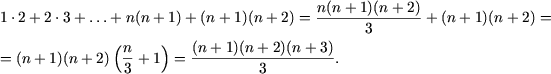
Asadar, egalitatea enuntata este justa pentru orice n natural.

f) P(1) este adevarata: 1/3 = 1/3. Se presupune ca are loc P(n):

si se arata ca aceasta egalitate implica egalitatea

In adevar, tinand seama de justetea afirmatiei P(n), se obtine

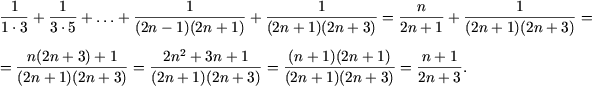
Prin urmare, egalitatea este demonstrata.

g) Pentru n = 1 egalitatea devine a + b = b + a, si deci este adevarata.

Fie formula binomului Newton este justa pentru n = k, adica

Atunci

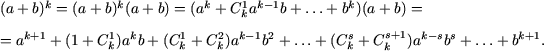
Tinand seama de egalitatea se obtine

Exemplul Sa se demonstreze inegalitatile

a) inegalitatea Bernuolli: (1 + a)n 1 + na a > -1,     n I N.

b) x1 + x2 + + xn n,   daca   x1x2 xn = 1   si   xi > 0,   .

c) inegalitatea Cauchy relativa la media aritmetica si geometrica
      unde   xi > 0, , n

d) sin2na + cos2na 1,     n I N.

e)

f) 2n > n3,     n I N, n

Rezolvare a) Pentru n = 1 inegalitatea este adevarata

a a

Se presupune ca are loc inegalitatea enuntata

a)n 1 + na

si se arata, ca in asa ipoteza are loc si

a)n 1 + (n + 1)a

In adevar, cum a > -1 implica a + 1 > 0, multiplicand ambii membri ai inegalitatii (1) cu (a + 1) se obtine

a)n a (1 + na a

sau

a)n 1 + (n + 1)a + na

Cum na 0, rezulta

a)n 1 + (n + 1)a + na 1 + (n + 1)a

Asadar P(n) adevarata implica P(n + 1) adevarata, prin urmare, conform principiului inductiei matematice inegalitatea Bernoulli este adevarata.

b) Pentru n = 1, se obtine x1 = 1, si, prin urmare x1 1, adica P(1) este o afirmatie justa. Se presupune ca P(n) este adevarata, adica, x1,x2,,xn sunt n numere pozitive, prodususul carora este egal cu unu, x1x2xn = 1, si x1 + x2 + + xn n.

Sa aratam, ca aceasta ipoteza implica justetea urmatoarei afirmatii: daca x1,x2,,xn,xn+1 sunt (n + 1) numere pozitive cu x1x2xnxn+1 = 1  atunci  x1 + x2 + + xn + xn + 1 n + 1.

Se disting urmatoarele doua cazuri:

1) x1 = x2 = = xn = xn+1 = 1 si atunci suma lor este (n + 1), inegalitatea fiind justa,

2) cel putin un numar este diferit de unu, fie mai mare ca unu. Atunci, dat fiind x1x2 xnxn + 1 = 1, rezulta ca exista cel putin inca un numar diferit de unu, mai exact, mai mic ca unu. Fie xn + 1 > 1 si xn < 1. Consideram n numere pozitive

x ,x2,,xn-1,(xnxn+1).

Produsul lor este egal cu unu, iar conform ipotezei

x + x2 + + xn-1 + xnxn + 1 n.

Ultima inegalitate se scrie astfel

x + x2 + + xn-1 + xnxn+1 + xn + xn+1 n + xn + xn+1

sau

x + x2 + + xn-1 + xn + xn+1 n + xn + xn+1 - xnxn+1.

Cum

n + xn + xn+1 - xnxn+1 = n + 1 + xn+1(1 - xn) - 1 + xn =
= n + 1 + xn+1(1 - xn) - (1 - xn) = n + 1 + (1 - xn xn+1 - 1) n + 1

deoarece

(1 - xn)(xn+1 - 1) > 0,

rezulta

x + x2 + + xn + xn+1 n+1,

adica P(n) adevarata implica P(n + 1) adevarata. Inegalitatea este demonstrata.

Nota Se observa, ca semnul egalitatii are loc daca si numai daca x1 = x2 = = xn = 1.

c) Fie x1,x2,,xn numere pozitive arbitrare. Se considera n numere

Cum aceste numere sunt pozitive si produsul lor este egal cu unu

conform inegalitatii b) demonstrate anterior rezulta

de unde rezulta

Nota Semnul egalitatii are loc daca si numai daca x1 = x2 = = xn.

d) P(1) este o afirmatie justa: sin2a + cos2a = 1. Se presupune ca P(n) este o afirmatie adevarata:

sin2na + cos2na

si se arata ca P(n + 1) are loc. In adevar

sin2(n a + cos2(n + 1)a = sin2nasin2a + cos2nacos2a < sin2na + cos2na

(se tine seama ca daca sin2a 1 atunci cos2a < 1 si reciproc daca cos2a 1 atunci sin2a < 1). Asadar, pentru orice n I N    sin2na + cos2n 1 si semnul egalitatii se atinge doar pentru n = 1.

e) Pentru n = 1 afirmatia este justa:     1 < 3/2.

Se presupune ca si urmeaza de a demonstra ca

Cum

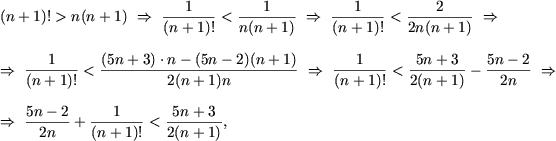
se tine seama de P(n) si se obtine

f) Se tine seama de nota 1 si se verifica P(10): 210 > 103, 1024 > 1000, asadar pentru n = 10 inegalitatea este justa. Se presupune ca 2n > n3    (n > 10) si trebuie de demonstrat P(n + 1), adica 2n+1 > (n + 1)3.

Cum pentru n > 10 avem sau rezulta

2n3 > n3 + 3n2 + 3n + 1   sau   n3 > 3n2 + 3n + 1.

Se tine seama de ipoteza (2n > n3) si se obtine

2n+1 = 2n2 = 2n + 2n > n3 + n3 > n3 + 3n2 + 3n + 1 = (n + 1)3.

Asadar conform principiului inductiei pentru orice n I N,     n 10 avem 2n > n3.

Exemplul Sa se demonstreze ca pentru orice n I N

a) n(2n2 - 3n + 1)   se divide cu 6,

b) 62n-2 + 3n+1 + 3n-1   se divide cu 11.

Rezolvare a) P(1) este o propozitie adevarata ( 0 se divide cu 6). Fie P(n) are loc, adica n(2n2 - 3n + 1) = n(n - 1)(2n - 1) se divide cu 6. Se arata, ca are loc P(n + 1) adica (n + 1)n(2n + 1) se divide cu 6. In adevar, cum

n(n + 1)(2n + 1) = n(n - 1 + 2)(2n - 1 + 2) = (n(n - 1) + 2n)(2n - 1 + 2) =

= n(n - 1)(2n - 1) + 2n(n - 1) + 2n(2n + 1) = n(n - 1)(2n - 1) + 2n3n =

= n(n - 1)(2n - 1) + 6n2

si cum atat n(n - 1)(2n - 1) cat si 6n2 se divid cu 6, rezulta ca si suma lor, adica n(n + 1)(2n + 1) se divide cu 6.

Asadar P(n + 1) este o afirmatie justa, si n(2n2 - 3n + 1) se divide cu 6 pentru orice n I N.

b) Se verifica P(1): 60 + 32 + 30 = 11, prin urmare P(1) este justa. Urmeaza sa se arate, ca daca 62n-2 + 3n+1 + 3n-1 se divide cu 11 (P(n)), atunci 62n + 3n+2 + 3n de asemenea se divide cu 11 (P(n + 1)). In adevar, cum

62n + 3n+2 + 3n = 62n-2+2 + 3n+1+1 + 3n-1+1 =

= 6262n-2 + 33n+1 + 33n-1 = 3(62n-2 + 3n+1 + 3n-1) + 3362n-2

si atat 62n-2 + 3n+1 + 3n-1, cat si 3362n-2 se divid cu 11, rezulta ca si suma lor, adica 62n + 3n+2 + 3n se divide cu 11.

Inductia in geometrie.

Exemplul Sa se calculeze latura a unui poligon regulat cu 2n laturi inscris intr-o circumferinta de raza R.

Rezolvare Pentru n = 2 poligonul regulat cu 22 laturi reprezinta un patrat, si in acest caz a4 = R.

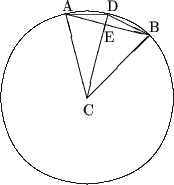
Fie si sa determinam . Daca AB = a , atunci AE = a /2; BD = a . Din triunghiul DEB, conform teoremei Pitagora

La randul sau DE = R-EC si

Asadar si deci,

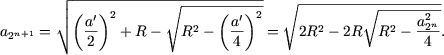
Astfel s-a obtinut o formula de trecere de la n la n + 1. In cazuri particulare:

Natural apare ipoteza

Cum a fost arata anterior, pentru n = 1 aceasta formula este adevarata.

Fie (2) adevarata pentru n = k. Sa calculam . Conform formulei de trecere se obtine

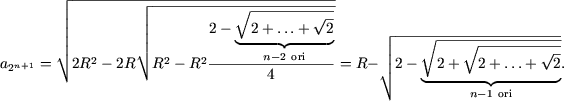
Nota Din (2) rezulta ca lungimea circumferintei este egala cu

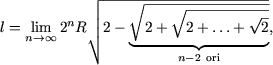
si cum l = 2pR, se obtine

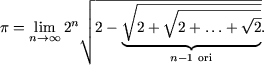
Exercitii pentru autoevaluare

I. Sa se demonstreze egalitatile:

II. Sa se demonstreze inegalitatile

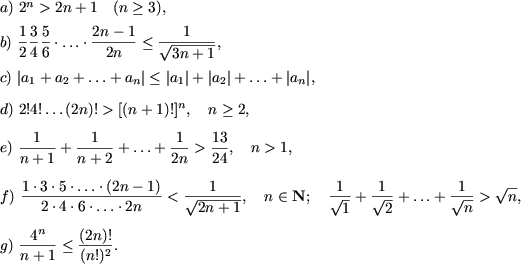
III. Sa se demonstreze, ca pentru orice numar natural, numarul an se divide cu b

a) an = 5n+3 + 113n+1,    b = 17,

b) an = 11n+2 + 122n+1,    b = 133,

c) an = 2n3 + 3n2 + 7n,    b = 6,

d) an = 10n + 18n - 28,    b = 27,

e) an = n5 - n,    b = 30.

IV. Sa se arate, ca 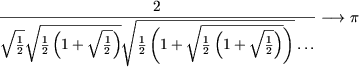  (Formula lui Viete).

V. Sa se calculeze razele rn, Rn a circumferintelor inscrise si circumscrise poligonului regulat cu 2n laturi de perimetru p.

VI. Sa se determine in cate triughiuri poate fi divizat un poligon cu n laturi de diagonalele sale neconcurente.

VII. Fie date n patrate arbitrare. Sa se arate ca aceste patrate pot fi taiate in asa mod incat din partile obtinute se poate de format un patrat.


Politica de confidentialitate | Termeni si conditii de utilizare



DISTRIBUIE DOCUMENTUL

Comentarii


Vizualizari: 2364
Importanta: rank

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved