analiza riscului in procesul de alocare a capitalului

riscul in analiza financiara

Oricare investitor, fie el autohton sau strain, isi pune intrebarea ce se va intampla cu banii pe care ii cheltuieste sub forma de investitii. Desigur, el afecteaza in acest scop o parte din venituri in speranta obtinerii unei cresteri a productiei, realizarii de profituri sporite intr-un viitor mai apropiat sau mai indepartat, dupa intrarea in functiune a obiectivului de investitie. Cu toata previziunea efectuata, investitiile sunt riscante, deoarece profitul depinde de un viitor nesigur. Deci, in activitatea firmei isi fac loc incertitudinea si riscul.

Riscul unui activ se defineste prin variabilitatea probabila a rentabilitatii viitoare. Riscul este legat de probabilitatea de a avea o rentabilitate mai mica decat cea asteptata - cu cat este mai mare sansa unei rentabilitati mici sau negative, cu atat mai riscanta este investitia. Pentru a defini riscul mai precis, putem folosi concepte statistice.

1.1.distributii de probabilitate

Orice decizie de investitii si de aceea, aproape orice decizie de afaceri, necesita o previziune a unor elemente viitoare. In deciziile de alocare a capitalului previziunile cheie sunt legate de fluxurile de numerar anuale ale proiectului. De multe ori, aceasta previziune este facuta sub forma unui numar, adica o estimatie punctuala, denumita frecvent estimatia cea mai probabila. Dar se pune intrebarea, cat de buna este aceasta estimatie punctuala, cata incredere putem avea in rentabilitatea previzionata: este foarte certa, dimpotriva este foarte incerta, sau este undeva la mijloc? Acest grad de incertitudine poate fi definit si masurat prin distributia de probabilitate a predictiei, adica asocierea estimarii probabilitatii cu fiecare rezultat posibil. In forma cea mai simpla, distributia de probabilitate poate consta doar din cateva rezultate potentiale. De exemplu, in previziunea fluxurilor de numerar, putem face o estimatie optimista, una pesimista si cea mai probabila estimatie. Alternativ, putem face o estimatie maxima, una minima si cea mai buna aproximatie. Ne putem astepta, de exemplu, ca estimatia optimista sa se realizeze daca economia nationala este in avant, cea pesimista daca economia este in depresiune, iar cea mai probabila estimatie daca economia functioneaza la un nivel normal. Desigur, este necesar ca suma probabilitatilor asociate cu fiecare rezultat sa fie egala cu unitatea.

Masura traditionala a riscului aplicabila proiectelor individuale este legata de variabilitatea rezultatelor si este definita prin distributia de probabilitate, asa cum se prezinta in Figura v-1. Aceasta reprezinta distributia de probabilitate a rentabilitatii a doua proiecte A si B. Aceste rentabilitati sunt calculate pe baza fluxurilor de numerar prevazute in cazul unor scenarii alternative. O anumita rata de rentabilitate poate fi interpretata ca rata interna de rentabilitate a proiectului, pe baza fluxurilor de numerar asociate. Cu cat distributia de probabilitate a ratelor de rentabilitate prevazute este mai ingusta, cu atat este mai probabil ca rentabilitatea reala sa fie mai apropiata de rentabilitatea asteptata si cu atat este mai mic riscul proiectului. Ca urmare, proiectul B este mai putin riscant decat proiectul A; fiecare dintre rentabilitatile posibile ale proiectului B este mai apropiata de rentabilitatea estimata decat rentabilitatile posibile ale proiectului A.

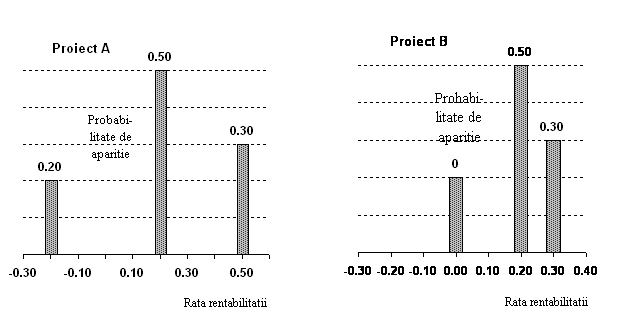
Figura V-1: Graficul a doua distributii de probabilitate

Sa consideram distributia de probabilitate a proiectului A, prezentata in Tabelul III-1. Se observa ca exista 20% sanse de recesiune si, daca aceasta se intampla, proiectul va avea o rata de rentabilitate de -20%. Exista 50% sanse ca perioada sa fie normala si o probabilitate de 30% a unei perioade de avant, in care proiectul va avea o rata mare a rentabilitatii.

Tabelul V-1: Distributia de probabilitate pentru cele doua proiecte

1.2. rentabilitatea estimata (asteptata)

Daca inmultim fiecare rezultat posibil cu probabilitatea de aparitie si apoi insumam aceste produse, ca in Tabelul V-2, obtinem media ponderata a rezultatelor. Ponderile reprezinta probabilitati, iar media ponderata este rata estimata (asteptata) a rentabilitatii, . Rezulta deci ca rata de rentabilitate prevazuta pentru proiectul A este de 21% si de 19% pentru B.

Tabelul V-2: Calculul rentabilitatii estimate pentru cele doua proiecte

Putem spune ca rata estimata a rentabilitatii se poate calcula astfel:

,

unde: este al i-lea rezultat posibil;

este probabilitatea celui de al i-lea rezultat;

n este numarul de rezultate posibile.

Astfel, este media ponderata a rezultatelor posibile, ponderea fiecarui rezultat fiind egala cu probabilitatea de aparitie.

1.3. masurarea riscului : Deviatia standard

Riscul este un concept greu de inteles, existand o multime de controverse in incercarile de definire si masurare a riscului. Exista insa o definitie uzuala, in general satisfacatoare: cu cat distributia de probabilitate a rentabilitatii viitoare este mai ingusta, cu atat este mai mic riscul unei investitii date. Referindu-ne la cele doua proiecte A si B de mai sus si conform acestei definitii, rezulta ca proiectul B este mai putin riscant decat proiectul A, deoarece sansele ca rentabilitatea acestuia sa fie cu mult sub cea asteptata sunt mai mici pentru proiectul B decat pentru proiectul A.

Pentru a fi utila, o masura a riscului trebuie sa aiba definita o valoare, adica avem nevoie de o masura a ingustimii distributiei de probabilitate. O astfel de masura este deviatia standard, simbolizata cu litera "sigma", σ. Cu cat este mai mica deviatia standard, cu atat este mai stransa distributia de probabilitate si, in consecinta, riscul activului espectiv este mai mic. Deviatia standard este radacina patrata a variantei, σ², si se calculeaza dupa formula:

,

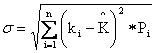unde: k_i = al i-lea rezultat posibil;

= rata estimata a rentabilitatii;

P_i = probabilitatea de aparitie a rezultatului i.

Astfel, deviatia standard este o probabilitate - media ponderata a deviatiei de la valoarea asteptata; ea ne arata cu cat este valoarea reala mai mare sau mai mica decat valoarea asteptata. Daca presupunem, mai departe, ca distributia de probabilitate este continua, astfel ca probabilitatea poate fi estimata pentru fiecare rezultat posibil, atunci putem trasa o curba continua care uneste toate ratele rentabilitatii. Distributiile de rentabilitate pentru doua proiecte, C si D, prezentate in figura de mai jos, sunt exemple de distributii continue de probabilitate. Graficul proiectului C prezinta doua caracteristici ale unei investitii mai favorabile: (1) are rentabilitatea asteptata mai mare si (2) distributia de probabilitate este mai stransa, indicand o dispersie mai mica si, in consecinta, un risc mai mic.

1.4. criteriul "medie-varianta" si aversiunea fata de risc

In figura de mai sus se observa ca proiectul D este preferabil proiectului C, deoarece D are rentabilitatea asteptata mai mare (media) si deviatia standard (si deci varianta) mai mica decat proiectul C. Aceasta ilustreaza un principiu fundamental in finante: criteriul "medie-varianta", prin care, la risc constant, investitorii prefera proiectele cu rentabilitate asteptata mai mare (medie mai mare) proiectelor cu rentabilitate asteptata mai mica si, la aceeasi rentabilitate asteptata, prefera proiectul cu risc mai mic (varianta mai mica) proiectului cu risc mai mare. Aceasta preferinta a investitorilor pentru risc mai mic se numeste aversiune fata de risc. In situatia prezentata grafic mai sus, proiectul D este preferat lui C, deoarece ofera atat varianta mai mica, cat si medie mai mare.

Criteriul medie-varianta se bazeaza pe notiunea generala ca investitorii, in medie, se opun riscului, si, ca urmare, investitiile mai riscante necesita o rentabilitate asteptata mai mare decat investitiile mai putin riscante.

2. riscul de portofoliu si modelul capm

(capital asset pricing model)

Un activ, reprezentand o parte a unui portofoliu, este in general mai putin riscant decat acelasi activ izolat. Acelasi lucru e valabil si pentru investitii: o investitie luata separat este mai riscanta decat un portofoliu de investitii. Acest fapt a fost inclus intr-un cadru general pentru analiza relatiei dintre risc si rentabilitate; acest cadru se numeste modelul CAPM (Capital Asset Pricing Model). Acest model este un instrument analitic foarte important, atat in managementul financiar cat si in analiza investitiilor.

2.1. riscul si rentabilitatea unui portofoliu

Cele mai multe active nu sunt pastrate izolat, ci mai degraba ca parte a unui portofoliu. Astfel, faptul ca o componenta a portofoliului inregistreaza o crestere sau o scadere, nu mai are o importanta atat de mare; importante sunt rentabilitatea si riscul intregului portofoliu, dar desigur, trebuie analizat felul cum fiecare componenta a acestuia afecteaza riscul si rentabilitatea portofoliului din care face parte.

Rentabilitatea estimata a portofoliului, _p, este pur si simplu media ponderata a rentabilitatii estimate a proiectelor individuale din portofoliu, cu ponderile w_j reprezentand proportia din portofoliul total investita in fiecare proiect:

_p= w₁₁ + w₂₂ + w₃₃ +.+ w_nn = ,

unde suma ponderilor este egala cu unitatea.

Riscul portofoliului, σ_p, nu este, in general, media ponderata a deviatiilor standard ale proiectelor individuale care formeaza portofoliul. De obicei, riscul portofoliului este mai mic decat media ponderata a deviatiilor standard (sigma) ale proiectelor. De fapt, teoretic ar putea fi posibil sa combinam doua proiecte, care sunt destul de riscante luate individual, formand astfel un portofoliu care este complet lipsit de risc, cu σ_p= 0. Motivul pentru care aceste doua proiecte pot fi combinate formand un portofoliu fara risc, este ca rentabilitatile acestora evolueaza in contratimp, cand rentabilitatea unuia scade, rentabilitatea celuilalt proiect creste, si invers. Din punct de vedere statistic, rentabilitatile celor doua proiecte sunt perfect corelate negativ, cu coeficientul de corelatie = r = -1. Corelatia este definita ca tendinta a doua variabile de a evolua impreuna.

Opusul corelatiei perfect negative, cu r = -1, este corelatia perfect pozitiva, cu r = +1. Rentabilitatle a doua active, corelate perfect pozitiv ar evolua impreuna si portofoliul constand din doua astfel de active ar fi la fel de riscant ca si activele luate individual. Se poate trage deci concluzia ca diversificarea nu face nimic pentru a reduce riscul, daca portofoliul este format din active coralate perfect pozitiv, spre deosebire de cazul in care activele din portofoliu sunt corelate perfect negativ, caz in care riscul se diminueaza prin diversificare.

In realitate, cele mai multe active sunt corelate pozitiv, dar nu perfect. In aceste conditii, combinarea activelor in portofolii reduce riscul, dar nu il elimina complet. Deci, intre aceste extreme ale corelatiei perfect pozitive si perfect negative, combinarea a doua active intr-un portofoliu reduce, fara sa elimine, riscul inerent activelor considerate individual.

In figura de mai jos, este demonstat efectul diversificarii prin combinarea de active cu diferiti coeficienti de corelatie:

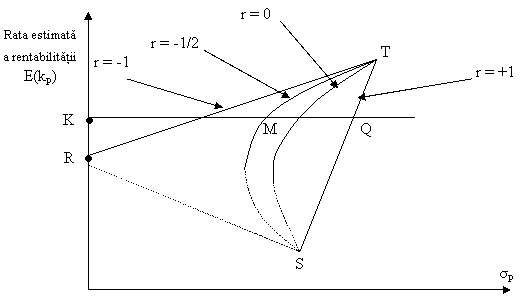
Figura IV-3: Relatia dintre rentabilitatea estimata si riscul de portofoliu

Rata estimata a rentabilitatii portofoliului, E(k_p), este reprezentata pe axa verticala, iar deviatia standard a rentabilitatii portofoliului este reprezentata pe axa orizontala. Portofoliul este construit prin utilizarea unei parti a fondurilor disponibile pentru proiectul de investitii S, iar cealalta parte a fondurilor pentru proiectul de investitii T. Modificand ponderea alocata fiecareia din cele doua proiecte, se obtin diferite portofolii. Cand r = +1, relatia dintre S si T este liniara. Pe masura ce coeficientul de corelatie se indeparteaza de 1, linia care uneste S si T se curbeaza tot mai mult. La extrema, pentru r = -1, exista un set de ponderi pentru cele doua investitii S si T pentru care riscul dispare in intregime. Aceasta situatie este reprezentata de punctul R din figura. Pentru a demonstra importanta diversificarii, sa consideram rentabilitatea estimata a portofoliului, notata K. Daca r = 1, punctul risc-rentabilitate este Q. Pe masura ce coeficientul de corelatie se indeparteaza de +1, se obtine aceeasi rentabilitate estimata a portofoliului, deoarece ponderile nu se schimba, dar riscul total al portofoliului este redus. In figura de mai sus, masura diversificarii este diferenta dintre punctul Q si deviatia standard a portofoliului de-a lungul liniei KQ, pentru un coeficient de corelatie dat. De exemplu, efectul diversificarii, pentru coeficientul de corelatie r = -1/2, este egal cu MQ.

Se ridica intrebarea ce se intampla daca includem mai mult de doua proiecte intr-un portofoliu de investitii? Ca regula generala, riscul de portofoliu se reduce pe masura ce numarul de active din care este format creste. Dar oare am putea elimina complet riscul daca am adauga suficiente active corelate partial? In general, raspunsul este negativ, dar masura in care adaugarea de active in portofoliu reduce riscul acestuia depinde de gradul de corelatie dintre active. Cu cat este mai mic coeficientul de corelatie, cu atat este mai mic riscul ramas intr-un portofoliu mare. Daca s-ar putea gasi un set de active al caror coeficient de corelatie ar fi zero sau negativ, atunci riscul ar putea fi eliminat. In situatia tipica in care coeficientii de corelatie dintre activele individuale sunt pozitivi si mai mici decat +1, riscul poate fi eliminat partial, dar nu total.

Figura de mai jos, generalizeaza cazul cu doua active, pentru un numar mai mare de active N, intr-o diagrama risc-rentabilitate. Presupunand ca nu exsta active cu corelatii egale cu +1 sau -1, relatia dintre riscul de portofoliu si rentabilitate este prezentata in Figura IV-4

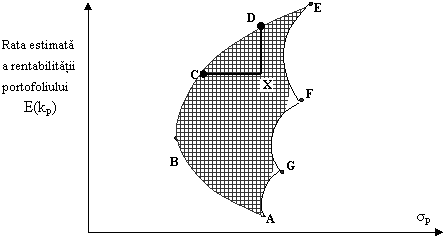
Figura IV - 4 Oportunitatile unui portofoliu format din N active (proiecte de investitii)

Setul ipotetic al tuturor portofoliilor posibile - numit set realizabil - este reprezentat de suprafata hasurata din figura. Vom defini acum un portofoliu eficient ca acel portofoliu care ofera rentabilitatea maxima posibila pentru orice grad de risc sau gradul de risc minim posibil pentru orice rentabilitate estimata. In figura de mai sus, frontiera BCDE defineste setul de portofolii eficiente. Portofoliile aflate la stanga setului eficient nu sunt posibile, deoarece sunt in afara setului realizabil, adica nu exista nici un set de valori ale ratei de rentabilitate pentru care sa ofere portofoliului o rata estimata a rentabilitatii si un risc, care sa fie reprezentate printr-un punct aflat la stanga curbei BCDE. Portofoliile aflate la dreapta setului eficient sunt ineficiente, deoarece un alt portofoliu ar putea oferi fie o rentabilitate mai mare cu acelasi grad de risc, fie un risc mai mic pentru aceeasi rata a rentabilitatii. Pentru a ilustra aceasta situatie, sa consideram portofoliul (punctul) X. Portofoliul C ofera aceeasi rata a rentabilitatii ca si portofoliul X, dar C este mai putin riscant. In acelasi timp, portofoliul D este la fel de riscant ca si portofoliul X, dar D ofera o rata mai mare a rentabilitatii. Se spune ca punctele C si D (si alte puncte pe frontiera setului eficient dintre C si D) domina punctul X[1].

S-a constatat ca, desi riscul individual poate fi diminuat prin diversificarea portofoliului respectiv, un anumit risc ramane intotdeauna, fiind virtual imposibil de diversificat. Acea parte a riscului care poate fi eliminata prin diversificare se numeste risc diversificabil, risc specific companiei (riscul de firma) sau nesistematic. Acea parte a riscului care nu mai poate fi eliminata prin diversificare se numeste risc nediversificabil, risc de piata sau sistematic. Riscul de firma este cauzat de actiuni in justitie, greve, succesul sau insuccesul programelor de marketing, castigul sau pierderea unor contracte majore sau alte evenimente care au loc in cadrul firmei respective. Deoarece aceste evenimente sunt in esenta aleatoare, efectele lor asupra portofoliului de investitii pot fi eliminate prin diversificare (unele evenimente nefavorabile se vor compensa cu altele favorabile). Riscul de piata, pe de alta parte, se refera la razboi, inflatie, recesiuni, variatii ale ratei dobanzii, s.a.m.d. Acesti factori afecteaza toate firmele simultan. Deoarece toate firmele sunt influentate in aceeasi directie de catre acesti factori, acest tip de risc nu mai poate fi eliminat prin divesificare. Astfel, suma dintre riscul de firma si cel de piata se numeste riscul total al unui acti

Dupa cum se stie, investitorii solicita o prima pentru asumarea riscului; cu cat este mai mare riscul asumat, cu atat rentabilitatea ceruta este mai mare. Insa, daca investitorii, adica firmele respective, sunt preocupati, in primul rand, de riscul de portofoliu si nu de riscul fiecarui activ in parte, se naste intrebarea cum ar trebui masurat acest risc individual. Raspunsul oferit de modelul CAPM (Capital Asset Pricing Model) este urmatorul: riscul relevant al unui activ considerat individual este contributia acelui activ la un portofoliu bine diversificat. Activul respectiv ar putea fi destul de riscant daca ar fi considerat individual, dar, daca cea mai mare parte a riscului poate fi eliminata prin diversificare, riscul relevant al acelui activ, reprezentat de contributia lui la riscul portofoliului, poate fi mic.

Acum se naste insa intrebarea daca toate activele sunt la fel de riscante, adica adaugarea lor la un portofoliu bine diversificat va avea acelasi efect asupra riscului portofoliului. Raspunsul este negati Diferitele active vor afecta portofoliul in mod diferit si deci active diferite au diferite grade de risc relevant. Dupa cum am vazut, tot riscul, cu exceptia celui datorat miscarilor pietei, poate fi eliminat prin diversificare. Riscul ramas dupa diversificare este riscul pietei, adica un risc inerent, care poate fi masurat prin gradul in care un proiect dat tinde sa se deplaseze in sus sau in jos impreuna cu piata. Va trebui deci sa gasim o masura pentru acest risc de piata.

2.2. conceptul de "beta"

Tendinta unui activ de a varia impreuna cu piata este reflectata de coeficientul beta, β, care este o masura a volatilitatii activului in raport cu un activ cu volatilitate medie. Coeficientul beta este un element cheie al modelului CAPM. Un activ cu risc mediu este acela care tinde sa varieze, in sus sau in jos, in pas cu variatia pietei si are, prin definitie, un beta egal cu 1 (adica se modifica cu acelasi procent si in acelasi sens cu variatia pietei). Un portofoliu format din astfel de active, avand β =1, va creste sau va scadea o data cu variatiile medii ale pietei si va fi la fel de riscant ca aceasta medie. Daca β ar fi 0,5, atunci activul ar avea jumatate din volatilitatea pietei, iar un portofoliu format din astfel de active va avea jumatate din gradul de risc al unui portofoliu cu β =1. Pe de alta parte, daca β = 2, activul este de doua ori mai riscant decat media, iar un portofoliu cu astfel de active va fi de doua ori mai riscant decat media. Coeficientul beta si deci riscul unui portofoliu este o medie ponderata a coeficientilor beta ai acelui portofoliu:

β_p = w₁β₁ + w₂β₂ + w₃β₃ +.+ w_nβ_n = ,

unde β_p este coeficientul beta al portofoliului, w_i este ponderea activului i, masurata ca raportul dintre suma investita in activul i si suma totala investita in portofoliu, iar β_i este coeficientul beta al activlui i. De aceea, daca se adauga un activ cu un coeficient beta mai mare decat media (β >1) la un portofoliu de risc mediu (β =1), atunci coeficientul beta si deci riscul portofoliului vor creste. Din contra, daca se adauga un activ cu un coeficient beta mai mic decat media (β <1) la un portofoliu cu risc mediu (β =1), coeficientul beta al portofoliului va descreste. Astfel, daca coeficientul beta al unui activ masoara contributia acestuia la riscul portofoliului pietei, coeficientul beta este o masura adecvata a riscului acelui acti

Analiza de mai sus a riscului unui portofoliu reprezinta modelul CAPM - Capital Asset Pricing Model, care este la fel de valabil si pentru un portofoliu format din proiecte de investitii, si se poate rezuma in cele ce urmeaza:

riscul are doua componente, riscul de piata si riscul de firma;

riscul de firma poate fi eliminat prin diversificare; ceea ce ramane este riscul de piata, cauzat de miscarile generale ale pietei, si care reflecta faptul ca toate activele (proiectele) sunt afectate sistematic de anumite evenimente. Riscul de piata este singurul risc relevant pentru un investitor rational diversificat, deoarece acesta a eliminat deja, prin diversificare, riscul de firma;

investitorii se asteapta la o compensatie pentru asumarea acestui risc - cu cat este mai mare riscul cu atat este mai mare rentabilitatea ceruta. Compensatia este, insa, necesara pentru riscul care nu poate fi eliminat prin diversificare;

riscul de piata al unui activ (proiect) este dat de coeficientul beta, care este un indicator al volatilitatii relative a activului (proiectului) respectiv;

deoarece coeficientul beta al unui activ (proiect) determina modul cum acel activ (proiect) afecteaza gradul de risc al unui portofoliu diversificat, coeficientul beta este cea mai relevanta masura a gradului de risc al activului (proiectului) respecti

Trebuie mentionat faptul ca beta trebuie sa reflecte asteptarile investitorilor privind volatilitatea viitoare si nu avem nici o modalitate de a masura cu exactitate aceste asteptari. De aceea, este imposibil sa obtinem estimatii precise ale lui beta. Se pot calcula in schimb valori aproximative pentru beta, pe baza volatilitatii din trecut.

3. linia pietei de capital: relatia dintre risc si rata estimata a rentabilitatii

Este necesar de stiut, la un nivel dat al lui beta, care ar fi rata estimata a rentabilitatii pe care o vor cere investitorii pentru a compensa riscul asumat. In teoria modelului CAPM, linia pietei capitalului ("security market line" - SML) exprima rentabilitatea necesara investitiei ca suma dintre rata de grad de risc zero si un factor de ajustare a riscului pe care investitorii il cer ca o compensatie pentru asumarea riscului. Acest factor de ajustare a riscului unui activ (proiect) dat este obtinut prin inmultirea primei de risc a pietei cu riscul investitiei individuale masurat prin beta. Ecuatia SML este urmatoarea:

k_i = k_RF + β_i (k_M - k_RF),

unde: k_i = rata necesara a rentabilitatii activului i (proiectului i);

k_RF = rata rentabilitatii unui activ lipsit de risc; in acest context, k_RF este, in general, masurat de rata rentabilitatii investitiiilor in titluri (obligatiuni) emise de stat;

β_i = coeficientul beta al activului i (proiectului i); coeficientul beta al activului mediu este β = 1;

k_M = rata necesara a rentabilitatii unui portofoliu format din toate activele, adica portofoliul pietei; k_M este, de asemenea, rata necesara a rentabilitatii unui activ mediu (β =1); in cazul proiectelor de investitii, k_M este rata de rentabilitate medie asteptata in ramura sau sectorul respectiv; β_M este coeficientul mediu de risc inregistrat la nivelul ramurii sau sectorului respectiv;

RP_M = (k_M - k_RF) = prima de risc a pietei; aceasta este rentabilitatea suplimentara, peste rata instrumentelor lipsite de risc, pe care un investitor o cere drept compensatie pentru asumarea unui risc mediu; riscul mediu este dat de β =1; prima de risc a pietei, RP_M, depinde de gradul de aversiune pe care investitorii medii il au fata de risc;

RP_i = β_i (k_M - k_RF) = prima de risc a activului (proiectului i); prima de risc a activului (proiectului) este mai mica, egala sau mai mare decat prima unui activ (proiect) mediu, dupa cum coeficientul beta al activului (proiectului) este mai mic, egal sau mai mare decat 1; deci, daca β_i = β_M = 1, atunci RP_i = RP_M.

Linia pietei capitalului se utilizeaza pentru a determina costul corespunzator al capitalului in analiza bugetelor de investitii. Exista un numar de variabile importante care determina pozitia si panta SML. Variatia acestor variabile influenteaza costul capitalului folosit in analiza bugetelor de investitii. Atat dreapta SML cat si pozitia unei companii pe aceasta dreapta, variaza in timp datorita variatiei ratelor dobanzii, aversiunii la risc a investitorilor, si coeficientilor beta ai companiilor.

Dupa cum stim, dobanda reprezinta "chiria" pentru banii imprumutati, adica pretul banilor. Astfel, k_RF este pretul banilor imprumutati fara risc. Rata instrumentelor financiare lipsite de risc, masurata de rata dobanzii titlurilor guvernamentale, se numeste rata nominala si este formata din doua elemente: (1) o rata a rentabilitatii reale neinfluentate de inflatie, k^* si (2) o prima pentru inflatie, IP, egala cu rata anticipata a inflatiei. Daca ne asteptam ca inflatia sa creasca, atunci trebuie adaugata la rata rentabilitatii reale neinfluentate de inflatie o prima care sa compenseze investitorii pentru pierderea puterii de cumparare, ca rezultat al inflatiei. Astfel, k_RF = k^* +IP. O astfel de modificare face ca noua linie SML sa se deplaseze in sus, paralel cu vechea dreapta SML. Ecuatia SML se poate reprezenta grafic astfel:

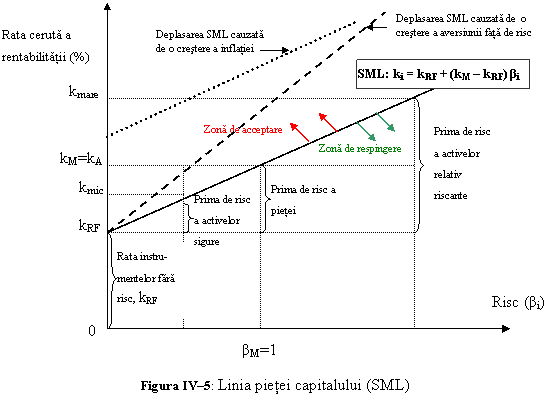
Panta SML reflecta gradul de aversiune fata de risc in economie. Cu cat este mai mare media aversiunii investitorilor la risc, (a) cu atat este mai abrupta panta SML, (b) cu atat este mai mare prima de risc pentru orice actiune si (c) cu atat este mai mare rata necesara a rentabilitatii proiectelor.

SML arata modul in care investitorii sunt dispusi sa faca compromisuri intre risc, masurat de coeficientul beta, si rentabilitatea estimata. Cu cat este riscul mai mare, cu atat mai mare este rata rentabilitatii necesara pentru a compensa investitorii pentru asumarea acestui risc. SML specifica natura acestei relatii.

Daca rata estimata a rentabilitatii unui proiect dat este deasupra SML, rata estimata a rentabilitatii proiectului este mai mult decat suficienta pentru a compensa riscul si proiectul trebuie acceptat. Din contra, daca rata rentabilitatii proiectului este sub SML, proiectul trebuie respins.

4. evaluarea riscului

Pana in prezent, am urmarit identificarea modalitatilor de masurare a riscului, legate fie de distributia de probabilitate si masurat de deviatia standard (sau, unde este cazul, de coeficientul de variatie), fie de riscul sistematic al unei actiuni, bazat pe teoria portofoliului si modelul CAPM. Conceptele prezentate sunt la fel de valabile si daca investitorul este o societate comerciala si investitia este un proiect. Sa urmarim deci, procedurile pentru masurarea riscului proiectelor potentiale si incorporarea acestor informatii in decizia de alocare a capitalului.

Se pot identifica trei tipuri distincte de risc al proiectelor de capital: (1) riscul individual al proiectului, care nu tine seama de faptul ca face parte din portofoliul de active al firmei si ca firma respectiva nu este decat o actiune in portofoliile investitorilor; (2) riscul de firma, care este efectul unui proiect asupra riscului companiei fara a tine cont de efectele diversificarii personale a actionarilor; si (3) riscul de piata sau beta, care este riscul proiectului evaluat din punctul de vedere al unui investitor, in sensul de firma, care detine un portofoliu foarte diversificat. Un proiect particular poate avea un risc individual mare, dar, datorita efectelor de portofoliu, angajarea in acest proiectnu va influenta mult riscul firmei.

Riscul de firma este masurat de impactul proiectului asupra variabilitatii profiturilor firmei. Riscul de firma (sau riscul de corporatie) este important din urmatoarele motive: (1) actionarii nediversificati (in sensul de firme cu un portofoliu de investitii nediversificat), inclusiv firmele mici, sunt mai preocupati de riscul de firma decat de riscul de piata; (2) stabilitatea firmei este importanta pentru manageri, salariati, clienti, furnizori si creditori, comunitatea pentru care activeaza, etc. si de aceea firmele in pericol de faliment sau chiar cele cu profituri si productii reduse au dificultati in atragerea si mentinerea managerilor si salariatilor buni. In plus, atat furnizorii, cat si clientii nu doresc sa depinda firme slabe, iar astfel de firme au dificultati in obtinerea de credite la rate rezonabile ale dobanzii. Acesti factori tind sa reduca profitabilitatea si pretul actiunilor firmelor riscante, facand astfel semnificativ riscul de firma. Riscul de firma influenteaza deci, posibilitatile firmei de a se finanta prin imprumuturi cu cost scazut, de a mentine continuitatea in timp a activitatii si de a evita situatii de criza.

Riscul de piata (beta) este masurat de efectul proiectului asupra coeficientului beta al firmei. Faptul ca un proiect are un grad mare de risc individual sau de firma nu va afecta in mod necesar coeficientul beta al firmei, intr-o masura mare. Insa, daca proiectul are o mare incertitudine a rentabilitatii si daca rentabilitatea este puternic corelata cu rentabilitatea celorlalte active ale firmei si cu majoritatea activelor din economie, proiectul va avea un grad mare de risc, indiferent de tipul acestuia.

Riscul pietei (beta) este important datorita efectului direct asupra pretului actiunilor unei firme: coeficientul beta afecteaza rata rentabilitatii, iar rentabilitatea afecteaza pretul actiunilor.

Analiza riscului este necesara pentru ca ofera o mai buna intelegere a riscului proiectelor si permite managerilor sa ia decizii mai bune de acceptare sau de respingere a proiectelor de investitii. Totusi, aceste masurari ale riscului nu tin seama de riscul de portofoliu si nu specifica clar daca un proiect trebuie acceptat sau respins. Insa, putem folosi modelul CAPM pentru a depasi aceste dezavantaje. Desigur ca acest model are propriile sale limite, dar ofera o cunoastere mai buna a analizei de risc in procesul de alocare a capitalului.

Pe baza ecuatiei SML, si presupunand ca firma utilizeaza pentru investitii numai capitalurile proprii, si ca putem determina coeficientul beta al fiecarui proiect, β_j, costul capitalului unui proiect individual, k_j, poate fi calculat astfel: k_j = k_RF + (k_M - k_RF)β_j, unde notatiile sunt cele specificate anterior. Aceasta sugereaza ca firma ar trebui sa investeasca in proiecte de capital, daca si numai daca aceste proiecte au o rentabilitate estimata de k_j % sau chiar mai mult. Sau altfel spus, firma ar trebui sa utilizeze o rata de actualizare de k_j % pentru a determina VAN pentru orice proiect de investitii de risc mediu considerat. Sa presupunem insa ca angajarea intr-un anumit proiect ar produce o modificare a coeficientului beta al firmei si deci o modificare a costului capitalurilor proprii. Deoarece firma insasi poate fi considerata un portofoliu de active si deoarece coeficientul beta al oricarui portofoliu este o medie ponderata a coeficientilor beta ai activelor individuale, angajarea intr-un anumit proiect ar putea majora coeficientul beta total al firmei, la o valoare situata undeva intre valoarea originala si coeficientul beta al proiectului respecti Valoarea exacta a noului beta va depinde de marimea relativa (ponderea) a investitiei alocata pentru respectivul proiect fata de celelalte active ale firmei. Cresterea coeficientului beta al firmei va cauza o scadere a pretului actiunilor, daca aceasta crestere nu este compensata de o rata estimata de rentabilitate mai mare. Astfel, angajarea in noul proiect produce o crestere a costului capitalului la nivelul corporatiei, iar pentru a impiedica scaderea valorii firmei datorita acestei investitii, rata estimata totala a rentabilitatii firmei trebuie sa creasca si ea.

Riscul individual al unui proiect este masurat de variabilitatea rentabilitatii estimate a proiectului. Riscul individual are, la randul sau, o mare importanta, pentru ca: (1) este mult mai usor de estimat decat riscul de firma si mult mai usor de masurat decat riscul de piata; (2) in majoritatea cazurilor, cele trei tipuri de risc sunt puternic corelate - daca situatia generala a economiei este buna, la fel va fi si situatia firmei, iar aceasta conduce la succesul proiectelor. Astfel riscul individual este, in general, o buna aproximatie a riscului de piata, care este mult mai greu de masurat.

Punctul de plecare pentru analiza riscului individual al unui proiect presupune determinarea incertitudinii inerente a fluxurilor de numerar ale proiectului. Natura distributiei fluxurilor individuale de numerar si a corelatiilor intre acestea determina natura distributiei valorii actualizate nete (VAN) si, astfel, riscul individual al proiectului. Una din tehnicile utilizate pentru estimarea riscului individual al unui proiect este analiza de sensibilitate.

Intuitiv, stim ca o mare parte a variabilelor care determina fluxurile estimate de numerar ale unui proiect se bazeaza pe o distributie de probabilitate, si nu sunt cunoscute cu certitudine. De asemenea, daca o variabila cheie de intrare se schimba, VAN a proiectului se va modifica de asemenea. Analiza de sensibilitate ("sensitivity analysis") este o metoda care indica exact cu cat se va schimba VAN ca raspuns la o modificare a unei variabile de intrare, mentinand constante celelalte elemente.

Analiza de sensibilitate incepe cu o situatie de baza, care este dezvoltata pe baza valorilor estimate pentru fiecare intrare. Analiza de sensibilitate ofera factorului de decizie raspunsuri la intrebarile acestuia privind modificarile ce ar putea interveni asupra pretului unitar de vanzare, productiei vandute, costurilor variabile, etc.

In analiza de sensibilitate, fiecare variabila este modificata cu mai multe puncte procentuale peste si sub valoarea estimata, mentinand celelalte variabile constante; se calculeaza apoi o noua valoare VAN pentru fiecare dintre aceste valori; in final, multimea valorilor VAN este reprezentata grafic, in functie de variabila care a fost modificata. Pantele graficelor arata cat de sensibila este VAN la modificarile fiecarei variabile de intrare; cu cat este panta mai abrupta, cu atat este VAN mai sensibila la o modificare a variabilei. Daca comparam doua proiecte, proiectul cu grafice mai abrupte ale sensibilitatii este mai riscant, deoarece in cazul acelui proiect o eroare relativ mica in estimarea unei variabile, va produce o eroare mare a VAN estimate. Astfel, analiza de sensibilitate ne ofera o mai buna intelegere a riscului unui proiect.

5. REDUCEREA RISCULUI PRIN DIVERSIFICARE

Dupa cum s-a mai mentionat, un activ poate fi destul de riscant deca este pastrat izolat, fara a fi insa foarte riscant daca face parte dintr-un portofoliu bine diversificat. Acest lucru este valabil si in cazul alocarii capitalului; rentabilitatea unui proiect individual poate fi foarte incerta, dar daca proiectul este mic in raport cu firma si daca rentabilitatea sa nu este puternic corelata cu celelalte active ale firmei, proiectul poate sa nu fie foarte riscant din punctul de vedere al corporatiei sau coeficientului beta.

Multe firme fac eforturi serioase de diversificare; acesta este de multe ori un obiectiv al planului strategic pe termen lung. Obiectivele principale ale acestor masuri sunt stabilizarea profiturilor, reducerea riscului la nivelul corporatiei si astfel cresterea valorii actiunilor firmei.

Alocarea capitalului poate afecta riscul de piata al unei firme, riscul de firma, sau ambele. Oricare dintre tipurile de risc care pot interveni sunt extrem de dificil de cuantificat. Astfel, desi s-ar putea ajunge la concluzia ca un proiect este mai riscant decat altul, este dificil de gasit o masura exacta si corecta a riscului acelui proiect. Aceasta lipsa de precizie in masurarea riscului unui proiect face dificila incorporarea riscului diferential in deciziile de alocare a capitalului.

O metoda des utilizata in practica pentru incorporarea riscului proiectelor in procesul de alocare a capitalului este metoda ratei de actualizare ajustate la risc, prin care riscul diferit al proiectelor este abordat prin schimbarea ratei de actualizare. Proiectele cu risc mediu se actualizeaza la costul mediu al capitalului firmei, proiectele cu risc peste medie se actualizeaza la un cost mai ridicat al capitalului, iar proiectele cu risc sub medie la un cost al capitalului mai scazut decat costul mediu al capitalului firmei. Din nefericire, deoarece riscul nu poate fi masurat cu precizie, nu exista o metoda precisa care sa specifice exact cat trebuie sa fie de mare sau mica aceasta rata de actualizare si din aceasta cauza ajustarile riscului fac obiectul unui rationament si sunt intr-o oarecare masura arbitrare.