Parametrii de structura

Parametrii de structura

Frecvente sunt cazurile cand este necesara studierea structurii unei populatii in raport cu o variabila sau alta. Parametrii statistici, in forma cea mai generala, folositi in caracterizarea structurii unei populatii poarta denumirea de valori quantile.

Valorile quantile ale unei serii de repartitie unidimensionale sunt acele marimi inregistrate de variabila X, care impart seria in n parti egale (mai precis imparte populatia in n parti egale). In acest caz se vor calcula p quantile (p = n-1).

Pentru o serie continua, a carei densitate de probabilitate f(x) este cunoscuta, urmatoarea egalitate este satisfacuta de cele p quantile:

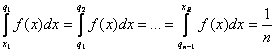(2.22)

unde cele n-1 quantile s-au notat cu q₁, q₂, ., q_n-1.

Relatia (2.22) se particularizeaza pentru cazul seriilor discrete, cand seria este construita cu frecvente relative:

(2.23)

Pentru o serie oarecare, quantila de ordinul p poate fi definita astfel:

sau

Modul de calcul a valorilor quantile difera in raport cu tipul seriei.

Fie o serie de repartitie, care are la baza o variabila X discreta, de urmatoarea forma:

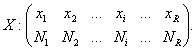(2.24)

Pentru calculul valorii quantile de ordinul , in prima etapa trebuie determinat rangul acesteia:

(2.25)

Se disting doua cazuri:

a) daca pN se divide cu n atunci quantila de ordin p se calculeaza ca o medie aritmetica simpla a valorilor variabilei X, de ordinul rangului si al rangului majorat cu o unitate, dupa cum urmeaza:

(2.26)

b) daca pN nu se divide cu n atunci quantila de ordin p este egala cu acea valoare a variabilei X corespunzatoare parti intregi a rangului majorat cu 1:

(2.27)

In cazul seriilor care au la baza o variabila continua, conform definitiei, cele n-1 quantile trebuie sa satisfaca relatia (2.22). Determinarea quantilelor din asemenea egalitati ar presupune cunoasterea densitatii de probabilitate f(x). Ori in activitatea practica f(x) se aproximeaza prin diverse procedee, implicand un volum exagerat de calcule.

In vederea gasirii unor formule aproximative de calcul a quantilei de ordin se considera o serie de variatie continua, ale carei intervale de variatie nu trebuie sa fie neaparat egale ca lungime:

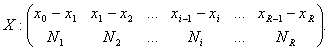(2.28)

In prima etapa se determina rangul quantilei de ordinul conform urmatoarei relatii:

(2.29)

Cunoscand rangul, se poate identifica intervalul in care se afla quantila de ordinul p, numit si intervalul quantilei de ordinul . Cumuland frecventele pe clase pana la egalarea s-au depasirea rangului, conform inegalitatii:

(2.29')

ultima frecventa adunata va corespunde intervalului quantilei de ordinul . Prin urmare, quantila de ordinul p, q_p, se calculeaza conform relatiei:

(2.30)

- reprezentand limita inferioara a intervalului quantilei de ordinul p;

- reprezinta lungimea intervalului quantilei de ordinul p;

- reprezinta frecventa absoluta a intervalului quantilei q_p,

Procedeul de determinare a quantilei de ordinul este acelasi si in cazul in care seria (2.28) este formata din frecvente relative.

Caracterizarea structurii unei serii se poate face utilizand diverse cazuri particulare de valori quantile.

Valoarea mediana (M_e) este si un parametru de structura obtinandu-se ca un caz particular de quantila, cand n=2. Daca pentru o serie se cunoaste M_e (quantila de ordinul 2), atunci structura populatiei poate fi redata astfel:

(2.31)

semnificand faptul ca jumatate din populatia supusa studiului a inregistrat pentru variabila X valori cuprinse intre valoarea minima a lui X si mediana, iar cealalta jumatate din populatie a inregistrat pentru X valori cuprinse intre mediana si valoarea maxima a lui X.

Valorile quartile reprezinta acel caz particular al valorilor quantile pentru care n=4. Cele trei quartile, care se obtin, notate: Q₁, Q₂ si Q₃ sunt acei parametri de structura care impart populatia in patru parti egale.

In raport cu mediana, quartila intai Q₁, se numeste quartila mica (inferioara), quartila a doua Q₂ coincide cu mediana si se numeste quartila mijlocie, iar quartila a treia Q₃ se numeste quartila mare (superioara).

Cunoscandu-se cele trei quartile, rezulta urmatoarea structura a populatiei in raport cu variabila X:

(2.32)

ceea ce semnifica o structurare a populatiei supusa studiului in patru parti egale.

Aceasta inseamna ca 25% din unitatile popupatiei inregistreaza valori pentru variabila X mai mici decat quartila mica, 25% din unitatile populatiei inregistreaza valori, in raport cu aceeasi variabila X, cuprinse intre quartila mica si cea mijlocie, 25% vor avea valori cuprinse intre quartila mijlocie si quartila mare, iar restul 25% din unitatile populatiei vor avea valorile pentru variabila X cuprinse intre quartila mare si valoarea maxima a lui X.