| CATEGORII DOCUMENTE |
| Demografie | Ecologie mediu | Geologie | Hidrologie | Meteorologie |
UNIVERSITATEA ECOLOGICA DIN BUCURESTI
FACULTATEA DE INGINERIE MANAGERIALA
MASTER: Ingineria si Managementul Integrat al Mediului in Activitati Industriale
REFERAT
Sisteme inteligente in ecologie, folosind tehnici neurofuzzy
SISTEME INTELIGENTE IN ECOLOGIE , FOLOSIND TEHNICI
NEUROFUZZY
1.1. ARHITECTURI DE CONDUCERE NEURO-FUZZY. MODELE NEURO-FUZZY
Combinarea retelelor neurale si a regulatoarelor fuzzy are eficienta atunci cand intr-o aplicatie se pot colecta cunostinte partiale privind multimile fuzzy si regulile fuzzy de deductie a comenzii regulatorului. Un regulator fuzzy se proiecteaza pe baza cunostintelor oferite de un expert uman , fara sa fie necesara cunoasterea modelului matematic al procesului,dar regulile de deductie se bazeaza pe cunostintele expertului si pot apare incertitudini in alegerea formei functiei de apartenenta, a numarului acestora si a regulilor de deductie. Modelele neuro - fuzzy pot imbunatati performantele prin folosirea algoritmilor de instruire. Exista doua metode pentru a proiecta modele neuro - fuzzy:
1.1.1.Folosire separata de modele neurale si fuzzy, structuri in care o retea neurala instruieste sau optimizeaza unii parametri ai regulatorului fuzzy. Exista urmatoarele tipuri de variante de a combina aceste 2 modele:
a) Reteaua neurala transmite functiile de apartenenta.Pe baza datelor de intrare se instruiesc retele neuronale care aproximeaza direct functiile de apartenenta sau se instruiesc sa genereze unii parametri ai functiilor de apartenenta, fig.1.1:
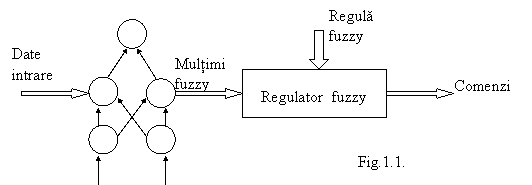
b) Reteaua neurala ofera reguli lingvistice de conducere pe baza datelor de intrare.In acest scop se folosesc algoritmi de grupare "clustering ", ca de exemplu retele Kohonen. Instruierea retelei neurale se face off line, iar multimile fuzzy se definesc printr-o alta metoda, fig.1.2:
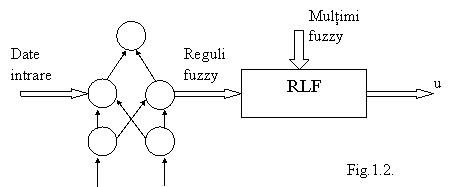
c) Reteaua neurala adapteaza, fig.1.3. on-line parametrii multimilor fuzzy,adica in timpul functionarii acestuia. In acest caz este necesara cunoasterea regulilor fuzzy si a multimilor fuzzy initiale si este necesara definirea unei erori de instruire pentru supervizarea invatarii. Metoda poate fi aplicata si off line daca problema instruirii este fixa. Se pot folosi si retele ca memorii fuzzy asociative.
Fig.1.3.
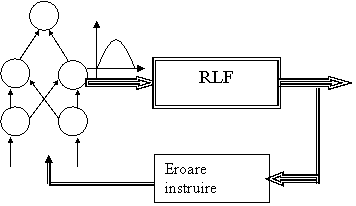
d) Reteaua neurala invata pentru calculul ponderilor in regulile de deductie, fig.1.4. .Aceste ponderi pot fi interpretate ca "importanta" care se da unei reguli si deci se poate modifica iesirea unei reguli. In acest caz regulile de deductie si multimile fuzzy trebuiesc cunoscute. Dar semnatica acestor ponderi nu este cunoscuta.
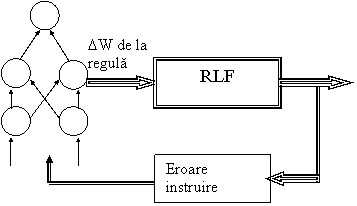
In afara de aceste metode de utilizare separata a modelelor fuzzy si neurale intr-un sistem de conducere, mai pot exista metode cand retelele neurale se folosesc pentru preprocesarea sau postprocesarea intrarilor respectiv iesirile regulatorului fuzzy. Insa aceste variante nu afecteaza optimizarea RLF, ci a sistemului pe ansamblu si deci nu avem un regulator neuro-fuzzy.
1.1.2 Modele hibride neuro-fuzzy
Prin aceasta metoda se proiecteaza o arhitectura omogena ce este de obicei orientata pe retele neurale. Prin aceasta metoda de fapt regulatorul fuzzy se implanteaza cu retele neurale, fig.1.5.

Aceasta metoda are avantajul ca utilizeaza un singur model pentru regulator si nu mai apar probleme de comunicatie intre modelele fuzzy si cele neurale. Ideea acestei metode se bazeaza pe interpretarea bazei de reguli fuzzy a regulatorului , folosind retele neurale. Instruirea retelei neurale se face prin supervizare, ceea ce necesita comenzile exterioare. Daca exista o problema de instruire fixa si procesul tehnologic suporta unele experimentari, atunci instruirea se poate face si on line. Pentru instruire este necesara cunoasterea functiilor sistemului si a unor criterii de apreciere a starii sistemului ca " buna " sau " proasta ". Pentru a instrui o retea neurala este necesar un set de date de instruire sau o functie de evaluare a starilor sistemului.
In concluzie, folosirea uneia dintre metodele prezentate, de proiectare a regulatoarelor sau modelelor fuzzy, se face pe baza analizei urmatoarelor criterii:
daca functiile de apartenenta si regulile de deductie sunt cunoscute partial sau in intregime
daca modelul fuzzy al regulatorului este cunoscut si acesta trebuie implementat
In definirea acestor criterii trebuie avut in vedere daca problema instruirii retelei neurale este definita si daca trebuie alese functiile de apartenenta si daca parametrii acestora sunt initializati.
1.2.OPTIMIZAREA SISTEMELOR DE CONDUCERE CU LOGICA FUZZY FOLOSIND RETELE NEURALE
Regulatorul cu logica fuzzy este definit prin trei elemente:
fuzificare: convertirea valorilor crisp de intrar in valori fuzzy, adica multimi de valori descrise lingvistic
baza de reguli de deductie: convertirea valorilor lingvistice de intrare si valorilor lingvistice de iesire
defuzificare: convertirea valorilor lingvistice de iesire in valori crisp de iesire
Pentru optimizarea unui RLF este necesara cunoasterea acestor trei elemente in raport cu intrarile si iesirile sistemului. Prin optimizarea RLF se urmareste ajustarea functiilor de apartenenta si a setului de reguli de deductie. O metoda de proiectare este " trial and error " care are dezavantajul ca dureaza mult si este definita pentru RLF cu sute de reguli. O alta metoda consta in transpunerea RLF intr-o retea neurala si in optimizarea acesteia printr-o metoda de instruire, dupa care se poate reveni la structura RLF.
a) Convertirea fuzificarii. Se considera ca functiile de apartenenta sunt triunghiulare, pentru ca in acest mod se pot reprezenta mai usor valorile crisp de intrare. Astfel se poate defini un neuron fuzzy, fig.1.6. unde ponderea se defineste prin relatia:
![]() , unde gI>0 si xI o valoare
arbitrara
, unde gI>0 si xI o valoare
arbitrara
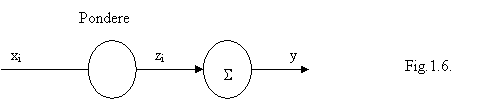
b) Convertirea regulilor de baza. Daca se foloseste regula " IF A THEN B ", cu functiile de apartenenta mA(x) si mB(x), atunci multimea fuzzy rezultata pe universul A B, definita prin
![]()
are o functie de apartenenta, care de exemplu prin metoda MIN este
![]()
daca insa avem mai multe reguli, atunci prin operatia OR. Pentru iesirea RLF se obtine:
![]()
Operatia de generare a regulilor include operatia de max, min care pot fi implementate de neuroni. De exemplu operatia de complement ,sau de negare fuzzy, este definita prin:
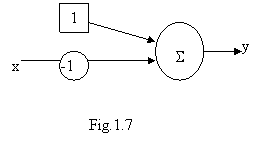
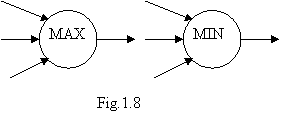
Aceasta operatie de negare fuzzy poate fi implementata prin schema din fig.1.7. Schemele pentru implementarea cu neuroni a operatiilor fuzzy MIN si MAX au la baza folosirea mai multor neuroni, care se reprezinta prin simbolurile din fig.1.8.
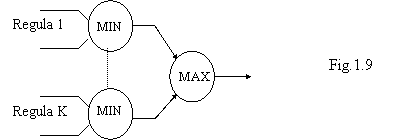
Deci reprezentarea conversiei regulilor de deductie, fig.1.9 include operatii logice fuzzy de MIN pentru fiecare regula si insumarea efectelor acestor reguli prin operatia MAX.
c) Conversia operatiei fuzzy logice de defuzificare
Se considera ca pntru defuzificare, fig.1.10. se adopta metoda centrului de arie, adica valoarea crisp a iesirii este data de relatia:
y = ( åi yimi(yi))/( åI yimi
m
![]()
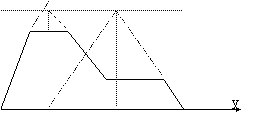
Pentru implementarea relatiei fuzzy pentru defuzificare se utilizeaza scheme cu neuroni, din fig.1.11, unde neuronul care realizeaza operatia de insumare reprezinta numitorul iar cel de iesire executa operatia de impartire.
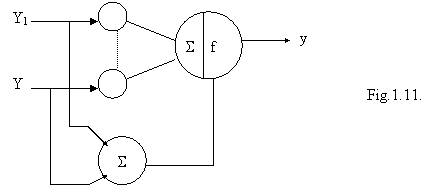
d) Implementarea cu retele neurale ale operatiilor de fuzificare-deductie si defuzificare ale unui regulator fuzzy, fig.1.12. ( pentru cazul unei intrari E, trei functii de apartenenta ABC si o iesire cu 2 f.a. ). Reprezentarea printr-o retea neurala a unui regulator fuzzy necesita patru straturi. Un strat pentru generarea functiilor de apartenenta A, B, C; al doilea strat pentru implementarea functiei IF; al treilea strat pentru functia MAX (de exemplu pentru doua reguli) si stratul de iesire pentru operatia de defuzificare.
e) Operatia de instruire a retelei neurale prin metoda propagarii inverse.
Pentru operatia de instruire prin metoda propagarii inverse este necesar ca functiile de activare sa fie derivabile, in acest scop alegandu-se forma sigmoidala:
![]()
Pentru operatia de instruire, se calculeaza ponderile Wij(k) la fiecare pas in functie de valorile ponderilor la punctul precedent:
![]()
unde a si b sunt constante pentru a controla procesul de instruire, si au valori intre 0 si 1.
Procedura de proiectare a unei retele neurale pentru un RLF, necesita initial alegerea grosiera a unei structuri de regulator, care sa defineasca intrarile si iesirile. In procesul de instruire al retelei neurale se poate folosi experienta expertului de proces tehnologic. Scopul final al instruirii este simularea realitatii conducerii procesului de catre operatorul uman.
1.3. REFACEREA SEMNALELOR INTERMITENTE SAU SATURATE PRIN METODE NEURO-FUZZY
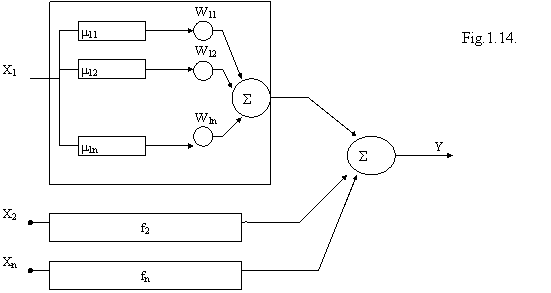
In unele aplicatii semnalele sint saturate, fig1.13, adica limitate fie datorita caracteristicii statice a traductorului, fie datorita unor neliniaritati pe liniile de transmisie a semnalelor. In aplicatii speciale, de exemplu recunoasterea semnalului vocal, saturarea poate surveni de la microfon sau de la proasta alegere a caracteristicii convertorului analog-numeric. In cazul in care semnalul este si intermitent se pune problema refacerii, restaurarii formei semnalului, a predictiei semnalului saturat sau intermitent. In acest scop se pot folosi modele autoregresive, dar pentru semnale neliniare nu sunt utilizabile. Retelele neurale pot fi folosite pentru restaurarea semnalelor saturate sau intermitente, dar acestea necesita mult timp pentru instruire. Pentru reducerea timpului de instruire se pot folosi neuroni neo-fuzzy, o combinatie intre logica fuzzy si retele neurale. Un neo-fuzzy neuron, fig.1.14. are iesirea definita printr-o suma algebrica a unor functii neliniare fI(xI) adica:
y = f1(x1) + .+fn(xn)
Functia neliniara fi(xi) este obtinuta prin deductii fuzzy de forma
![]()
unde Aij este o multime fuzzy a caror functii de apartenenta mij se alege de forma triunghiulara iar Wij este " singleton ", adica cu o valoare mica.
Ca functii de apartenenta se aleg functii triunghiulare complementare , adica pentru orice semnal de intrare xi se activeaza numai doua reguli simultan, iar suma acestora este unu. Folosind metoda de defuzyificare a centrului ariei, iesirea unei functii neliniare este:
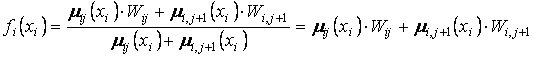
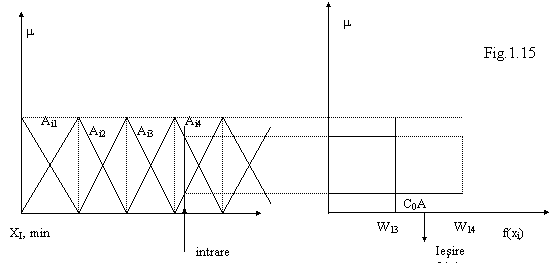 Procesul de detectie prin metoda conturului
de arie este prezentat in fig.1.15, pentru cazul cand functiile de apartenenta
acopera intreg domeniul de variatie al semnalului de intrare:
Procesul de detectie prin metoda conturului
de arie este prezentat in fig.1.15, pentru cazul cand functiile de apartenenta
acopera intreg domeniul de variatie al semnalului de intrare:
Xi
![]()
Daca se noteaza prin y~ iesirea test si prin y iesirea curenta a neuronului , atunci pentru instruire se poate alege functia de eroare:
E = 1/2åk (yk -yk~)2
si se utilizeaza metoda gradientului prezentata. Un neuron neo-fuzzy are caracteristic faptul ca este definit prin reguli lingvistice fuzzy IF-THEN si ca are o viteza mai mare de instruire decat retelele neurale conventionaloe.
Pentru restaurarea unui semnal saturat sau a unui semnal intermitent datorita unor defecte de transmisie, semnalele de intrare aplicate neuronului neo-fuzzy, sunt valori ale acestui semnal de la tactele precedente, memorate prin linii de intarziere.
1.4. SISTEM HIBRID FUZZY NEURAL DE CONDUCERE A UNUI PROCES DE FERMENTATIE
Procesul de fermentatie dintr-un bioreactor este definit printr-o functie de cost de forma:
C(Fin) = a|mmax m(t+1)| + b|sp-s(t+1)| + c|DOsp - DO(t+1)|
unde:
-C(Fin) este functia de cost care trebuie minimizata prin gasirea acelei valori a argumentului pentru care are valoare minima
-Fin viteza de estimare a substratului
-S concentratia substratului ( g/cm3)
m viteza de crestere specifica ( s -1)
-DO oxigen dizolvat ( % )
-a,b,c parametrii fuzzy ai functiei cost
Pentru calculul valorii functiei cost se utilizeaza o retea neurala care sa predicteze valorile parametrilor: m(t+1),s(t+1),DO(t+1) la tactul urmator.In acest scop se utilizeaza o retea neurala cu 15 noduri de intrare la care se aplica semnalele de intrare DO(t), RQ(t), Eg(t), Fin(t) la momentul actual de timp si cele de la momentele (t-1) si (t-2) prin doua elemente de intarziere. Stratul ascuns are 30 de noduri , iar stratul de iesire 3 noduri.De asemenea este necesar proiectarea unui modul fuzzy care sa determine valorile parametrilor a,b,c ai functiei de cost. In acest scop se folosesc trei tabele de adevar pentru fiecare coeficient a, b, c de forma:
DO
|
a |
FMIC |
MIC |
MED |
MARE |
FMARE |
||
|
RQ |
- |
FMARE |
MIC |
MARE |
FMARE |
||
|
MED | |||||||
|
MARE |
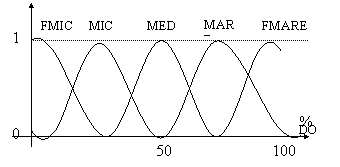
Unde variabilele lingvistice reprezinta: FM - foarte mic, MIC, MED - mediu, FMARE - foarte mare. Cele trei tabele de adevar pentru coeficientii a, b, c sunt completate distinct, in tabel dandu-se cateva exemple pentru unul dintre coeficienti. Pentru variabilele DO si RQ s-au ales functiile de apartenenta din fig.1.16.
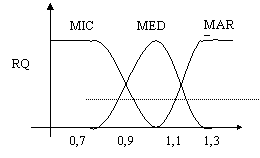
Calculul coeficientilor a,b,c se face prin modelare fuzzy. Pentru aceasta fiecarui coeficient i se asocieaza conform tabelului sau specific o regula de forma :
IF rq ESTE mic AND do ESTE mediu THEN a este mic.
Pentru valorile curente ale parametrilor DO si RQ , conform tabelului de reguli se gaseste functia de apartenenta a parametrului respectiv, de exemplu, si prin operatia de defuzificare, folosind metoda centrului de arie se calculeaza valoarea actuala a coeficientului a.. Operatiile se repeta pentru ceilalti coeficienti b si c gasindu-se valorile acestora. Pentru valorile determinate prin sistemul fuzzy ale coeficientilor a, b, c si pentru valorile predictate de reteaua neurala se calculeaza valoarea functiei de cost. Calculele se repeta pentru mai multe valori ale functiei cost ,determinandu-se astfel referinta optima, pentru care functia cost re valoarea minima. Prin aceasta procedura s-a optimizat procesul dupa o functie de cost.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2673
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved