Geologia si ingineria zǎcǎmintelor de gaze naturale

Geologia si ingineria zǎcǎmintelor de gaze naturale

a) Mǎrimi si unitǎti de mǎsurǎ folosite uzual

Se prezintǎ cateva mǎrimi si unitǎtile de mǎsurǎ folosite in santierul gazeifer astfel :

1) Presiunea se calculezǎ cu relatia :

unde

p = presiunea in : ( at=atmosferǎ tehnicǎ ; atm = atmosferǎ fizicǎ ; Bar , Pa = Pascal )

Interdependenta dintre eceste mǎrimi este urmǎtoarea :

1 atm = 1.033 at ; 1 at = 1 kgf / cm² ; 1 Pa = 1 N /m² = 0,101972 kgf / m²

1 bar = 100.000 Pa = 0,1 MPa (megaPascal) = 1,10972 kgf/cm²

1 bar = 1 at = 1 kgf/cm² ; 1MPa = 10 at = 10 kgf/cm²

2) Presiunea hidrostaticǎ se calculezǎ cu relatia :

unde ;

p_h = presiunea hidrostaticǎ (presiunea unei coloane de fluid) in : ( at. ata. Pa, MPa, bar )

g = acceleratia gravitationalǎ in : ( m/s² si este = 9,8 m /s ² )

ρ = densitatea fluidului ( g / cm³ ; kg / dm³ )

H = inǎltimea coloanei de fluid

3) Greutatea specificǎ se calculezǎ cu relatia 

unde :

= greutatea specificǎ in ; ( gf / cm³ ; gkf / dm³ )

ρ si g = au semnificatiile de la pct.2

4) Presiune hidrostaticǎ functie de greutatea specificǎ se calculezǎ cu relatia 

unde

p_h , H si γ = au semnificatiile de mai sus

5) Viteza de curgere a fluidului se calculezǎ cu relatia 

w = unde :

w = viteza medie in ( m/s ; km /h ; km /s)

S = spatiul parcurs i ( cm . m km )

t = timpul necesar parcurgerii spatiului in ( s ; h ; min )

6) Acceleratia se calculezǎ cu relatia 

a = unde :

a = acceleratia in ( m/s² )

w , t si S = se calculezǎ cu relatia 

7) Debitul unui fluid se calculezǎ cu relatia :

Q = unde :

Q = debitul de fluid in [ dm³ /s ; m³ /s : m³ /h sau Nm³ /h (normali m³ /h )]

V = volumul de fluid vehiculat prin conductǎ in ( cm³ ;m³ ;dm³ sau Nm³ )

t = timpul in (s ; H ; min.)

8) Debitul functie de viteza de curgere se calculezǎ cu relatia 

Q = unde :

A = aria suprafetei de curgere in ( cm² ; dm² ; m² )

w si Q = au semnificatiile de mai sus

9) Ecuatia de continuitate a lui Bernoulli reprezintǎ relatia dintre viteze si sectiuni :

unde :

w₁ , w₂ , w_n = vitezele de curgere a fluidului ( m /s )

A₁ , A₂ , A_n = ariile sectiunilor prin care are loc curgerea

10) Temperatura absolutǎ se calculezǎ cu relatia 

T = 273,15 + t unde :

T = temperatura absolutǎ in [( K ) K = grade Kelvin ]

t = temperatura mediului respectiv in ( ⁰C )

11) Lucrul mecanic se calculezǎ cu relatia 

L = unde :

L = lucru mecanic in [ kgf .m ; J (Joule)] 1 J = ( N = Newton)

d = distanta pe care are loc deplasarea ( m ; km ; cm)

12) Puterea    se calculezǎ cu relatia 

unde :

P = puterea in ( J /s ; w =Watt ; kw ; cP = cal putere ) 1 J/s = 1 w si 1 kw = 1,36 cP

L si t = lucru mecanic si timpul cu aceleasi unitǎti de mǎsurǎ.

13) Vascozitate dinamicǎ este specificǎ unui fluid afalt in regim de curgere laminarǎ :

Fluidul are vascozitatea dinamicǎ de 1 Ns/m² atunci cand douǎ suprafete de 1 m² dintr-un fluid

aflate la o distantǎ de 1 m una fatǎ de cealǎlaltǎ si sub actiunea unei forte de 1 N , o suprafatǎ se miscǎ fatǎ de cealǎlaltǎ cu o vitezǎ de 1 m/s

= vascozitate dinamicǎ ( poisse = 1g/cm .s ) 1 poisse = 0,1Ns/m² )

14 ) vascozitate cinematicǎ se calculezǎ cu relatia 

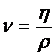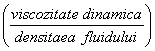; unde :

= vascozitate cinematicǎ in [ m²/s ; Stokes (St) ; )

b) Geneza gazelor naturale si a petrolului

Zǎcǎmintele de petrol si gaze naturale se gǎsesc in medii poroase si permeabile.

1) Cateva precizǎri relative la gazele naturale

a)     Hidrocarburǎ : combinatie organicǎ constituitǎ din carbon si hidrogen care se poate afla in stare de agregare gazoasǎ , lichida si solidǎ

b)    Bitumene naturale ; existenta hidrocarburilor in cele 3 stǎri de agregare prezentate mai sus , in proportie variabilǎ, poartǎ denumitre de bitumene naturale Carecteristic bitumenelor naturale gazoase este faptul cǎ metanul (CH₄) este cel mai rǎspandit (aprox. 90%) si ocupǎ spatiile mediului poros si permeabil aferent zǎcǎmintalor de gaze naturale.

Aceste bitumene gazoase pot forma asǎ numitele zǎcǎminte de gaze libere.

- Gazu metan ( CH₄) poate fi intalnit si sub formǎ de acumulǎri la partea superioarǎ a orizontului cu petrol formand asa numita " cupolǎ de gaze " sau "gaz capul " zǎcǎmintelor de petrol, sau poate fi dizolvat zǎcǎmant

- Sunt cazuri cind gazele , aflate libere in "gaz cap" sau dizolvate in petrol , contin si alte gaze ca etanul , propanul , butanul ,etc. denumindu-se " gaze asociate" In aceste gaze asociate preponderent este metanul (CH₄)

- In afarǎ de gazele libere si asociate in unele zǎcǎminte mai existǎ si 'gazele condensate'

care se extrag din zǎcǎmintele cu condensat

Gazu metan se mai intalneste si in zǎcǎmintele de cǎrbuni sau in gazele ce rezultǎ din activitǎtile vulcanice

In functie de compozitia lor gazele se pot clasifica in :

a)     gaze sǎrace sunt formate din predominant CH₄ si un continut redus de hidricarburi grele

b)    gaze bogate in compozitie pe langǎ CH₄ se aflǎ in diferite proportii si hidrocarburi grele in stare de vapori

2) Ipoteze privind originea gazelor naturale

In ce priveste geneza zǎcǎmintelor de gaze naturale sunt 2 ipoteze ;

a) Geneza anorganicǎ se bazeazǎ pe ideea cǎ o intensǎ activitate vulcanicǎ ar fi generet in urma unor reactii chimice cel putin CH₄ . Reactiile chimice ce au avut loc in conditii de temperaturi si presiuni mari au generat aceste hidrocarburi . Si in Romania sunt geologi care sustin aceastǎ teorie ,

b) Geneza organicǎ tot mai multi cercetǎtori inbrǎtiseazǎ aceaste teorie de genezǎ a hidrocarburilor . Materia primǎ de origine organicǎ cum ar fi ( grǎsimila , protinele , celuloza etc.) sub influienta unor factori (temperaturǎ si presiuni mari , lipsa aerului , prezenta bacteriilor anaerobe , miscǎri tectonice etc.) s-au transformat in hidrocarburi .

S-au facut si unele demonstratii de obtinere a hidrocarburilor in anumite conditii de laborator ca

obtinerea de hidrocarburi gazoase si lichide prin distilarea ficatului de morun (sf, sec.XIX - lea)

S-au identificat mai ales in petrol existenta unor substante colorate (porfirinele) , componente de bazǎ din sange si frunze, precum si (hormoni ) produsi secretati de unele tesuturi care contribuie la finctionarea organismului., ce denotǎ originea organicǎ a hidrocarburilor si a petrolului

Materia primǎ organicǎ de origine acvaticǎ se compune din

a)     planctin vegetal (alge moleculare)

b)    plancton animal (radiolarii)

c)     necton 9o intraegǎ gamǎ de pesti

d)    bentos (diferite specii de scoici si corali)

- S-a constatat cǎ o diatomee in conditii prielnicein 8 zile un volum = volumul Terei

- In zona Atlanticului la intersectia curmtilor Labradorului cu Golfstreeam au murit pesti care

au generat un strat de cadavre cu L = 500 Km , l = 100 km si H = 1, 8m

Formarea hidrocarburilor este dependentǎ de

Factorul biologic (organisme si microorganisme )

Factorul biochimic ( bacterii anaerobe)

factorul geochimic ( separarea functie de densitate a produsilor unui zǎcǎmant)

Fazele posibile de constituire a bitumenelor sunt prezentate in figurile de mai jos :

H₂O cu mil si materie    H₂O

I primǎ organicǎ

II

zonǎ de fitoplancton

mil argilos marnos

zonǎ de zoooplancton    mil protector zona de formare

bitumenelor si

a apei de zǎcǎmant

Clasificarea rocilor in care iau nastere bitumenele

Existenta si stabilitatea zǎcǎmintelor implicǎ existenta urmǎtoarelor tipuri de roci

A)   Roca mamǎ este roca in care au loc transformǎrile substantei organice in prezenta sedimentului minaral in bitumene fixe sau mobile

B)   Roca rezervor sau magazin este roca in care sunt cantonate hidrocarburile . Roca este poroasǎ si hidrocarburile se aflǎ in porii ei Aceste hidrocarbiri pot fi cedate datoritǎ proprietǎtilor roacii (porozitate , permeabilitate, saturatie )

Portiunea rocii rezervor saturatǎ cu hidrocarburi gazoase si lichide = COLECTOR Exemple de roci rezervor : calcare fisurate , dolomite , gresii , nisipuri fine , nisipuri grosiere , nisipuri marnoase etc.

C)  Roca protector Dupǎ denumire este roca care are rolul de a proteja atat la partea superioarǎ cat si cea inferioarǎ acumulǎrile de petrol si gaze. Aceastǎ rocǎ este suficient de groasǎ si rezistentǎ la deformatii precum si impermeabilǎ

Exemple de roci protector : calcarele , argilele , sarea , marnele deci roci compacte.

Existenta acestor roci a dus in timp la formare urmǎtoarelor configutatii geologice :

a)     complexe gazeifere

b)    straturi productive - unitǎti hidrodinamice bine definite ale complexelor gazeifere

Lipsa rocilor protectoare coroboratǎ cu miscǎri tectonice degradarea zǎc. de gaze materializatǎ prin aparitia emanatiilor de gaze ( zona Buzǎu , Corunca , Dumbrǎvioara)

Clasificarea zǎcǎmintelor de gaze naturale

Zǎcǎmintele reprezintǎ acumulǎri de gaze , de petrol sau de gaze si petrol , ocupand un volum bine definit si care este izolat de roci impermeabile

In Romania se foloseste o clasificare in care rezervoarele sau colectoarele naturale de hidrocarburi sunt impǎrtite in 3 grupe care la randul lor se impart in subgrupe iar acestea se impart in genuri astfel :

1) Zǎcǎminte stratiforme - specific acestor zǎcǎminte este cǎ sucesiunea de straturi productive si impermeabile are aproximativ aceeasi grosime si inclinare constantǎ pe o intindere mare Acestea pot fi usor de modelat si de exploatat si sunt de 2 feluri ;

a) zǎcǎminte stratiforme slab boltite

b) zǎcǎminte stratiforme puternic boltite

Zǎcǎminte Masive - specific acestor zǎcǎminte este faptul ca intercalatiile de roci impermeabile lipsesc. Zǎcǎmintele sunt delimitate la partea superioarǎ de roci impermeabile iar la partea inferioarǎ de catre apa de zǎcǎmant bine conturatǎ . Apa avanseazǎ in timpul exploatǎrii hidrocarburilor. O exploatare nerationalǎ duce la formarea conurilor de apǎ sau la inundarea zǎcǎmintelor.

3) Zǎcǎminte delimitate litologic - specific acestor zǎcǎminte este faptul ca acestea sunt inconjurate din toate pǎrtile de roci impermeabile sau nisipuri fine imbibate cu apǎ Aceste zǎcǎminte nu sunt de mare anvergurǎ dar sunt importante d.p.d.v. economic si sunt in Moldova. Ele se epuizeazǎ repede si puneraea in functiune a unor astfel de sone este groaie.

Definirea rezervei si a resursei

Resursa acea cantitate de gaze care se gǎseste intr-un zǎcǎmant

Rezerva acel volum de gaze ce poate fi adus la suprafatǎ in conditii de remtabilitate economicǎ. DECI  Resursa > Rezerva

Datoritǎ retentiei capilarelor nu se poate exploata tot :

La petrol se poate exploata pana la 50% din resursǎ

La gaze se poate exploata pana la 80 - 85 % din resursǎ

Parametrii fizici ai zǎcǎmintelor de gaze naturale

Acesti parametrii impreunǎ cu altii contribuie la evaluarea -REZERVEI RECUPERABILE-

a gazelor naturale cantonate in zǎcǎminte.

Principalii parametrii sunt :

porozitatea

permeabilitatea

temperatura

presiunea

Porozitatea

Porozitatea este proprietatea unor medii de a avea spatii lipsite de materie solidǎ - pori

Hidrocarburile sunt cantonate in porii rocilor colectoare sub o anumitǎ temperaturǎ si presiune.

Porii sunt niste canale care comunicǎ sau nu intre ele cu dametrul (D << 1 mm ) deci sunt capilari sau microcapilari . Din aceastǎ cauzǎ nu toate hidrocarburile pot fi aduse la suprafatǎ deoarece asupra moleculelor de hidrocarburi actioneazǎ forte capilare si forte intermoleculare.

Relatiile de calcul a porozitǎtii

Orelatie de calcul este : n = 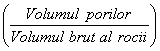unde n = porozitatea in (%)

Dar V_b = V_solid + V_porilor V_solid = V_brut - V_pori si inlocuind In (1) se obtine cǎ porizitatea

n = 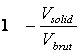sau n = Dacǎ se scrie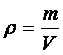

si inlocuind pentru pori si brut se obtine n = in (%)

Aranjarea porilor  : In modelarea teoreticǎ a poriozitǎtii se folosesc 2 modele:

a) aranjare cubicǎ - pentru acest mod de aranjare n = 47, 64 % dar in realitate este mai micǎ

= cu 20 - 25 %

b) aranjare romboedricǎ - pentru acest mod de aranjare n = 25,55 %

In realitate ; n ( 5 - 40 ) %

Porozitatea poate fi asociatǎ unei functii continue de de coordonate n = n (x,y,z )

Dacǎ ; n (x,y,z) = ct. mediul este poros omogen

Compresibilitatea mediului proprietatea corpurilor de a-si micsora volumul sub actiunea fortelor de compresie . Se exprimǎ prin coeficient de compresibilitate .

Compresibilitatea brutǎ a rocii colectoare este datǎ de relatia

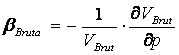unde V_Brut = volumul brut  si p = valoarea presiunii aplicatǎ rocii

Dar : V_b = V_s + V_p se poate scrie ;

Unde _b = compresibilitatea rocii ; _p = compresibilitate porilor ; _s = compresibilitate solid

Compresibilitatea influienteazǎ porozitatea si permeabilitatea rocilor. (ambele sunt inversproportionale cu compresibilitatea) Compresibilitatea se mǎsoarǎ in 1/bar sau bar ^-1

Compresibilitatea rocilor are importantǎ mare in stabilirea formelor de energie de zǎcǎmant in special in regim elestic sau cand dislocuirea este determinatǎ de destinderea apei.

Permeabilitatea este o proprietate adiacentǎ curgerii fluidelor prin medii poroase sub actiunea unui gradient de presiune in conditiile in care mediul poros este saturat in fluid.

Nu intotdeauna mediile cu o porozitate mare au si permeabilitate mare. (ex. spuma de mare)

Tensiunile interfaciale care apar in mediul poros permeabil saturat cu hidrocarburi sunt hotǎratoare in exploatarea panǎ la un anumit nivel a zǎcǎmantului . Mediile in care sunt cantonate hidrocarburile trebuie sǎ permitǎ miscarea hidrocarburilor dintr-un loc in altul. sub actiunea unei forte de presiune. Dacǎ nu existǎ presiune de zǎcǎmant fluidele nu pot trace dintr-un loc in altul. Si permeabilitatea se poate dovedi si calcula ca si porozitatea.

Permeabilitatea a reprezentat obiect de studiu pentru ing. Francez Henry Darcy care a constatat cǎ mediul poros - permeabil influenteazǎ filtrarea .

Darcy a constatat cǎ: Debitul unui fluid in curgere este proportional cu suprafata de curgere , cu diferentǎ de presiune aplicatǎ esantionului de curgere si cu un factor de permeabilitate specific fiecǎrui mediu dar este inversproportional cu lungimea segmentului poros in care are loc curgerea si cu viscozitate dinamicǎ a fluidului

Matematic se poate scrie :

Q = Deci ;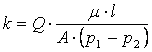

Q = debitulde lichid in ( cm²/s) A= aria suprafetei de curgere a fluidului (cm²)

l = lungimea segmentului poros (cm) =viscozitate cinematicǎ (cP = centipoisse)

k = permeabilitatea mediului (D)

p₁ si p₂ = presiunile de intrare si iesire din mediul poros permeabil ( kgf /cm² )

1 Darcy reprezintǎ permeabilitatea unui mediu prin care circulǎ un lichid cu vascozitatea de 1cP

printr-o arie de 1 cm² sub o diferentǎ de presiune de 1kgf/cm² pe o lungime de 1 cm si realizeazǎ un debit de 1 cm³/s

1D = 0,981 x 10 ^{- 12} m² Submultiplii 1D = 1000 D

Deoarece permeabilitatea rocilor colectoare de cele mai multe ori este mult sub 1Darcy atunci se folosesc submultiplii acestuia . astfel pt. gresia Kliwa k = 30 -50 D iar pt. nisipuri 100 - 2000 D.

Permeabilitatea mediului fatǎ de faza gaz

Permeabilitatea mediului (a rocii ) diferǎ funcie de amestecul de fluid ce trece prin el.

Uneori permeabilitatea unui monogaz poate fi mai micǎ ca a unui amestec si este functie de fazele ce sunt obligate sǎ tracǎ prin rocǎ.astfel :

a) la gaze panǎ la 200 bar permeabilitatea k inversproportionalǎ cu ( p)²

b) la lichide pana la 200 bar permeabilitate k inversproportionalǎ cu ( p)

k Q_gaz

Dacǎ existǎ un p >>> 0

Primul strat de gaze aderǎ la peretele capilarului si celalalte molecule se miscǎ mai repede deci creste debitul .

Atat porozitatea cat si permeabilitatea sunt functii continue de punct

Un zǎcǎmant poate fi exploatat prin mai multe sonde care se aflǎ la anumite distate intre ele . Sondele isi impart suparefata productivǎ a unui zǎcǎmant in cercuri relativ egale . Ele pot avea productii egale sau inegale din cauza variatiei porozitǎtii stratului. De aceea s-a admis cǎ porozitatea este o functie continuǎ pe cele 3 axe de coordonate (x,y, z)

Un zǎcǎmant poate fi impǎrtit in mici unitǎti de volum care au ca si coordonate (x_{i ,}y_{i ,}z_i ) si se poate determina astfel porozitaea cat si permeabilitate acestuia cat mai exact.

Prin extrapolare se poate spune cǎ un cubulet are porozitate " n " precum si porozitatea " k ". Prin integrare triplǎ de volum se poate in domeniu rezonabil sǎ se facǎ calcule ingineresti de rezervǎ

V_{calculat = 1}

y

1

x

1 = punct de coordonate (x_i,y_i,z_i)

Tipuri de permeabilitate

a) permeabilitatea absolutǎ sau totalǎ (k) = suma permabilitǎtilor tuturor canalelor si microcanalelor existente in rocǎ

b) permeabilitatea efectivǎ = suma permabilitǎtilor tuturor canalelor si microcanalelor prin care are loc curgerea

c) permeabilitatea efectivǎ de fazǎ = proprietarea mediului poros de a permite curgerea mai multor fluide existente in rocǎ ( k_gaze = permeb. pt gaze , k_a = p.pt apǎ , k_{t c} = p.pt.titei ,condesat)

d) permeabilitatea relativǎ = k_efectivǎ / k_absolutǎ (are valori intre 0 - 1)

Raportul intre permeabilitatea relativǎ pentru o fazǎ si vascozitatea acestuia se numeste mobilitatea fazei respective Deci se poate scrie :

M_g = M_a = M_{titei sau condensat} =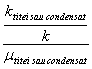

Saturatia in fluide (hidrocarburi

Dacǎ spatiul poros este ocupat in totalitae de fluide (gaz,apǎ) se spune cǎ roca este saturatǎ in fluide .

Deci saturatia = raportul volumul porilor ocupati de fluid / volumul total al porilor din rocǎ

S_{gaze =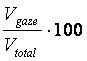} S_apa = S_total = S_gaze + S_ap unde :

S_gaze = saturatia porilor in gaze ; S_apa = saturatia porilor in apǎ : S_totala = saturatia tot a rocii

V_apa = volumul porilor saturati cu apa ; V_gaz = volumul porilor saturati cu gaz

O cantitate apreciabilǎ de apǎ de zǎcǎmant rǎmane legatǎ de porii capilarelor cu dimensiuni mici si aceasta se numeste " apǎ interstitialǎ " sau remanentǎ (intre 10 - 30 %)

Valorile precise ale saturatiei in fluide , ale porozitǎtii si permeabilitǎtii se stabilesc de laboratoare specializate si cu dotare performantǎ . Fluidele se extrag din carote prin diferite procedee mǎsurandu-se greutatea si volumul lor iar rezultatele se transpun in conditii de temperaturǎ si presiune de zǎcǎmant . Valorile determinate pot fi alterate de apa din noroiul de foraj , de noroiul de foraj sau de lichide prtroliere cand forajul se efectuiazǎ cu noroi ce contin astfel de fluide. Pt. a evita aceste neajunsuri in laborator se cautǎ sǎ se extragǎ toate fluidele din carotǎ si se satreazǎ in continuarie cu apǎ sǎratǎ. Se supune carota la presiune panǎ se extrage si aceastǎ apǎ sǎratǎ. Apa care nu a putut fio extrasǎ = apǎ remanentǎ sau interstitialǎ.

Intr- un zǎcǎmant fluidele conforn legii gravitatiei

la parte superioarǎ (in boltǎ sau cupolǎ ) - gazele

la mijloc (pe anticlinal) - titeiul

in parte de jos (pe sinclinal) - apa

In roca colectoare datoritǎ fortei de ascensiune capilarǎ apa urcǎ in anumite conditii panǎ la o anumitǎ inǎltime in zona saturatǎ cu gaze formand " zona de tranzitie apǎ - gaz "

Presiunea de zǎcǎmant si temperatura de zǎcǎmant

A)   presiunea de zǎcǎmant

Ecuatia fundamentalǎ in exploatarea zǎcǎmintelor de hidrocarburi este de forma :

E = F (R,T,P,V, t) unde t = timpul geologic ; (V,P si T) = ale mediului

R = alcǎtuirea structuralǎ a mediului

Cunoasterea presiunii de zǎc. = importantǎ deosebitǎ pentru problemele formǎrii si a prioectǎrii exploatǎrii zǎc, de hidrocarburi.

Presiunea de zǎcǎmant joacǎ rolul de motor in exploatare hidrocarburilor , ea diferǎ de la un orizont productiv la altul .

Apǎsarea pachetelor de rocǎ asupra unui punct imaginar (aflat la o anumitǎ adincime ) se numeste presiune litostaticǎ ; Se calculeazǎ cu relatia

p_{litostatica = 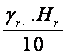r} = greutatea specificǎ a rocii ; H_r = adincimea la care este roca

Presiunea litostaticǎ care actioneazǎ la o dist. H este normal sǎ actioneze si asupra fluidului din rocǎ . In realitate in marea majoritate a cazurilor , stratul protector si impermeabil s-a deteriorat

lent in timp ceea ce a dus la descǎrcarea presiunii panǎ la valoarea de inmagazinare a rezervor.

Valoarea presiunii fluidelor din pori este asimilatǎ cu inǎltimea unei coloane de H₂O de zǎcǎmint consideratǎ de la suprafatǎ pinǎ la adicimea la care este stratul poros- permeabil : p_{initialǎ de zǎcǎmint =} unde H = adincimea la care sunt fluidele in zǎcǎm.

p = . g = _a    unde ; = densitate fluid :

H = adincimea la care se calculeazǎ presiunea

_a = greutatea specificǎ a apei

Deci ; p_{hidrostaticǎ = apa} . H

p _{litostaticǎ = litostaticǎ} . H

P_{litostaticǎ medie} = in ( at ) si P_hidrostatica = in atmosfere

_{litostatica medie} > _apǎ P _litostaticǎ > P _{hidrostaticǎ}

Dacǎ considerǎm cǎ _litostaticǎ = 2,5 kgf/dm³ si H = 3000 m atunci

P_litostaticǎ = iar P_hidrostatica = = 318,6 at

Valoarea medie a presiunii statice de zǎcǎmant se determinǎ cu relatia :

P_{mediu de zǎcǎmint} = unde :

p_staticǎ = presiunea staticǎ in condiii de zǎcamint a sondei " i "

h_i = grosimea efectiv productivǎ a sondei " i "

Anomalii de presiune

Acestea pot fi anomalii pozitive si negative Se poate scrie cǎ :

P_{initialǎ de zǎcǎmint} = P_{la limita gaz - apǎ} P_{suplimentarǎ}

Fuctie de " P_{suplimentarǎ} " se dicting 2 cazui :

a) Dacǎ P_suplim. < 0 atuncu P_iz = P_{limita g-a} - P_s anomalie de presiune negativǎ

b) Dacǎ P_suplim. > 0 atuncu P_iz = P_{limita g-a} + P_s anomalie de presiune pozitivǎ

Cauzele acestei anomalii pot fi :

1) cresteri anormalle ale temperaturii

2) rectii chimice la temp. ridicate ale zǎcǎmintului

3) cutremure de pǎmant - tasǎri ale scoartei

+p_s

- p_s

p_iz p_ag p_ag p_iz

gaz gaz

apǎ apǎ

Anomalie de presiune Anomalie de presiune

negativǎ pozitivǎ

Schema celor 2 tipuri de presiune

Nu intotdeauna o presiune semnificativǎ de zǎcǎmant dece la o productie spectaculoasǎ de CH₄

Date despre presiuni in regim static

Zǎcǎmintele sunt supuse chiar in timul exploatǎrii la diferite regimuri :

a) regim static - sonda este opritǎ (are loc o redistribuire a presiunii pe zǎcǎmant in sensul

uniformizǎrri acesteia in strat) pilniile depresionare (formate in timpul extractiei cautǎ sǎ se

se aplatizeze . Variatia in timp a presiunii de zǎcǎmant este nulǎ

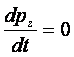
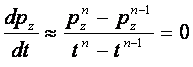deoarece iar

n , n-1 . reprezintǎ trepte temporare

E posibil ca in faza initialǎ p_z1 p_z2 p_zn dar cand t infinit

p_z1 p_z2 p_zn (se egalizeazǎ pe strat)

Inainte de mǎsurarea presiunii statice se iau unele mǎsuri pentru a compensa scoaterea din functiune a sondelor pentru compensarea productiei acestora.

Determinarea noii valor a presiunii statice de zǎcǎmant se face dupǎ mǎsurǎtori cu formula :

P_{mediu de zǎcǎmint} = (semnificatiile lui p si h sunt sus)

Date despre presiune in regim dinamic

Productia oricǎrui orizont de hidrpcarburi fluide este rezultatul a unor forme de energie :

a)     energie naturalǎ - care existǎ in zǎcǎmant

b)    energie sulpimentarǎ - introdusǎ sau generatǎ in zǎcǎmant

Parametrii regimului dinamic sunt :

a)     valori de presiune prelevate in regim dinamic

b)    debite de productie zilnice si cumulative de gaze extrase.

Persiunea se preleveazǎ de la " tubing " si de la " coloanǎ " si reprezintǎ puntea de legǎturǎ intre om si zǎcǎmant

Cu ajutorul parametrilor [prelevati in regim static si dinamic] cǎrora li se asociazǎ si alte date adiacente se intocmesc studii complexe de zǎcǎmant

Aceste studii abordeazǎ probleme cum sunt :

a)     date generale asupra structurii gazeifere

b)    consideratii asupra colectorului si a fluidelor continute

c)     calculul rezervelor de gaze

d)    evaluarea factorului de recuperare a rezervelor

e)     evaluarea declinului de productie a zǎcǎmintului

f)      posibilitǎti de a continua cercetarea zǎcǎm.

Temperatura de zǎcǎmant

Prin cecetǎri experimentale temperatura creste cu inaintarea in adincime la fiecatre 100 metri cu 3,03 ⁰C.

Gradientul geotermic se exprimǎ prin relatia : 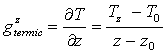unde :

T_z = temperatura la adincimea " z "

T₀ = temperatura medie anualǎ la locul unde se fac mǎsurǎtori

Deoarece temp. poate varia dupǎ cel 3 axe se poate scrie ec. generalǎ a gradientului geotermic

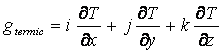
S-a constatat cǎ temperatuar unui zǎcǎmant rǎmane constantǎ

Existǎ si anomalii de temperatura (pozitive - cimpia Banatului si Crisurilor de 60 ⁰C la 1000-1500 metrii, negative - bazinul Siretului si a Dunǎrii 20 ⁰C la 1000 metri)

Mǎsurarea temperaturii de zǎcǎmant

Temp. de zǎcǎmant se mǎsoarǎ cu inregistratoare de adincime care se introdunc in sondǎ .

De regulǎ variatia temperaturii cu adancimea este linearǎ si conrespunde gradientului geotermic din zona respectiva cand viteza de fitratie raportatǎ la un timp suficient de lung tinde cǎtre zero

In cazul in care sonda produce rezonabil , datoritǎ vitezei mari de filtratie are loc o destindere a gazelor si temperatura scade. Datoritǎ acestor diferente de temperatuǎ de adincime este posibilǎ detectarea zonelor care produc apǎ de zǎcǎmant .

Ca aplicatii ale mǎsurǎtorilor de temperaturǎ

( la sondele netubate

a)     detectarea straturilor de gaze - prin expandare produc o rǎcire a zone din dreptul stratului productiv

b)    detectarea straturilor de apǎ - in zona de pǎtrundere a apei in sonda se produce o crestere bruscǎ de temperaturǎ si este cu atat mai mare cu cit creste cantiatea de apa.

(la sondele tubate) - stabilirea zone de curgere a apei in spatele sondei

- determinarea nivelului de ciment in spatele coloanei testate

PROPRIETATI ALE GAZELOR NATURALE

Gazele naturale sunt sisteme de hidrocarburi care se aflǎ in zǎcǎmant su formǎ de vapori :

Din prisma ingineriei de zǎcǎmant g. naturale pot fi :

a)     G. naturale neasociate - sunt sisteme de hidrocarburi aflate in zǎcǎmant sub formǎ de gaze libere ( in absenta petrolului sau a condensatului )

b)    G. naturale asociate - sunt sisteme de hidrocarburi aflate in zǎcǎmant sub formǎ de gaze libere mǎrginite de o zonǎ saturatǎ in petrol sau codensat

c)     G. naturale dizolvate - sisteme de hidrocarburi care in conditii naturale sunt sub formǎ de vapori dar in cond. zǎcǎmant sunt dizolvate in petrol

d)    G. naturale injectete - sunt sub formǎ de vapori si sunt injectate in zǎcǎmant in scopul mentinerii presiunii zǎc., recuperǎrii secundare a petrolului sau inmagazinǎrii subterane a gazelor.

Legile gazelor

Constanta gazelor -R

Legea gazelor perfecte este definitǎ de relatia :

pV = n R_u T unde :

n = nr. de moli care se detrminǎ cu relatia ( n = )

R_u = constanta universalǎ a gazului

T = temperatura absolutǎ

p si V = presiunea si volumul gazului

In conditii normale de temperaturǎ si presiune (T - 273,15 K ; p = 1,01325 . 10⁵ Pa) ecuatia aplicatǎ unui Kmol de gaz ce are V = 22,414 m³ constanta universalǎ are valoarea :

R_u = 8314 J/Kmol .K

Nr de molecule dintr-un mol = 6,023 . 10²³ (Nr. lui Avogadro)

Pentru un gaz oarecare constanta lui se determinǎ cu relatia :

R = astfel pt. CH₄ R = ; pt C₂H₆ = 276 J/kg K

La temperaturi relativ mari si presiuni mici gazele se comportǎ aprox. ca gazele perfecte

La presiuni de distributie >> 6 bari Z = 1

La presiuni mai mari    Z > 1

Starea normalǎ a gazelor

a)     starea normalǎ fizicǎ la t = 0⁰C adica T = 273,15 si presiunea normalǎ p_N = 101325 N/m² sau Paascali , 1,01325 at , sau 760 mm coloanǎ Mercur

b)    starea normalǎ tehnicǎ la t = 20⁰C adica T = 293,15 si presiunea normalǎ p_N = 98066,5 N/m² sau Paascali , 0,980665 at , sau 735,5 mm coloanǎ Mercur

c)     starea standard la t = 15⁰C adica T = 288,15 si presiunea normalǎ p_N = 101325 N/m² sau Paascali , 1,01325 at , sau 760 mm coloanǎ Mercur

d)    volumul molar al gazului in conditii standard = 23,6503 m³/Kmol

Factorul de abatere - Z

Legea de stare a gazelor perfecte a fost extinsǎ pentru domeniul de stare a gazelor reale monocomponente sub forma :

p V = n Z R_universal T unde Z = factorul de abatere de la legea de stare a g. perfecte

Factorul Z poate fi exprimat ca Z = f (p_redusa , T_redusǎ) unde ;

p_redusǎ = ; V_redus = ; T_redusa =

Pentru :

Z < 1 volumul gazului este mai mic decat al gazului perfect

Z = 1 la aceeasi presiune gazul real este mai compresibil decat ce ideal

Z > 1 volumul gazului real este mai mare decat al g. perfect. Gazul real este mai expansibil

Factorul  Z  este mǎsura compresibilitǎtii gazului real fata de cel perfect

In cazul gazelor multicomponente se utilizeazǎ presiunea pseudoredusǎ si temperatura pseudoredusǎ definitǎ prin relatiile :

p_pseudoredusa = ; T_pseudoredusa = unde :

P_{pseudocritica} = ; T_{pseudocritica} = ; n_i = fractia molarǎ a comp. i

Densitatea si volumul specific al gazelor

Densitatea gazelor poate fi detarminatǎ din ec. de stare a gazelor reale in care n = Nr. de moli

n = 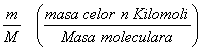iar si introducind inrelatia pV= n Z R_uT

se obtine 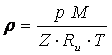ecuatia de calcul a densitǎtii unuio gaz monocomponent

Pt. gazele multicomponante se inlocuieste M cu M_m ( masa molecularǎ medie a amestecului)

M_m = M_i = masa molecularǎ a componentului i

n_i = concentartia molecularǎ a comp. i

Volumul specific al gazelor este dat de relatia

V_specific =

Densitatea relativǎ a gazelor care se utilizeazǎ cel mai frecvant se calculeazǎ cu relatia

unde 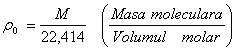_aer = 1,293 kg/m³

Facturul de volum al gazelor

Prin definitie factorul de volum este raportul dintre volumul fazei gazoase in conditii de zǎcǎm. rezultat dintr-un metru cub de gaze in conditii normale Deci :

b_g = si stiind cǎ :

V_{gaze zac.} = si V_g0 = atunci relatia de calcul a foctorului de vol.

b_g =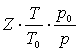

Compresivibilitatea gazelor

Aceastǎ proprietate se exprimǎ prin coeficientul de compresivibilitate

din ecuatia de stare a gazelo V =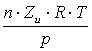

Factorul Z este functie de presiune si se poate scrie :

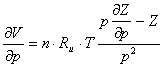introducand aceastǎ relatie in prima rezultǎ :

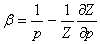unde ; (t)= la un anumit timp

Pentru CH₄ = se folosesc parametrii redusi

Pentru gaze multicomponente se folosesc parametrii pseudoredusi

Z_i = f(T_redusǎ ; P_redusa) ; Z_i = f(T_pseudoredusa , P_pseudoedusa)

Dupǎ o anumitǎ perioadǎ (t) se poate calcula Z^(t) care este mai mic decat initial si este functie de p^(t)

In literatura de specialitate sunt date variatiile coeficientului de compresibilitate functie de conditiile pseudoreduse care au un grad mai mare de eroare la temperaturi mai mici.

Vascozitatea gazelor naturale

Vascozitatea este asociatǎ fenomenului de curgere a fluidelor lichide , gazoase sau combinatii ale acestora. Vascozitatea este o mǎrime importantǎ a gazelor care face sa se deosebescǎ de gazul perfect unde lipsesc fortele de frecare internǎ intre particulele aflate in miscare

Vascozitatea sau frecarea internǎ este acea proprietate pe care o au fluidele reale de a opune rezistentǎ in cazul in care 2 straturi paralele se deplaseazǎ cu viteze diferite.

Vascozitatea gazelor depinde de compozitia lor , scade cu densitatea, creste cu presiunea si temperatura cu unele anomalii la presiuni mari.

Variatia vascozitatii dinamice in functie de temperaturǎ este datǎ de reletia lui Sutherland

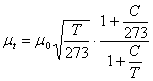unde :

_t = vaswcozitatea dinamicǎ la temperatura t ⁰C

= vaswcozitatea dinamicǎ la temperatura t₀ = 0 ⁰C

T = temperatura absolutǎ in K

C = Constanta lui Sutherland care are valori de 112 pt O₂ ,164 pt CH₄ , 225 pt C₂H₆ si 322 C₃H₆

Cand se cunoaste compozitia gazelor si vascozitatea componentilor acestuia la o anumitǎ temperaturǎ si presiune se poate calcula ascozitatea amestecului cu relatia :

y_i = concentratia molarǎ a fiecǎrui gaz si M= masa molecularǎ

Vascozitatea se poate calcula si cu ajutorul diagramelor.

Comportarea sistemelor de hidrocarburi in conditii de zǎcǎmant

In timpul exploatǎrii unui zǎcǎmant pot apǎrea diferite situatii . In ingineria de zǎcǎmant din punct de vedere al compozitiei se utilizeazǎ urrmǎtoarele notiuni :

a)     zǎcǎmant de gaze

b)    zǎcǎmant de gaze cu condensat

c)     zǎcǎmant de petrol

d)    zǎcǎmant de petrol si gaze

Fiecǎrui zǎcǎmint i se poate stabili o diagramǎ de comportare a zǎcǎmintului.

Compozitia fazelor gazoasǎ si lichidǎ variazǎ in timpul expolatǎrii datoritǎ presiunii de zǎcǎmint. A studia comportarea de stare de agregare a sistemelor de hidrocarburi inseamnǎ a stabili functie de variatia unui parametru de stare (presiunea) numǎrul si natura fazelor prezente, momentul in care in sistem apare o nouǎ fazǎ , momentul in care sistemul trece de la faza unicǎ la cea bifazicǎ si invers

In mod normal in urma unei expansiuni izoterme are loc vaporizarea .Fenomenul este specific comportǎrii normale.

In cazul unei anumite compozitii a sistemului de hidrocarburi si a unor temperaturi la care se gǎseste sistemul ca rezultat al expansiunii izoterme are loc condensarea vaporilor. Aceastǎ comportare se denumeste comportare anormalǎ sau retrogradǎ

Curba de comportare in exploatare a zǎcǎmintelor de gaze

100% faza lichida E

A Punctul critic

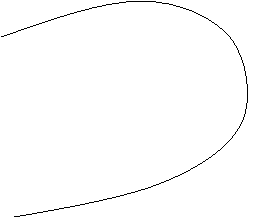P L C E₁ G

Punct cricondenterm

A₁

E₂

C_T

G

L + V

A₂ 100% fazǎ vapori

E₃ V

T

T_Z < T_CR < T_Z < T_CT < T_Z

Domeniul I Domenmiul II Domeniul III

Domeniile de existentǎ a comportǎrii normale si retrograde sunt delimitate de temperaturile ce pot fi intalnite in zǎcǎmant

Sunt utile urmǎtoarele precizǎri :

1)Punct triplu corespunde situatiei in care cele 3 faze ( S, L, G) se gǎsasc

impreunǎ in echilibru

2) Punct critic corespunde unei anumite valori a presiunii si temperaturii pentru

care faza lichidǎ si gazoasǎ coexistǎ

3) Punctul cricondenterm ( C_T) este punctul de temperaturǎ maximǎ la care faza gazoasǎ si

cea lichidǎ se aflǎ in echilibru.

4) Punctul cricondenbar (C_P) este punctul de presiune maximǎ la care faza gazoasǎ si cea

lichidǎ se aflǎ in echilibru.

5) Curbe de egal titlu sau curbǎ de egalǎ fractie de lichid este locul geometric al pct. de

coordonate ( P,T ) in care fractia volumetricǎ de lichid este const.

Fenomenul de trecere din gaz in lichd (condenseazǎ vapri la presiune scǎzutǎ ) se numesc zone de condensare retrogradǎ

Domeniul I - specific comportǎrii normale

Domeniul II - cind p > p_critic atunci sistemul initial se aflǎ in stare gazoasǎ

- cand p = p_critic atunci apare prima picǎturǎ de lichid

Domeniul in care ca rezultat al expansiunii izoterme apare condensarea ,este domeniul de comportare retrogradǎ ,cunoscut prin asa numita condensare anormalǎ sau retrogradǎ Acest domeniu se stabileste prin unirea punctului critic cu punctul cricondenterm prin punctele de tangenta ale dreptelor reprezentand expansiunea izotermǎ la diferite temperaturi , cu liniile de egalǎ concentratie in fazǎ lichidǎ sau vapori.

Domeniul III - comportarea sistemului este normalǎ . T_zacamint > T_{cricondenterm}

Ecuatiile fundamentele ale miscǎrii fluidelor in zǎcǎmintele de hidrocarburi

Sistemul de ecuatii fundamentale :

a)     ecuatia filtratiei sau ecuatia echilibrului dinamic

b)    ecuatia continuitǎtii sau ecuatia conservǎrii masei sau ecuatia de bilant material

c)     ecuatia de stare

d)    ecuatia bilantului de cǎldurǎ

Ecuaia linearǎ a filtratiei unui fluid monofazic

Dacǎ predominante sunt fortele de frecare, fortele de presiune si cele gravitationale in timp ce fortele de inertie sunt neglijabile ecuatia dinamicii fluidelor se numeste ecuatia linearǎ a filtratiei sau ec. lui Darcy. Experientele lui Darcy au dus la o relatie a debitului

q =

Se considerǎ cǎ t =ct , viscozitatea dinamicǎ a fluidului = ct, fluidul este incompresibil = ct si densitatea = ct. Apelind la ec. hidrostaticǎ si tinind cont de conditiile impuse se poate scrie cǎ : q = k Se stie cǎ atunci q =

Debitul unui fluid se poate scrie ca produsul intre viteza de filtratie si aria suprafetei astfel :

q = v A → v A = unde v = viteze de filtaratie

Ecuatia lui Darcy este ecuatia linearǎ a filtratiei si se poate scrie ;

v = - unde dp^* = presiunea redusǎ

Ecuatia lui Darcy raportatǎ la sistemul de axe carteziene se poate scrie :

v_x = - ; v_y = - ; v_z = - echivalente cu ecuatia

unde = operatorul lui Hamilton si este :

Raportul intre ( vascozitate dinamicǎ)

Graficul vitezei de filtratie in raport cu gradientul hidraulic este dat mai jos : i = dh/dx

a)     zona de repaus (zonǎ fǎrǎ miscare) - fortele electrostatice dintre fluid si particolele solide sunt mari si nu pot contracare gradientul termic

b)    zona preliminarǎ - moleculele de apǎ sunt puternic fixate de suprafata particulei datoritǎ fortelor electromoleculare . Aceasta reprezintǎ apa puternic legatǎ sau adsorbitǎ.

c)     zona linearǎ - ecuatia lui Darcy (fortele electromoleculare si cele de inertie sunt neglijabile in raport cu fortele gravitationale , de presiune si cele de frecare.

d)    zona postlinearǎ laminarǎ - corespunde intervalului in care miscarea fluidelor este incǎ linearǎ dar cresterea gradualǎ a fortelor de inertie determinǎ abaterea de la dreapta lui Darcy

e)     zona postlinearǎ turbulentǎ - o mare parte din gradientul hidraulic este disipat pt. invingerea fortelor de inertie

v

i₀

a b c d e i

i₀ i_i i_s

De regulǎ miscarea petrolului este in zona linearǎ (a lui Darcy), iar filtratia gazelor poate apare in ultimele 3 zone ale graficului din figura de sus.

Ecuatia nelinearǎ a filtratiei

Dacǎ fortele de inertie au acelasi ordin de mǎrime cu fortele de frecare, de presiune si eventual cu cele gravitationale , ecuatia dinamicii fluidelor intr-un mediu poros se numeste ecuatia nelinearǎ a filtratiei. Ea capǎtǎ forma :

unde a = Si b = iar

= coficientul de rezist. hidraulicǎ inertialǎ a mediului poros

In cazul filtratiei nestetionare a fluidelor ecuatia poate fi completatǎ :

coeficient determinat experimental.

Ecuatia continuitǎtii

In cazul in care ecuatia continuitǎtii sau ecuatia conservǎrii masei de fluid se aplicǎ unui domeniu infinitezimal ea se numeste ecuatia microscopicǎ a continuitǎii

In cazul in care volumul de control are dimensiuni finite ec. continuitǎtii se numeste ecuatia macroscopicǎ a continuitatii si se obtine prin integrarea ec. micrscopice a continuitǎtii pe volumul macroscopic considerat.

Considernd un domeniu de control macroscopic se poate scrie :

Q_{masic intrat} - Q_{masic iesit} + Q_{masic datorat surselor} unde :

dM = masa acumulatǎ in timp

Aceastǎ ecuatie este echivalentǎ cu ; M_intrat - M_iesit + M_surse = dM si considerand cǎ :

dM = M_{t + t} - M_t unde :

M_{t + t} = masa de fluid extrasǎ din zǎcǎmant si corespunzǎtoare unei anumite trepte de timp

M_t = masa de fluid existentǎ in zǎcǎmant in momentul initial

si cǎ M =ρ V ecuatia devine :

V_initial - V_esit + V_surse = V_{t+ t} - V_t

Prin dezvoltare se ajunge la relaii ce pot fi utilizate.

Ecuatiile de stare

Starea unui fluid pote fi caracterizatǎ printr-o reletie de forma

f ( p, ρ ,T ) = 0

Ecuatia se denumeste ca ecuatia de stare si se particulaizazǎ functie de tipul fluidului :

a ) pentru lichide incompresibile ( = = ct )

b) pentru lichide compresibile ( =

c) pentru fluide (gaze reale compresibile )

Modele zerodimensionale folosite in exploatarea zǎcǎmintelor de gaze

Modelele zerodimensionale sunt modele care au la bazǎ ecuatia macroscopicǎ a bilantului material . Parametrii zǎcǎmintului pot fi exprimati prin intermediul ecuatiei , utilizand valorile medii ponderate volumice. Prin folosirea parametrilor medii pondereti volumic , miscarea nu mai depinde de nici o variabilǎ spatialǎ Parametrii medii ponderati volumici sunt exprimati prin intermediul urmǎtoarelor relatii :

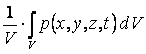
p_m = _m 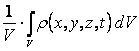; R_{soluti medie} =

b_m = unde ; b_mediu = factorul de volum mediu si R_m = ratia de solutie medie

Convertirea volumului de fluide produse in timpul exploatǎrii zǎcǎmantului in conditii de zǎcǎmant se realizeazǎ prin folosirea factoruluimde volum (b_m) si a ratiilor de solutie (R_m)

Zǎcǎminte cu frontiere impermeabile

Zǎc. din aceastǎ categorie produc gaze datoritǎ expansiunii lor realizanduse astfel regimul de depletare. Modelul zerodimensional pt, aceste zǎc. se scrie pornind de la ecuatia :

V_initial - V_esit + V_surse = V_{t+ t} - V_t si tinand cont de urmǎtoarele aspecte

a)     Volumul gazelor intrate = Volumul gazelor iesite = 0

b)    Volumul datorat surselor V_s = - G_p

c)     Volumul gazelor existente in zǎcǎmant la timpul (t + t) = cu volumul porilor saturati cu gaze in cazul neglijǎrii compresibilitǎtii apei interstitiale - volumul rezultat din destinderea elasticǎ a apei interstitiale si a rocii.

d)    Volumul gazelor din zǎcǎmant in momentul initial in conditii normale normale = rezerva geologicǎ = G.

La inceput existǎ un P_zacamint (P_z) si o temperaturǎ de zǎcǎm. (T_z) initialǎ . In frontierǎ nici nu intrǎ si nici nu iese fluid. Deci prin exploatare P_zacamint scade (regim de depletare).

Se poate scrie cǎ :

V_i - V_e + V_s = V_ramas ; V_ramas = V_{t + t} - V_t Tinand cont cǎ : V_intrat = V_iesit rezultǎ

V_{datorat surselor} = V_ramas

In realitate lucrurile nu stau chiar asa . Istoricul de productie si datele din mǎsurǎtori ne aratǎ cǎ nu existǎ un asemenea sistem . Intr-un astfel de zǎcǎmant apa de zǎcǎmant avanseazǎ pe structurǎ si duce lent la diminuarea suprafetei productive. Sondele marginale la un moment dat produc gaz si apǎ san numai apǎ.

Partea matemeticǎ pentru zǎcǎmintele cu frontiere impermeabile

S-a arǎtat cǎ ;

V_i - V_e + V_s = V_ramas si V_intrat = V_iesit = 0 atunci V_{datorat surselor} = V_ramas unde :

V_{datorat surselor} = productia de gaz

V_rǎmas = V_{t + t} - V_t si V_{t + t} = Volumul de gaze extrase din zǎc. corespunzǎtor unei anumite trepte de timp iar V_t = volumul de fluid existent in zǎcǎmant la momentul initial.

Volumul de pori saturati in fluid se calculeazǎ cu relatia :

V_psg = m V unde m = porozitatea si V = volumul de pori

Din acest volum de pori numai o parte sunt saturati cu gaz iar o altǎ parte cu apǎ interstitialǎ.

in laborator se calculeazǎ apa interstitialǎ pornind de la relatia

S_g + S_a = 1 Deci :

V m S_g = V m (1 - V_{a initial}) = [ V m (1 - S_{a initial}) - ( V m S_{a initial a} + m V _g p]

m = porozitatea mediului

V = volumul brut al zǎcǎmantului

S_{a i} = saturatia in apǎ interstitialǎ

_a si _g = coeficientul de compresibilitate a apei respectiv al porilor calculat cu _a

p = diferenta de persiune (intre p. initialǎ si p. medie ) unde : p_mediu =

b_g = factorul de volum al gazelor la presiune medie

Volumul gazelor in momentul initial este rezerva

G⁽ⁱ⁾ = V m S_g sau G = V m (1 - S_{a i})

Faptul cǎ V (volumul brut al zǎcǎmantului ) este greu de calculat atunci rezerva se estimeazǎ nu se calculeazǎ dupǎ relatia :

Apaland la relatia care dǎ coeficientul de volum in conditii initiale si in conditii medii astfel :

b_{g i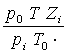} = si b_g = 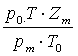si introducand in relatiile

rezultǎ 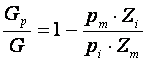Se stie cǎ

Inlocuind relatia devine :

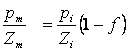
Se poate reprezenta grafic raportul functie de facorul de recuperare ( f )

istoric de productie

p₁

p₂^(t) _{Dupǎ o perioadǎ de timp acest punct devine istorie}

p₃^(t) partea de prognoza

f(r₁) f(r₂) f(r₃) f ; f = f(G,p)

Factorulm de recuperarae poate fi ameliorat prin utilizarea compresoarelor

Utilizarea unui numǎr de compresoare pt. extractie in primǎ fazǎ creste productia de gaze pentru un anumi timp si dupǎ aceea la o diminuare sau chiar o blocare a sondei datoritǎ cresterii vitezei de influx a gazelor din strat in sondǎ , ce duce la condensrea fazei de vapori din masa de gaz datoritǎ vitezelor mare de filtrare asociate cu valorile de temperaturǎ propice

Reprezentand grafic () functia de f(G) se poate face o estimare a rezervelor geologice la un moment dat.

Zǎcǎminta cu influx de apǎ

Se numesc si zǎcǎminte cu impingere de apǎ . Acestea sunt acelea pentru care zǎcǎmantul de apǎ compenseazǎ anumite volume. Ele sfarsesc prin inundarea lor in intregime. Modelarea influxului de apa se poate stǎpani foarte greu desi existǎ multe teorii in acest sens. Exploatarea lor duce la formarea de conuri de apǎ in zǎcǎmant. Sondele periferice inundate se mentin si pe ele se fac mǎsurǎtori pentru a vedea avansarea stratului de apǎ.

Modelul zerodimensional pentru astfel de zǎcaminte se poate obtine prin particularizarea relatiei

M_i - M_e + M_{datorat surselor} + M_{reactii chimice} + M_{transfer interfazic} = M_acumulatǎ si

V_i - V_e + V_s = V_{t + t} - V_t = V_ramas

Termenul care se scimbǎ este acela care defineste volumul de gaze existente in zǎcǎmant la timpul (t + t) . In acest caz

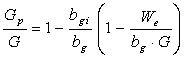dacǎ se exprimǎ b_{g i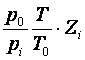} = si b_g =

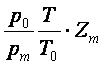
se obtine :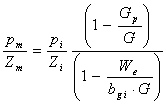

Intucat W_e este functie de timp dependenta lui () de nu mai este linearǎ ca in cazul zǎcǎmintelor cu frontiere impermeabile si este redatǎ mai jos :

a b c

d

- curba (a) corespunde unui acvifer de dimensiuni mici si comportrea lui se apropie de linear (d)

- curba (b) si (c) corespund unor zǎcǎminte de gaze asociate cu cate un acvifer mare

Atunci cand existǎ date suficiente de presiune si productie pe o perioedǎ relativ mare de exploatare se poate calcula " Rezerva geologicǎ aparentǎ "

G_aparenta =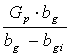

Dacǎ pentru diferite perechi de date [ G_p ; b_g(p_{m initial})] se obtin valori diferite atunci zǎcǎmantul este cu impingere de apǎ expresia de calcul a rezervei aparente devine functie de rezervǎ (G)

G = 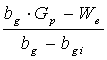G_a = G +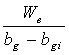

Cercetarea sondelor de gaze naturale

Cercetarea sondelor de gaze naturale constituie obiectul de activitate a ingineriei de zǎcǎmant. Aceasta stabileste pentru fiecare sonda retetele de productie , SNGN Romgaz are in functiune 1.700 sonde de gaze , fiecare cu specificul ei care trebuiesc monitorizate (cercetǎri parametriii de presiune si temperaturǎ in regim static si dinamic.) Acesti parametrii se pot mǎsura cu aparate deosebit de performante (manometre si termometre performante de ultimǎ generatie) Aparatura este capabilǎ prin intermediul unor ansamble sǎ introducǎ in sondǎ termometre si manometre cu cuart care pot inregistra presiunea si temperaturǎ dinsondǎ cu o exactitate mare si datele sunt descǎrcate pe calculator si apoi interpetate.

Procesele de cercetare au o importantǎ deosebitǎ in determinarea debitelor maxime admisibile, si a factorilor care limiteazǎ aceste debite , coeficientii de rezistentǎ la filtrarea gazelor spre zona productivǎ si de asemenea stabilirea debitelor potentiale ale sondelor,

Suportul teoretic al acestor metode de cercetare este dat de relatiile ce guverneazǎ miscarea fluidelor prin medii poroase . Ecuatiile componente ale acestui suport sunt :

a)     Ecuatia lui Darcy sau ecuatia filtratiei sau ecuatia echilibrului dinamic

b)    Ecuatia continuiotǎtii sau ec. conservǎrii masei sau ec. de bilant material

c)     Ecuatia de stare

d)    Ecuatia bilantului de cǎldurǎ (aplicabilǎ atunci cind tempreatura in zǎc. variazǎ in timpul exploatǎrii datoritǎ folosirii unor metode termice pentru imbunǎtǎtirea facorului de recuerare (mai ales le sondele de petrol)

Acest sistem de 4 ecuatii fundamentale permite sǎ aflǎmm variatia in timp si in spatiu a presiunii , vitezei ca mǎrime vectorialǎ , a masei specifice si a temperaturii.

Se disting cercetǎri ale sondelor in :

a)     regim stationar de miscare a gazelor

b)    regim nestationar de miscare a gazelor

Toate proiectele se fac in regim stationar de miscare a gazelor . Existǎ un regim nestationar de miscare la inchiderea si deschiderea sondelor cand parametrii se schimbǎ si sonda intrǎ in regim stationar. Cand sonda intrǎ in regim stationar sugestivǎ este reprezentarea unui model fizic de prezentare a miscǎrii gazelor.

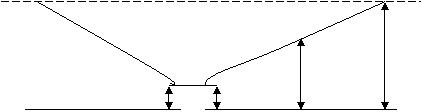
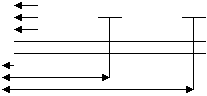
Studierea miscǎrii gazelor se face dupǎ un model fizic , in care miscarea gazelor cǎtre sondǎ este radial planǎ si simetricǎ

Ecuatia difuziei specificǎ acestui regim de curgere este datǎ de relatia

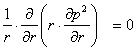
Solutia general a acestei ecuatii este datǎ de relatia :

(2) p² = a ln r + b

Solutia particularǎ a relatiei se poate obtine prin determinarea valorilor constantelor a si b asociate cu urmatoarele condiii r = r_s p = p_d r = r_contur p = p_zacamint unde ;

r_s si r_ct = sunt raza sondei respectiv raza conturului de alimentare

p_{s si} p_ct = presiunea din sondǎ, respectiv pe conturul de alimentare

Specific miscǎrii radial plane a gazelor este faptul cǎ sonda care dreneazǎ o zonǎ cilindricǎ de razǎ (r_s) , are frontiera (conturul ) complt deschis astfel incat pentru orice debit de productie constant productia cumulativǎ este integral compensatǎ de gazul ce intrǎ in raza de drenaj prin frontiera exterioarǎ

Altfel spus presiunea pe conturul de alimantare p_contur = ct , deci variatia

Q = ct

_{strat impermeabil} p p_ct

p_d p_d

h

r_s r r_ct

h = grosimea stratului productiv p_d = presiunea dinamicǎ a sondei

r_s = raza sondei p = pres. intre raza sondei si contur. de aliment.

r = raza curentǎ p_ct = pres. pe conturul de alimentare

r_ct = raza conturului de alimantare Q = debitul de gaz al sondei

Desi conditiile miscǎrii stationare nu sunt indeplinite niciodatǎ integral ele sunt frecvent acceptate gratie faptului cǎ operatiile de productie sunt proiectate la debite constante periodic.

Particularizand relatia (2) pentru conditiile [r = r_s p = p_d r = r_contur p = p_zacamint ] se poate determina valorile lui (a) si (b) astfel :

p_d² = a ln r_s + b si p_ct² = a ln r_ct + b explicitand (a) si (b) se obtine

a = si b =

Inlocuind aceste constante in ecuatia generalǎ se obtine :

p² =

Din relatie se vede cǎ presiunea variazǎ dupǎ o curbǎ logaritmicǎ iar curbele izobare sunt cercuri concentrice cu sonda.

Vitaza de filtratie - se face prin utilizarea relatiei lui Darcy . Se stie cǎ vitaza de filtratie se calculeazǎ cu relatia v = 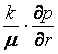iar unde ;

k = permeabilitatea mediului si = viscozitatea dinamicǎ a fluidului

deci se poate scrie vitaza de filtratie :

v =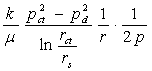

Stiind viteza de filtratie se poate calcula debitul cu relatia :

Q = v A_c unde A_c = 2 r h ( sectiunea vie de curgere a g. prin mediul poros )

Introducand in formula debitului viteza de fltrare se determinǎ debitul cu relatia ;

Q =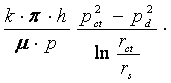

Debitu volumetric in conditii normale se poate calcula cu relatia :

Q₀ =

Din relatie se vede cǎ debitul de fluid variazǎ direct proportional cu produsul (k h) care reprezintǎ capacitatea de curgere a stratului

Asa cum s-a afirmat studiul cercetǎrii zǎcǎmintelor este acela de a determina unii parametrii hidrodinamici cum ar fi presiunea , debitul si vitaeza de filtratie a gazelor.

Dar pe lingǎ parametrii hidrodinamici amintiti sunt f. importanti si parametrii adiacenti cum ar fi :

a)     permeabilitatea efectivǎ a fluidelor

b)    capacitatea de curgere a stratului

c)     indicela de productivitate

d)    coeficientul de noninertie ( Non - Darcy)

In foarte multe cazuri permeabilitatea stratului din jurul sondei este mai redus decit in intreaga zonǎ de influientǎ ca urmare a efectelor traversǎrii stratului productiv prin foraj . Efectul de reducere a permeabilitǎtii in jurul sondei se poate asimila cu o cǎdere de presiune suplimentarǎ cu efecte directe asupra debitului de productie. Dacǎ se noteazǎ cu p_suplimentra aceastǎ cǎdere de presiune ea se calculeazǎ cu relatia :

Cǎderea suplimentarǎ de presiune se noteazǎ cu S si se denumeste ca factor de skin . Aceste este o mǎrime adimensionalǎ (din zona de permeabilitate modificatǎ) si se calculeazǎ astfel :

S = 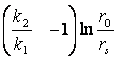unde :

k₁ = permeabilitatea aferentǎ mediului poros de razǎ (r₀) (permeabilitate modificatǎ)

k₂ = permeabilitatea nemodificatǎ a mediului poros (permeabilitate originalǎ)

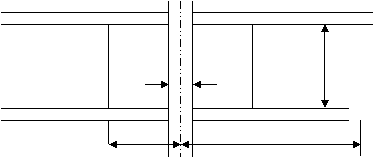
k₂ k₁ k₁ k₂

2r₀ k₂ k₁ k₁ k₂

r₀ r_ct r_fisura 10 m

Valorile pozitive ale lui S existenta in jurul sondei a unei zone de permeabilitate micsoratǎ

Valorile negative ale lui S existenta in jurul sondei a unei zone de permeabilitate mǎritǎ

Factorul de skin influenteazǎ debitul. In formula de calcul a debitului factorul de skin intrǎ la numitor. Deci pentru a mǎri debitul trebuie ca factorul de skin sǎ fie cat mai mic.

Ecuatia in doi termeni

Rezultatele cercetǎrii sondelor de gaze pot fi prelucrate cu ajutorul ecuatiei caracteristice de curgere denumitǎ si ecutia in doi termeni de forma :

p²_ct - p²_d = AQ + BQ² unde ;

A si B sunt coeficienti de rezistentǎ la filtrarea gazelor prin mediul poros permeabil

Determinarea acestor coeficienti se face fie grafic fie pe cale analiticǎ . Dupǎ determinarea acestora se pot determina si ceilalti parametrii aferenti mediului poros.

Reprezentarea graficǎ a ecuatiei implicǎ intii transpunerea ei intr-o formǎ linearǎ asfel ;

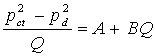
Diagrama care se obtine se denumeste Diagrama indicatoare liniarizatǎ in cazul miscǎrii nelineare a gazelor

B= tg

A

Q m³ /zi

Prin determinarea coeficientilor de rezistentǎ la filtrarea fluidului prin mediu permeabil A si B se pot stabili unii parametrii semnificativi ai mediului poros cum ar fi :

a)     raza de influientǎ a sondei in perioada cercetǎrii

b)    capacitatea de curgere a stratului

c)     coeficientul de inertie (Non Darcy)

d)    indicele de productivitate

e)     debitul potential al stratului

f)      facorul de skin

Parametrii care ne aratǎ cat de corect functioneazǎ sondele sunt parametrii in regim stationar.

Investigarea sondelor in regim nestationar

Miscarea nestationarǎ a fluidelor prin medii poroase este caracterizatǎ prin variatia in timp a parametrilor hidrodinamici In filtrarea nestationarǎ debitul de fluid intrat intr-un element de volum este diferit de cel care iese din acel element

Ecuatia diferentialǎ care defineste filtratia nestationare a fluidelor este ecuatia difuziei care este exprimabilǎ prin urmǎtoarele variante :

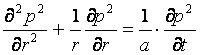ec. valabilǎ panǎ la 140 bar si a = 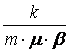si

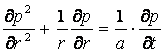ec. se aplicǎ peste presiuni > 200 bar

Ecuatia (1) estevalabilǎ in domeniul presiunilor mici cand produsul ( ) este constant iar ecuatia (2) este valabilǎ pentru presiuni mai marei de 200 bar cand produsul () = ct.

Metodele de cercetare a sondelor in cazul filtratiei nestationare sunt diverse .O clasificare a lor ar fi functie de felul cum sunt prelevate datele de investigare .

Dacǎ aceste date sunt prelevate prin inchiderea sau prin deschiderea sondelor metodele de investigare se nominalizeazǎ corespunzǎtor. Utilizarea unui grup de metode, sau a ambelor metode depinde de nivelul energetic al formatiunii cercetate precum si de performantele aparaturii folosite pentru investigare.

a) cercetarea orizonturilor de productie prin inchiderea lor

Se urmǎreste cercetarea parametrilor hidrodinamici ai orizonturilor de productie cum ar fi :

a)     capacitatea de curgere

b)    permeabilitatea efectivǎ

c)     coeficientul de difuzie hidraulicǎ

d)    mobilitatea fazelor

e)     porozitatea

f)      presiunea staticǎ

Specific acestui tip de cercetare este cǎ o sondǎ este in productie un interval de timp suficient ca in jurul zonei de influx strat - sondǎ distributia de presiune sǎ fie uniformǎ iar apoi sonda se inchide pentru refacerea presiunii statice.

Mǎsurǎtorile de presiune ua drept scop stabilirea caracteristicilor si a conditiilor fizice ale zǎcǎmantului Reprezentarea graficǎ a cacestui tip de cercetare este datǎ de graficele de jos

Q

Q

p_i ²

Q=0 i

t

t t +

Q

t

t    t + 10² 10 Variatia debitului si a presunii in contextul cercetǎrii Curba de refacere a presiunii aferenta unei

orizonturilor pri inchiderea lor sonde de gaze

Pe portiunea dreaptǎ a curbei se poate determina panta dreptei care se noteazǎ ci ( i )

Prin intermediul pantei se pot determina si ceilalti parametrii mentionati la punctele a - f totul functie de panta ( i )

Dintre acestia semnificativǎ este expresia explicitǎ a factorului de skin pentru filtrarea in regim nestationar care poate fi calculat spre deosebire de filtratia in regim stationar cand determinarea efectivǎ a factorului de skin este incertǎ. Factorul de skin se calculeazǎ cu relatia :

S = 1,151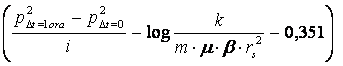

Relatia este valabilǎ dacǎ se ia ca bazǎ valoarea presiunii dupǎ 1 0rǎ de la inchiderea sondei

In ce priveste valoare lui (vascozitatea dinamicǎ ) si (factorul de compresibilitate ) ce intrǎ in calculul factorului de skin panǎ la 140 influenta lor nu este semnificativǎ . Peste acest nivel (140 bar) se recomandǎ a se face corectia lor in functie de presiune.

b)Cercetarea formatiunilor productive de gaze naturale prin deschiderea lor

Prin aceastǎ metodǎ de cercetare se inregistreazǎ variatia presiunii dinamice de adancime.

Variatia in timp a debituluisi a presiunii la deschiderea unei sonde este prezentatǎ grafic mai jos

Q

Q = 0

t

p p_statica

p_dinamicǎ

t

Curbele de stabilizare a presiunii dinamice se folosesc pentru determinarea parametrilor hidrodinamici caracteristici formatiunilor productive.

Reprezentarea graficǎ a p_d² = f(log t) pentru conditii reale de unde se pote determina panta ( i ) este redatǎ in graficul de mai jos..

10^-1 1 10 10² t (ore)

p_d²

i

-1 0 1 log t

Factorul de skin pentru acest tip de cercetare se calculeazǎ cu relatia :

S = 1,151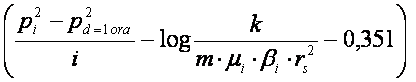

indicele i sereferǎ la conditiile initiale

Cercetarea orizonturilor productive prin deschiderea sondelor se poate aplica in diferite scopuri 

a)     aparitia de noi sonde

b)    evaluarea performantei zǎcǎmantului pentru stabilirea comportǎrii ulterioare

c)Cerceterea orizonturilor productive de gaze prin metoda izocronalǎ

Testarea izocronalǎ a orizonturilor productive este o metodǎ complexǎ de investigare si constǎ din alternarea la timpi egali a inchiderii respectiv a deschiderii sondelor.

Obtinerea de rezultate concludente este conditionatǎ si de inchiderea sondelor aferente orizontului respectiv si urmarirea in timp a tresiunii statice de adincime.

Aceste mǎsurǎtori se fac simultam pe mai multe sonde de pe acelasi orizont

Metoda de testare izocronalǎ , denumitǎ si metoda timpului egal de inchidere si deschidere a sondei are avantajul cǎ poate oferi informatii rapide de felul cum evoluiazǎ zǎcǎmintale depletive.

Un posibil test izocronal implicǎ urmǎtoarele faze :

a)     inchiderea tuturor sondelor de pe orizontul respectiv in vederea refacerii presiunii statice

b)    mǎsurarea presiunii statice prin intermediul manometrelor de adacime la 1 sau mai multe

c)     producerea sondei care are montat manometrul de adancime un anumit interval de timp

d)    consemnarea presiunilor dinamice de la capul de erupie si a debitului de gaze

e)     inchiderea sondei un anumit interval de timp si consemnarea valorilor de presiune

Reperzentarea graficǎ a evolutiei in timp a presiunii si a debitelor de gaz la testerea izocronalǎ este redatǎ in graficul de mai jos :

p

bar

t (ore)

Q

(m³/24 ore)

Q₁= ct    Q₂ = ct

Q = 0 Q = 0

t ( ore)

Q₂ > Q₁

Din datele inregistrate o sondǎ are comportare normalǎ atunci cand intre graficele care traduc variatia presiunii pe cateva cicluri de inchidere deschidere existǎ o similitudine acceptabilǎ

Aparitia unor decalaje intre grafice reprezintǎ indicii fie legate de dimensionrea incorectǎ a treptelor fie cǎ in zona de influx strat - sondǎ existǎ cǎderi suplimentare de presiune.