SISTEME DE COORDONATE: GEOGRAFICE (LONGITUDINEA, LATITUDINEA)

SISTEME DE COORDONATE

Coordonatele unui punct reprezinta parametrii ce caracterizeaza pozitia acestuia fata de un sistem de referinta ales. Sistemul de referinta este un sistem de plane, axe, curbe, etc. ce serveste ca reper fata de care se pozitioneaza puncte.

Pozitia punctelor fata de sistemul de referinta se determina prin distanta la planele (sau axele) sistemului ori prin distanta la origine si unghiul fata de o axa. Acesti parametri (distante, unghiuri, etc.) constituie coordonatele punctului.

Ca sistem de coordonate pentru pozitionarea pe sfera terestra a navei, a reperelor si pericolelor de navigatie, etc. s-a ales sistemul de coordonate sferice, (avand in vedere forma sferica a modelului matematic al Pamantului acceptat in navigatie). Pentru studiul problemelor de cartografie matematica si in general al problemelor de geodezie si hidrografie se utilizeaza alte sisteme (sistemul de coordonate rectangulare plane, geocentrice ecuatoriale, geodezice, etc.)

1. SISTEMUL DE COORDONATE GEOGRAFICE

Sistemul de coordonate geografice este sistemul utilizat in general in navigatie, pentru pozitionarea diferitelor puncte de interes pe sfera terestra.

Sistemul de referinta este format din doua plane perpendiculare, si anume:

planul ecuatorului;

planul meridianului Greenwich.

Urmele lasate de aceste doua plane pe sfera terestra sunt:

ecuatorul;

meridianul Greenwich.

Diversele puncte de interes se vor pozitiona fata de aceste doua cercuri mari care reprezinta in fapt axele sistemului de referinta al sistemului de coordonate geografice.

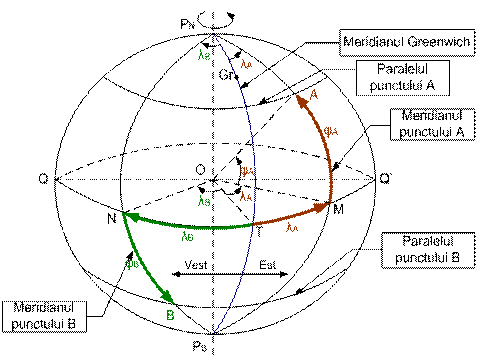
Pozitia unui punct oarecare de pe suprafata sferei terestre se va defini prin doua coordonate (j l), numite coordonate geografice, definite astfel (fig.9

LATITUDINEA GEOGRAFICA j a punctului A este arcul de meridian (sau unghiul la centrul sferei corespunzator), masurat de la ecuator pana la paralelul locului. Latitudinea geografica se masoara in unitati de arc sexagesimale, si ia valori de la 000(cand punctul A este situat pe ecuator) la 090(cand punctul A este situat in unul din polii geografici).

Cand punctul A se afla in emisfera nordica, valorii latitudinii geografice a acestuia i se atribuie conventional semnul algebric +, iar cand acesta se afla in emisfera sudica terestra, semnul algebric - .

In consecinta latitudinea geografica se exprima precizand numele emisferei (N sau S) sau precizand semnul algebric corespunzator (+ sau -). In navigatie, precizia de determinare a latitudinii geografice este de zecime de minut de arc. Deci :

[Fig.9] Coordonate geografice.

LONGITUDINEA GEOGRAFICA (l a punctului M este arcul de ecuator (sau unghiul la centrul sferei corespunzator), masurat de la meridianul Greenwich pana la meridianul locului. Se masoara in unitati de arc sexagesimale si ia valori de la 000 (cand punctul se afla pe meridianul Greenwich) pana la 180 (cand punctul se gaseste pe antimeridianul Greenwich).

Pentru punctele situate in emisfera estica, longitudinii acestora i se atribuie conventional semnul +, iar pentru puncte situate in emisfera vestica, semnul -. Longitudinea geografica a unui punct se exprima deci precizand numele emisferei terestre in care acesta se gaseste (E sau W) sau precizand semnul algebric (+ sau -). Valoarea longitudinii se exprima la o precizie de zecime de minut. Deci :

Se observa ca atat latitudinea cat si longitudinea sunt arce de cerc orientate.

In concluzie, coordonatele geografice caracterizeaza pozitia verticalei punctului fata de planul ecuatorului si fata de planul meridianului Greenwich.

In situatiile in care coordonatele geografice sunt folosite ca elemente de calcul, se recomanda sa fie notate cu semnele lor algebrice (+ sau -) si nu cu sensurile de contare (N, S, E, W), pentru a usura efectuarea operatiunilor.

2. POZITIILE RECIPROCE A DOUA PUNCTE PE SFERA TERESTRA. DIFERENTE DE COORDONATE GEOGRAFICE

In practica navigatiei, pe langa determinarea pozitiei unui punct izolat pe sfera terestra, apare necesitatea determinarii pozitiilor reciproce a mai multor puncte. Din acest motiv a aparut ca necesara introducerea notiunii de diferente de coordonate geografice. De asemenea, deplasarea navei pe sfera terestra presupune modificarea permanenta a coordonatelor sale geografice; pentru a preciza la un moment dat pozitia navei fata de punctul initial (ale carui coordonate se presupun a fi cunoscute), este necesara introducerea si utilizarea notiunii de diferente de coordonate geografice.

Pozitiile reciproce a doua puncte pe sfera terestra se determina cu ajutorul diferentelor lor de coordonate: diferenta de latitudine si diferenta de longitudine.

Sa consideram ca o nava merge de-a lungul meridianului locului, din punctul de plecare A (fig. 10) pana in punctul de sosire B; se observa ca longitudinea ramane neschimbata pe tot parcursul, latitudinea insa se schimba. Latitudinea punctului B este diferita de cea a punctului A cu o cantitate egala cu masura arcului AB = <AOB, care poarta denumirea de diferenta de latitudine.

[Fig.10] Diferenta de latitudine

DIFERENTA DE LATITUDINE (Dj dintre punctele A si B (unde punctul A este considerat punct de plecare sau punct initial, iar punctul B este considerat punct de aterizare sau punct final) este arcul de meridian (sau unghiul la centrul sferei corespunzator) masurat de la paralelul punctului de plecare (A) pana la paralelul punctului de sosire (B).

Diferenta de latitudine este deci un arc de meridian orientat.

Diferenta de latitudine primeste conventional semnul algebric (+), atunci cand orientarea vectorului AB este nordica si invers, se considera a fi negativa si va primi semnul (-) cand orientarea vectorului AB este sudica. Cu alte cuvinte, va fi pozitiva cand nava se deplaseaza catre nord, si negativa cand nava se deplaseaza catre sud.

Diferenta de latitudine ia valori de la 000 (cand nava se deplaseaza de-a lungul unui paralel) pana la 180 (cand punctele A si B se gasesc in cei doi poli terestri), si se exprima in grade, minute si zecimi de minut. Exemplu :

Dj=jB - jA

Cunoscand coordonatele geografice ale punctelor A si B, diferenta de latitudine dintre ele se va calcula cu relatia:

(5)

Relatia este valabila si pentru cazul in care A si B se gasesc in emisfere diferite (nava trece din emisfera sudica in emisfera nordica, ori invers).

In practica, diferenta de latitudine se va calcula dupa urmatorul tip de calcul :

Exemplu: O nava pleaca de la ancora din punctul A (j_A = 041 25'.₅ N si aterizeaza in punctul B ( j _B = 04655'.₂ N). Sa se calculeze diferenta de latitudine.

1) Calculul Dj

j_B

-j_A

Dj

DIFERENTA DE LONGITUDINE (Dl dintre punctele A si B, unde A este punct de plecare sau punct initial, iar B este punct de aterizare sau punct final, este arcul de ecuator (sau unghiul la centrul sferei corespunzator), masurat de la meridianul punctului A pana la meridianul punctului B.

[Fig.11] Diferenta de longitudine

Diferenta de longitudine este deci un arc de ecuator orientat. Astfel, Dl se considera a fi pozitiva si primeste semnul algebric + daca orientarea vectorului AB este estica, sau negativa, si va primi semnul algebric -, daca orientarea vectorului AB este vestica. Cu alte cuvinte, Dl este pozitiva cand nava se deplaseaza in sensul rotatiei Pamantului si negativa cand nava se deplaseaza in sens opus sensului rotatiei Pamantului.

Diferenta de longitudine ia valori de la 000 (cand nava se deplaseaza pe acelasi meridian) pana la 180 (cand punctul B se gaseste pe antimeridianul punctului A). Diferenta de longitudine se masoara in grade, minute si zecimi de minut :

Cunoscand coordonatele geografice ale punctului de plecare A si ale punctului de sosire B, diferenta de longitudine dintre cele doua puncte se calculeaza cu relatia algebrica:

Dl l_B l_A

In practica, diferenta de longitudine se va calcula utilizand urmatorul tip de calcul:

Exemplu: O nava pleaca de la ancora din punctul A (l_A = 03435'.₂E) si aterizeaza in punctul B (l_B=04144'_.1 E). Se cere sa se calculeze Dl .

Calculul Dl

l _B = +04144'.1

- l_A

Dl

Relatia si tipul de calcul sunt valabile pentru toate situatiile, mai putin cazul trecerii navei din emisfera estica in cea vestica (ori invers) prin intersectarea meridianului de 180⁰

In aceasta situatie, aplicand relatia de calcul, rezultatul va fi intotdeauna mai mare decat 180, si ca urmare, rezultatul final se scade din 360 , si i se schimba semnul.

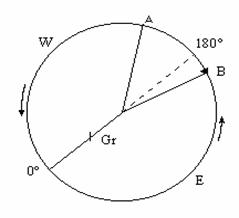
[Fig.12 ] Stabilirea semnului lui Dl

Se va analiza cazul trecerii navei dintr-o emisfera in alta prin intersectarea antimeridianului Greenwich (Fig.12) pe un exemplu practic :

Exemplu: Nava pleaca de la ancora din punctul A ( j_A=00538'.₇N _, l_A=17725'.₈W) si aterizeaza in punctul B (j_B = 00312'.₄ S ,l_B=17529'.₄E). Sa se calculeze diferentele de coordonate geografice dintre punctele A si B.

Rezolvare

1) Calculul Dj 2) Calculul Dl

j _B = -00312'.₄    l _B

j_A - l_A

Dj Dl

Dl

Dl

Pentru verificarea semnului obtinut din calculul algebric, se compara sensul de deplasare a navei ( vectorul AB) cu sensul de rotatie a sferei terestre in jurul axei proprii (sensul direct). Daca cele doua sensuri coincid, atunci semnul lui Dl este +, iar daca sensurile sunt opuse, atunci Dl va avea semnul - .

In cazul analizat, sensul de deplasare a navei se opune sensului de rotatie a sferei terestre in jurul axei proprii, deci semnul lui Dl este minus.