Sisteme de altitudini

Exista un numar relativ mare de sisteme de altitudini, dintre care se vor mentiona in continuare cele mai cunoscute.

La un sistem de altitudini, trebuiesc definite:

Ø      suprafata de referinta;

Ø      definitia cotei (altitudinii) in sistemul respectiv;

Ø      transformarea diferentei de nivel masurate prin nivelment geometric (care este unica) in sistemul de altitudini considerat.

1. Numere geopotentiale. Notam cu 0 punctul initial (fundamental) in reteaua de nivelment de la care porneste o linie de nivelment spre punctul P in lungul careia s-au masurat atat diferente de nivel cat si acceleratiile gravitatii. Din formula fundamentala se obtine:

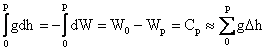(2.96)

Diferenta C_P intre potentialul geoidului W₀ si potentialul suprafetei de nivel W_P a punctului P este denumita numarul geopotential al punctului P, notiune introdusa in anul 1955 in cadrul AIG.

Concluzii:

Ø      Numarul geopotential caracterizeaza, in mod natural, o suprafata de nivel, fiind acelasi pentru toate punctele situate pe aceeasi suprafata.

(2.97)

Ø      Numarul geopotential se poate determina prin efectuarea celor doua tipuri de lucrari:

lucrari gravimetrice (g);

lucrari de nivelment geometric (Dh).

2. Altitudinea dinamica. Notiunea de altitudine dinamica a fost introdusa de Helmert in anul 1873. Daca ne referim insa la numarul geopotential C_P, altitudinea dinamica notata H^d se obtine prin impartirea numarului geopotential cu o valoare constanta si anume cu valoarea gravitatii normale, la altitudinea de 45 , raportata la alipsoidul de referinta:

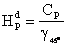(2.98)

Din punct de vedere dimensional altitudinile dinamice sunt exprimate in metri, insa ele nu au o semnificatie geometrica. Astfel, altitudinea dinamica a unui punct nu poate fi reprezentata ca o distanta de la o anumita suprafata la punctul considerat. Aceste altitudini pastreaza, in continuare, semnificatia fizica generata de impartirea numerelor geopotentiale cu o constanta aleasa in mod conventional.

Sistemul de altitudini dinamice este caracterizat printr-o proprietate deosebita si anume: punctele situate pe o anumita suprafata de nivel au aceeasi altitudine dinamica.

Referitor la nota de la inceputul paragrafului se mentioneaza:

Ø      suprafata de referinta este geoidul    cu potentialul (cunoscut) W₀;

Ø      altitudinea dinamica a punctului P () este definita cu relatia (2.89), unde: g este gravitatea normala la nivelul elipsoidului la latitudinea B = 45 g = 980617,6 mgali.

Ø      Corectia dinamica:

Pentru doua puncte A si B diferenta de altitudini dinamice poate fi scrisa sub forma:

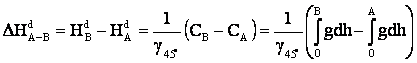(2.99)

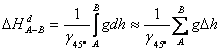(2.100)

Se poate transforma aceasta relatie in continuare:

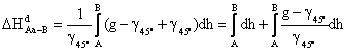(2.101)

astfel incat:

(2.102)

unde diferenta de nivel masurata:

Marimea este corectia dinamica pe traseul AB:

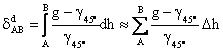(2.104)

Sistemul de cote dinamice a stat la baza crearii retelei de nivelment din Europa de Vest (Rseau Europen Unifi de Nivelment, prescurtat REUN).

3. Altitudinea ortometrica. Definitia altitudinii ortometrice este:

unde reprezinta media valorilor gravitatii in lungul liniei de forta P₀P atunci cand se are in vedere un numar infinit de segmente.

Deoarece marimea este imposibil de determinat practic, sistemul de altitudini ortometrice este un sistem de altitudini ideal, de referinta.

Diferenta de nivel in sistemul de altitudini ortometrice se calculeaza cu relatia:

(2.106)

unde reprezinta corectia ortometrica pe traseul AB:

(2.107)

4. Altitudinea Helmert. Valoarea medie , din relatia (2.105), prin care se defineste altitudinea ortometrica in functie de numarul geopotential, nu poate fi determinata practic, in mod riguros. De aceea, in locul acestei marimi s-au introdus alte valori, in functie de anumite ipoteze, rezultand diverse sisteme de altitudini.

Gradientul    gravitatii in interiorul Pamantului este o marime de extrem de variabila, practice din punct in punct. Ca o marime medie se poate considera . Rezulta ca graviatatea medie, notata , intre valoarea in punctual de masurare P(g) si in punctul redes pegeoid P(g₀) se poate determina cu formula:

(2.78)

Altitudinea Helmert poate fi scrisa sub forma:

(2.108)

Aceasta relatie a fost dedusa de Helmert in anul 1890 si de aceea altitudinile corespondente poarta numele sau.

5. Altitudinea ortometrica sferoidica. Sistemul de altitudini sferoidice a fost unul dintre cele mai folosite sisteme in etapa de dezvoltare a geodeziei in oricare tara, cand nu se dispunea de masuratori gravimetrice. Daca in relatia (2.107) se introduce g º g, se obtine expresia corectiei ortometrice sferoidice:

(2.109)

Formula de calcul practic a corectiei ortometrice sferoidice, folosita si in tara noastra in trecut, precum si in multe alte tari din Europa s-a dedus prin considerarea neparalelismului normal al suprafetelor de nivel (si in care caz este valabila aproximatia mentionata g º g). Astfel, pentru trasee de nivelment care merg dinspre sud spre nord, rezulta din (2.105):

(2.110)

Pentru calculul practic in tara noastra s-au considerat tronsoane in lungime de 1 km (ceea ce corespunde, aproximativ, pentru DB = ) obtinandu-se:

(2.111)

unde

(2.112)

Acest coeficient poate fi extras si din tabelele publicate de prof. M. Botez (1969), pg. 164 (pentru f^* s-a considerat valoarea 0,0053) in functie de latitudinea medie B_m.

6. Altitudini normale. In tara noastra este folosit, in prezent, ca sistem oficial de altitudini, sistemul de altitudini normale, fondat teoretic de M.S. Molodenski in anul 1945.

Plecand de la dificultatile reale pe care le prezinta utilizarea altitudinilor ortometrice, dintre care cunoasterea gravitatii medii in lungul liniei de forta reprezinta impedimentul principal, Molodenski propune ca in locul campului gravitatii sa se utilizeze campul gravitatii normale.

Acceptand aceasta ipoteza, formulele de calcul se pot determina prin utilizarea formulelor corespondente de la sistemul de altitudini ortometrice. Astfel, definitia altitudinii normale a punctului P, notata , este:

(2.113)

unde valoarea medie a acceleratiei normale a gravitatii in lungul normalei la elipsoid se calculeaza riguros cu relatia:

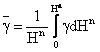(2.114)

Corectia in sistemul de altitudini normale se determina cu:

(2.115)

sau

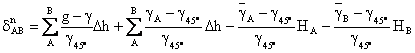(2.116)

Comparand relatiile (2.109) si (2.116) rezulta:

(2.117)

Aceasta relatie exprima legatura care exista intre corectiile normale si corectiile ortometrice sferoidice, punand in evidenta posibilitatea de trecere de la un sistem la altul, in cazul in care se cunosc anomaliile gravitatii pe traseul considerat. Corectia normala apare astfel ca formata din doi termeni principali:

Ø      corectia     datorata anomaliilor gravitatii;

Ø      corectia datorata neparalelismului suprafetelor de nivel (in conceptia ortometrica sferoidica).

Introducerea notiunii de sistem normal a condus si la necesitatea schimbarii suprafetei de referinta, in speta a geoidului, folosit in sistemul ortometric.

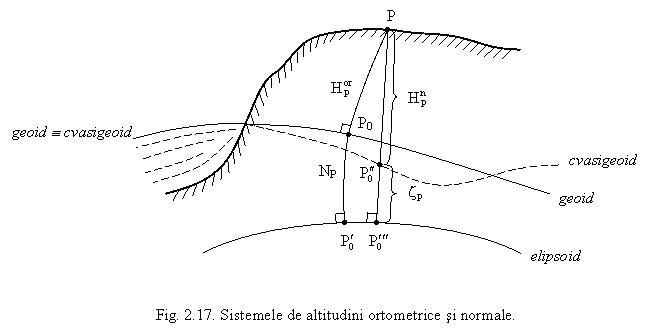
Pentru a intelege mai usor caracterul suprafetei de referinta in cazul sistemului normal, ne bazam pe altitudinile elipsoidice H^e, definite in raport de elipsod, in cele doua sisteme de altitudini avute in vedere (Fig. 2.17):

(2.118)

Cu N se noteaza ondulatiile geoidului, care sunt specifice utilizarii sistemului de altitudini ortometrice, iar cu z perturbatiile sau anomaliile altitudinilor.

Se presupune o suprafata astfel construita (Fig. 2.17), incat segmentul de normala la elipsoid sa fie egal cu z in orice punct in care se cunoaste aceasta cantitate. M.S. Molodenski a denumit aceasta suprafata cvasigeoid. Pe suprafete acvatice intinse (mari, oceane) cvasigeoidul coincide cu geoidul, sub continente existand diferente care depind de structura interna a Pamantului.

Pentru reperi de nivelment apropiati, situati la 1 - 3 km, pe un traseu de la sud spre nord, se poate aplica si urmatoarea formula:

(2.119)

unde Dh_AB este diferenta de nivel masurata;

g_m - valoarea acceleratiei gravitatii normale, calculata pentru media latitudinilor B_med si la cota medie H_med a celor doi reperi;

(g - g)_m - valoarea medie a anomaliilor acceleratiei greutatii, corespunzatoare celor doi reperi.