| CATEGORII DOCUMENTE |
| Demografie | Ecologie mediu | Geologie | Hidrologie | Meteorologie |
1. Suprafete de nivel, geoidul, linii de forta Relatia cunoscuta:
![]() (2.55)
(2.55)
unde s este o directie oarecare poate fi particularizata si pentru axele de coordonate, rezultand:
![]()
![]()
![]() (2.80)
(2.80)
Daca se considera o directie ![]() oarecare, astfel imcat sa se respecte
urmatoarea ecuatie
oarecare, astfel imcat sa se respecte
urmatoarea ecuatie
![]()
adica, daca se are in vedere o directie ![]() perpendiculara pe directia gravitatii g, rezulta:
perpendiculara pe directia gravitatii g, rezulta:
dW = 0 (2.82)
sau
W (x, y, z) = constant = c. (2.83)
Aceasta expresie reprezinta ecuatia unor suprafete echipotentiale, denumite de catre Laplace, suparafete de nivel. Rezulta ca suprafetele de nivel sunt perpendiculare, in oricare din punctele lor, pe directia gravitatii. Datorita structurii interne a Pamantului aceste suprafete sunt foarte complexe, cu multe ondulatii, fara muchii sau varfuri.
Schimbandu-se valoarea constantei c din relatia (2.83) se obtin diverse suprafete de nivel. Dintre suprafetele de nivel posibile, pentru geodezie o importanta deosebita o are suprafata de nivel zero, denumita geoid, notiune introdusa de catre Listing in anul 1873. Aceasta suprafata echipotentiala a fost propusa de catre Gauss ca figura matematica a Pamantului:
W (x, y, z) = W0 = constant. (2.84)
AIG recomanda in anul 1980:
W0 = (6263686 3) 10 m2s-2 (2.85)
Fiind in permanenta perpendicular pe directia gravitatii, geoidul are o configuratie foarte complexa. Modificarile de densitate din interiorul Pamantului conduc la schimbarea geometriei suprafetelor de nivel (inclusiv a geoidului) deoarece curbura acestora depinde de densitatea r. Din acest motiv este imposibila o formulare analitic-matematica a acestei suprafete complexe, dependenta in permanenta de distributia si densitatea maselor in interiorul Pamantului.
Geoidul este definit uzual ca suprafata medie a marilor linistite prelungita pe sub continente.
H. Bruns a formulat scopul principal al geodeziei fizice ca fiind determinarea suprafetelor de nivel ale campului gravitatii, ceea ce echivaleaza cu determinarea functiei potential W(x, y, z). In adevar, cunoscand expresia potentialului unui corp, se pot face estimari privind forma suprafetei sale.
Deoarece suprafetele de nivel sunt suprafete echipotentiale, diferenta de potential dintre doua suprafete de nivel este o marime constanta. Rezulta ca cresterea de potential (deci de lucru mecanic) nu depinde de drumul parcurs, pentru trecerea unui punct de pe o suprafata de nivel pe alta (traseul 1 sau traseul 2 in Fig. 2.14).
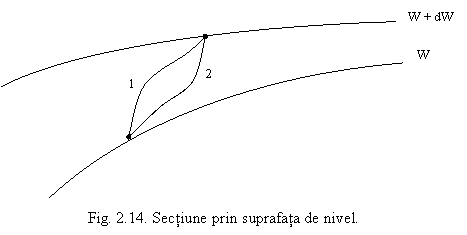
Prin urmare, suma cresterilor de potential pe un contur inchis, indiferent de sensul de parcurgere, este zero:
![]() (2.86)
(2.86)
O alta directie importanta pentru geodezie este directia h, paralela cu directia gravitatii, adica perpendiculara la suprafata de nivel:
![]() (2.87)
(2.87)
Pentru departarea dintre suprafetele de nivel
se alege sensul crescator spre exteriorul suprafetei Pamantului (sensul invers fortei ![]() ) si ca urmare din relatia (2.87) se va lua
semnul minus. Cu aceasta, se obtine din relatia de baza (2.55)
) si ca urmare din relatia (2.87) se va lua
semnul minus. Cu aceasta, se obtine din relatia de baza (2.55)
![]() (2.88)
(2.88)
sau
![]() (2.89)
(2.89)
unde dh reprezinta distanta dintre suprafetele de nivel caracterizate prin potentialele W si respectiv W + dW.
Relatiile (2.88) si (2.89) reprezinta un exemplu de legatura dintre aspectul geometric h si cel dinamic W in cadrul problematicii abordate in geodezia fizica.
Deoarece gec < gpol, rezulta ca distanta dintre doua suprafete de nivel se micsoreaza de la ecuator spre pol, deci suprafetele de nivel nu sunt paralele intre ele.
Din relatia (2.88) se mai poate deduce o proprietate remarcabila a suprafetelor de nivel. Deoarece intre doua suprafete de nivel g nu poate lua niciodata valoarea infinit, rezulta ca distanta dh, dintre aceste suprafete nu poate fi niciodata zero. Aceasta inseamna ca suprafetele de nivel nu se ating si nu se intretaie niciodata.
Se poate demonstra ca suprafetele de nivel
sunt suprafete continue, inchise, fara muchii sau varfuri. Rezulta ca liniile
care intersecteaza suprafetele de nivel sub unghiuri drepte, vor avea o anumita
curbura. Ele se numesc linii de forta.
Tangenta la linia de forta intr-un punct P da directia gravitatii
![]() , care poate fi materializata
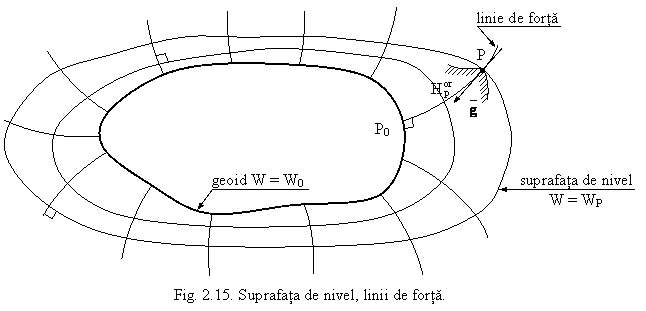
prin directia firului cu plumb. O imagine aproximativa, intuitiva, a
suprafetelor de nivel si liniilor de forta este reprezentata in Fig. 2.15.
, care poate fi materializata
prin directia firului cu plumb. O imagine aproximativa, intuitiva, a
suprafetelor de nivel si liniilor de forta este reprezentata in Fig. 2.15.
Segmentul de linie de forta cuprins intre
pozitia punctului pe suprafata fizica a Pamantului P si proiectia sa pe geoid P0
se numeste altitudinea ortometrica
![]()
2. Consecintele neparalelismului suprafetelor de nivel. Pentru a urmari unele dintre consecintele
neparalelismului suprafetelor de nivel pentru lucrarile geodezice, ne vom
referi la sistemul de altitudini
ortometrice, in care geoidul este
suprafata de referinta iar altitudinea ortometrica este segmentul de linie de
forta cuprins intre pozitia punctului, pe suprafata terestra, si respectiv pe
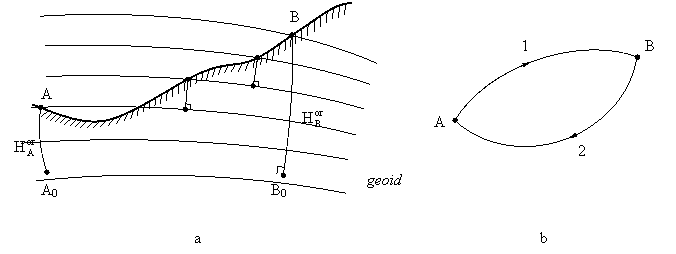
geoid. Din figura 2.16-a se observa ca suma diferentelor de nivel
elementare, masurate pe traseul cuprins intre punctele A si B, notata ![]() nu este
egala cu diferenta altitudinilor ortometrice ale punctelor A si B,
notate
nu este
egala cu diferenta altitudinilor ortometrice ale punctelor A si B,
notate ![]() si
si ![]()
Cu aceasta remarca se pune in evidenta faptul
ca rezultatul obtinut direct prin lucrarile de nivelment geometric ![]() este dependent de traseul parcurs.
este dependent de traseul parcurs.
Generalizand (Fig. 2.16-b), rezulta ca sumele diferentelor de nivel elementare, masurate pe traseele 1 si 2, nu vor fi egale intre ele, nici chiar in cazul ideal al observatiilor geodezice perfecte, fara erori de masurare. In consecinta, in poligonul format, va rezulta o neinchidere, care se mai numeste si eroare de principiu a nivelmentului geometric geodezic.
Fig. 2.16. Consecintele neparalelismului suprafetelor de nivel
asupra determinarilor nivelitice pe linii si poligoane de mari dimensiuni.
Pentru a obtine un control corect in lucrarile de nivelment geometric de ordin superior este necesar ca in paralel sa se efectueze si determinari gravimetrice, pentru calculul diferentelor de potential:
![]() (2.90)
(2.90)
sau, intr-o aproximatie impusa de posibilitatile practice:
![]() (2.91)
(2.91)
Pe un contur inchis:
![]() (2.92)
(2.92)
Nivelmentul geometric superior fara determinari gravimetrice este lipsit de rigoarea necesara unor astfel de lucrari, controlul efectuat prin calcularea neinchiderilor in poligoane fiind afectat de erorile de principiu mentionat anterior:
![]() (2.93)
(2.93)
Pentru liniile si poligoanele de nivelment de mari dimensiuni, specifice retelelor de nivelment geodezic de stat, simpla insumare a diferentelor de nivel masurate nu este suficienta pentru transmiterea altitudinilor. Este necesar sa se lucreze cu marimi derivate, corectate, in functie de sistemul de altitudine adoptat.
![]() pentru geodezie ; (2.94)
pentru geodezie ; (2.94)
![]() pentru topografie (cand se presupune g = constant); (2.95)
pentru topografie (cand se presupune g = constant); (2.95)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3959
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved