| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
DIFERENCE A DIFERENČNÍ ROVNICE (DR)
§1 Funkce a posloupnosti
Termínem funkce budeme nadále rozumět reálnou funkci
jedné reálné proměnné definovanou na intervalu J. Termínem posloupnost budeme rozumět
reálnou posloupnost definovanou na množině ![]() . Posloupnost budeme zapisovat
. Posloupnost budeme zapisovat ![]() např.
posloupnost
např.
posloupnost ![]()
V některých konkrétních situacích bude vhodnější
posloupnost definovat na množině přirozených čísel N resp. na množině ![]() , kde r je pevně zvolené přirozené číslo,
nebo omezit se na konečné množiny
, kde r je pevně zvolené přirozené číslo,
nebo omezit se na konečné množiny ![]() kde r,
t jsou přirozená čísla, r < t. Pokud nebude definiční obor
posloupnosti blíže specifikován, budeme předpokládat, že je roven N0.
kde r,
t jsou přirozená čísla, r < t. Pokud nebude definiční obor
posloupnosti blíže specifikován, budeme předpokládat, že je roven N0.
§2 Diference
V řadě problémů ekonomické praxe se setkáváme s funkcemi danými nikoli obecným funkčním předpisem, ale tabulkou funkčních hodnot. Na takto zadanou funkci lze pohlížet jako na (konečnou) posloupnost; zdá se proto užitečné vybudovat pro posloupnosti teorii odpovídající diferenciálnímu počtu funkcí definovaných na intervalu J, s pojmy odpovídajícími derivaci, integrálu a diferenciální rovnici. Tuto teorii nazvěme diferenční počet. Dá se ukázat, že analogickým pojmům z diferenciálního a diferenčního počtu odpovídají i analogická tvrzení.
Diferenční rovnice vlastně představují rekurentní vzorec pro posloupnost a jejich řešení je tzv. funkční vzorec. Tak například pro aritmetickou posloupnost je rekurentní vzorec
![]() diferenční rovnice
diferenční rovnice
a vzorec funkční
![]() řešení
řešení
Výhoda funkčního vzorce spočívá v tom, že počet operací, které v němž jsou obsaženy a potřebné k výpočtu určitého an nezávisí na velikosti n.
Nyní zavedeme analogii pojmu derivace.
|
Definice : Uvažujme posloupnost
se nazývá diference posloupnosti |
Poznámka: Např. diferencí posloupnosti ![]() je
posloupnost
je
posloupnost ![]()
Příklad : Stanovme diference posloupností
![]() CIR,
CIR,
![]()
![]()
![]()
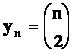
Řešení : Dosazením do
definičního vzorce ![]() dostáváme
dostáváme
![]()
![]()
![]()
![]()
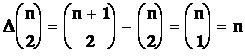
Přímo z definice diference vyplývá
|
Věta : (o diferenci aritmetických operacích). Nechť |
Důkaz : Dokažme např. )
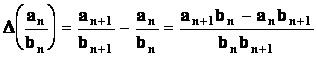
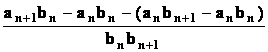
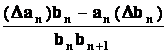
Příklad : Stanovme diferenci
posloupnosti bn = ![]()
Řešení : Platí
Dbn = D![]()
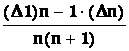
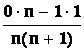
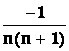
Vyšší diference
Diference ![]() členů posloupnosti
členů posloupnosti ![]() tvoří posloupnost
tvoří posloupnost ![]() ; z členů této posloupnosti lze opět vypočítat diference, tzv. druhé diference posloupnosti
(an). Označíme je
; z členů této posloupnosti lze opět vypočítat diference, tzv. druhé diference posloupnosti
(an). Označíme je ![]() ; definujeme tedy
; definujeme tedy
![]()
![]()
Zcela analogicky definujeme třetí diferenci
![]()
![]()
Obecně definujeme k‑tou diferenci:
![]()
![]()
Místo „k‑tá diference“ též říkáme „diference k‑tého řádu“.
Příklad :
Stanovme ![]()
Řešení : Pomocí definice druhé diference, věty o diferenci násobku posloupnosti a věty o diferenci exponenciály dostáváme:
![]()
![]()
![]()
![]()
![]()
=![]()
![]()
![]()
Příklad :
Vyjádříme druhou diferenci pomocí členů posloupnosti ![]()
![]()
![]()
![]()
![]()
Obecně platí následující věta (lze ji dokázat matematickou indukcí)
|
Věta : o k‑té diferenci Uvažujme posloupnost
|
§3 Diferenční rovnice
Tak jako v diferenciálním počtu studujeme tzv. diferenciální rovnice, tj. rovnice obsahující neznámou funkci a její derivace, tak v diferenčním počtu diferenční rovnice představují rovnice o neznámé posloupnosti a jejích diferencích:
|
Definice: Nechť g je funkce dvou proměnných definovaná na Nr R. Rovnice
o neznámé posloupnosti |
Poznámka :
Řešit danou diferenční rovnici znamená nalézt posloupnost ![]() vyhovující
dané rovnici pro všechna nINr , tj. pro všechna
n = r, r+1, ¼ . Předpoklad, že daná posloupnost je řešením dané
rovnice, nejsnáze ověříme tak, že ji do dané rovnice dosadíme. Např. řešením
diferenční rovnice
vyhovující
dané rovnici pro všechna nINr , tj. pro všechna
n = r, r+1, ¼ . Předpoklad, že daná posloupnost je řešením dané
rovnice, nejsnáze ověříme tak, že ji do dané rovnice dosadíme. Např. řešením
diferenční rovnice
![]()
je yn = ![]()
![]() +C,
+C,
neboť
![]()
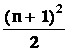
![]() +C
+C ![]()
![]() +C) = n
+C) = n
Poznámka : Řešení závislé na obecné konstantě se nazývá obecné řešení. Konkrétní volbou konstanty C dostáváme tzv. partikulární řešení; je tedy obecné řešení vzorcem popisujícím množinu všech partikulárních řešení. Partikulární řešení lze sestrojit z obecného také jinak než dosazením za konstantu, a to pomocí tzv. počátečních podmínek. Jsou to souřadnice bodu, jímž má graf partikulárního řešení procházet. Někdy se vyskytuje řešení, jež nezávisí na obecné konstantě ani ho nelze sestrojit z obecného. Takové řešení se nazývá singulární.
Příklad :
Nechť obecným řešením diferenční rovnice je ![]() . Stanovme partikulární řešení procházející bodem
. Stanovme partikulární řešení procházející bodem ![]()
Řešení : Graf
partikulárního řešení (posloupnosti) má procházet bodem ![]() , tj. pátý člen posloupnosti má být roven dvěma, tj.
, tj. pátý člen posloupnosti má být roven dvěma, tj.
y5 = ![]() Þ C = 15
Þ C = 15
Partikulární řešení má tedy tvar
y5 = ![]()
Diferenční rovnice vyšších řádů
Definice: Uvažujme funkci g o (k + 1) proměnných definovanou na množině Nr Rk. Rovnice
![]()
o neznámé
posloupnosti ![]() , nINr se nazývá diferenční
rovnice k‑tého řádu v Nr .
, nINr se nazývá diferenční
rovnice k‑tého řádu v Nr .
Poznámka : Diference v uvedené rovnici lze nahradit hodnotami členů posloupnosti (yn) podle vzorce
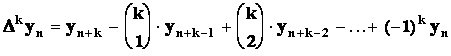
Po úpravě a osamostatnění ![]() dostáváme
diferenční rovnici k‑tého řádu ve tvaru
dostáváme
diferenční rovnici k‑tého řádu ve tvaru
![]()
kde h je funkce vzniklá z funkce g osamostatněním
![]() na levé straně rovnice.
na levé straně rovnice.
§4 Lineární diferenční rovnice
|
Definice : Rovnice
o neznámé posloupnosti |
Dále označujeme
F(n) ¼ obecné řešení lineární rovnice,
y(n) ¼ partikulární řešení lineární rovnice,
![]() (n) ¼ obecné řešení zkrácené rovnice,
(n) ¼ obecné řešení zkrácené rovnice,
Příklad : Rovnice yn+1 + (ln n)yn = n2 je lineární rovnice 1. řádu, zatímco rovnice yn+1 + n(yn)2 = 1 lineární není - podstatné je, aby se členy neznámé posloupnosti yn v dané rovnici vyskytovaly pouze jako lineární kombinace; koeficienty této lineární kombinace, tj. dané posloupnosti (pi(n)) a posloupnost (qn) nemusí být lineární.
Příklad : Rovnice yn+1 ‑ n2yn ‑ 3n = 0 není zkrácená, kdežto rovnice yn+1 = 2nyn zkrácená je - nezáleží totiž na zápisu rovnice, ale na tom, zda rovnice kromě výrazů zahrnující členy neznámé posloupnosti (yn) obsahuje ještě další nenulový výraz. V prvém případě je obvyklejší psát yn+1 ‑ n2yn = 3n , v druhé případě yn+1 ‑ 2nyn = 0.
Pro lineární rovnice platí dvě základní věty:
|
Věta o množině řešení lineární rovnice Všechna řešení lineární rovnice vytvoříme tak, že k jednomu pevně zvolenému řešení této rovnice přičteme všechna řešení příslušné rovnice zkrácené, neboli
|
|
Věta o množině řešení zkrácené rovnice Všechna řešení zkrácené rovnice k‑tého řádu tvoří vektorový prostor dimenze k, neboli
kde |
zkrácená diferenční rovnice s konstantními koef.
Uvažujme zkrácenou rovnici
![]()
pro nIN0 , kde p1, p2, ¼, pk jsou reálné konstanty. Předpokládejme dále, že pk ¹
Řešením zkrácené rovnice je posloupnost yn = ln ; po dosazení uvedené posloupnosti do rovnice totiž dostáváme
![]()
Pokud tuto rovnici dělíme výrazem ![]() , l ¹ 0, dostáváme tzv. charakteristickou rovnici příslušnou k zkrácené rovnici:
, l ¹ 0, dostáváme tzv. charakteristickou rovnici příslušnou k zkrácené rovnici:
![]()
Stanovení všech řešení závisí na typu kořenů charakteristické rovnice
Charakteristická rovnice má k různých reálných kořenů l l ¼ lk
Každé řešení této rovnice lze napsat ve tvaru
![]()
kde c1, c2 , ¼,ck jsou reálné konstanty.
Příklad : Řešme diferenční rovnici ![]()
Řešení : Charakteristická rovnice má tvar
![]()
Kořeny jsou l l Þ ![]()
2.) Případ k‑násobného reálného kořenu l . Každé řešení této rovnice lze
napsat ve tvaru
![]()
kde c1, c2 , ¼,ck jsou reálné konstanty.
Příklad : Řešme rovnici ![]()
Řešení : Charakteristická rovnice má tvar
![]()
Kořeny jsou l = 1 (jednoduchý), l = 3 (dvojnásobný)
Þ ![]()
Dvojice komplexně sdružených kořenů l = a + ib, l = a ib.
Převedeme kořen l na goniometrický tvar:
![]()
Komplexní řešení ![]() lze při použití Moivreovy věty
psát ve tvaru
lze při použití Moivreovy věty
psát ve tvaru
![]()
Potom platí
![]()
kde c1, c2 jsou reálné konstanty.
Příklad : Řešme diferenční rovnici ![]()
Řešení : Charakteristická rovnice má tvar
![]()
a její kořeny jsou ![]() a
a ![]()
Převeďme na goniometrický tvar
![]()
Þ ![]()
Platí tedy
![]()
lineární diferenční rovnice s konstantními koef.
Uvažujme rovnici
![]()
pro nIN0 , kde p1, p2, ¼, pk jsou reálné konstanty. Předpokládejme dále, že pk ¹
Platí ![]()
Věta o partikulárním řešení lineární rovnice s konstantními koeficienty
Nechť pravá
strana qn=![]() , kde
, kde ![]() je polynom m‑tého stupně. Potom je jedno partikulární řešení tvaru
je polynom m‑tého stupně. Potom je jedno partikulární řešení tvaru
![]()
kde ![]() je vhodný polynom m‑tého stupně a k je násobnost čísla r jako kořen charakteristické rovnice.
je vhodný polynom m‑tého stupně a k je násobnost čísla r jako kořen charakteristické rovnice.
Příklad :
Řešme diferenční rovnici ![]()
Řešení
Charakteristická rovnice příslušná zkrácené rovnici má tvar
![]()
Má dvojnásobný kořen l Þ ![]()
Platí qn=![]() , kde m = 0 , r Þ k = 0. Položíme tedy
, kde m = 0 , r Þ k = 0. Položíme tedy
![]()
![]() = A
= A
Zbývá vypočítat hodnotu konstanty A dosazením odhadu y(n) do rovnice ![]()
Þ A 4A + 4A = 1 Þ A = 1 Þ y(n) = 1
![]()
![]()
Příklad :
Stanovme partikulární řešení diferenční
rovnice ![]() vyhovující počáteční podmínce
vyhovující počáteční podmínce ![]()
Řešení
Charakteristická rovnice příslušná zkrácené rovnici má tvar
![]()
Þ l Þ ![]()
Platí qn=![]() , kde m = 1, r Þ k = 1. Položíme
tedy
, kde m = 1, r Þ k = 1. Položíme
tedy
![]()
![]()
![]()
Zbývá vypočítat hodnotu konstant A a B dosazením odhadu y(n) do rovnice
![]()
Þ ![]()
![]()
![]()
![]()
Þ ![]()
![]()
Þ 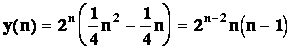
3. Obecné
řešení ![]()
![]()
partikulární řešení
vyhovující počáteční podmínce ![]() dostaneme z
dostaneme z
rovnice
![]() Þ
Þ ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1104
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved