| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Diferenciální počet funkce jedné reálné proměnné
Zobrazíme‑li množinu přirozených čísel do množiny reálných čísel, dostaneme posloupnost reálných čísel.
Posloupnost zapisujeme a1, a2,
¼, an, ¼,
nebo ![]() ,
nebo
,
nebo ![]() .
.
an nazýváme obecným členem posloupnosti.
Příklady posloupností:
a)
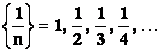
![]()
b)
![]()
![]()
c)
![]()
![]()
Někdy bývají posloupnosti zadány rekurentním vzorcem, tj. obecný člen je dán pomocí několika členů předcházejících. Přitom je dána hodnota určujících členů.
Např. an = an-1 + an-2, a1 = 1, a2 = 1 (Fibonacciova posloupnost), tedy 1, 1, 2, 3, 5, 8, 13, 21, ¼
Vlastnosti posloupností
Posloupnost ![]() se nazývá
se nazývá
rostoucí, když pro
všechna n platí ![]()
klesající ![]()
neklesající ![]()
nerostoucí ![]()
Společný název pro tyto posloupnosti je ‑ posloupnost monotónní, z nichž typy 1. a 2. se nazývají ryze monotónní.
Příklad:
Dokažte, že posloupnost 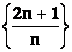 je klesající.
je klesající.
Řešení: Pro klesající posloupnost platí ![]() ,
tj.
,
tj. ![]() n.
n.
![]()
![]()
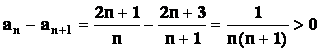 .
.
Další vlastnosti posloupností
Je‑li množina všech členů posloupnosti
![]() taková,
že
taková,
že
k I R, n I N : an £ k
říkáme, že posloupnost ![]() je shora
omezená (ohraničená). Podobně posloupnost
je shora
omezená (ohraničená). Podobně posloupnost ![]() je zdola
omezená (ohraničená), když
je zdola
omezená (ohraničená), když
l I R, n I N : an ³ l
Posloupnost , která je shora i zdola omezená, se
nazývá omezená
(ohraničená). Pro všechny členy platí ![]() .
.
Definice: Číslo L je limita posloupnosti ![]() ,
jestliže ke každému e > 0
existuje číslo n0 tak, že pro všechna
n > n0 platí nerovnost
,
jestliže ke každému e > 0
existuje číslo n0 tak, že pro všechna
n > n0 platí nerovnost ![]() .
.
Zapisujeme
![]()
Zápis předešlé definice lze vyjádřit
![]() IN tak, že n>
IN tak, že n>![]() platí
platí ![]() .
.
Podle definice je jen konečný počet členů posloupnosti, nejvýše n0
takových, že ![]() .
Říkáme, že uvedená podmínka
.
Říkáme, že uvedená podmínka ![]() musí
být splněna pro skoro všechny
členy posloupnosti.
musí
být splněna pro skoro všechny
členy posloupnosti.
Posloupnost a1, a2,
¼, an, ¼,
můžeme znázornit body o souřadnicích [1, a1], [2, a2],
¼, [n, an], ¼ . Má‑li
být číslo L limitou této posloupnosti, musí skoro všechny členy
splňovat nerovnost ![]() ,
tj. jejich obrazy musí ležet v pásu
,
tj. jejich obrazy musí ležet v pásu ![]() a jen konečný počet, nejvýše n0 , může být zobrazeno mimo
tento pás.
a jen konečný počet, nejvýše n0 , může být zobrazeno mimo
tento pás.
Posloupnost, která má limitu, nazýváme konvergentní posloupnost. Posloupnost, která není konvergentní, je divergentní.
Příklad:
Dokažte podle definice, že ![]() .
.
Řešení: Je třeba dokázat, že pro libovolné e > 0, platí pro skoro všechna n nerovnost
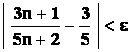 .
Lze ji upravit na
.
Lze ji upravit na 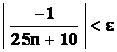 .
.
Stačí dokázat, že tato nerovnost není splněna jen pro konečný počet čísel. Z poslední nerovnosti vychází, že není splněna, pokud platí
![]() neboli
neboli ![]() ,
tedy pro
,
tedy pro 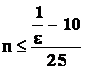 .
.
Takových n je pro každé e > 0 zřejmě jen konečný počet.
Poznámka:
Zdůrazněme znovu, že v definici limity posloupnosti velikost voleného čísla
e > 0 ovlivňuje počet
členů, které nesplňují nerovnost ![]() ,
stále je jich však pouze konečný počet.
,
stále je jich však pouze konečný počet.
Počítat limity posloupností přímo z definice by bylo většinou obtížné. K výpočtům užíváme vlastností posloupností a věty o limitách posloupností. Věty jsou uvedeny bez důkazů.
Každá konvergentní posloupnost má právě jednu limitu.
Konvergentní posloupnost je vždy omezená. Důsledek : Každá neomezená posloupnost je divergentní.
Poznámka: Obrácená věta neplatí. Posloupnost, která je omezená, nemusí mít
limitu (nemusí být konvergentní). Např. posloupnost ![]() je omezená, nemá však limitu.
je omezená, nemá však limitu.
Omezená posloupnost, která je monotónní, má limitu.
Často užívaná bude posloupnost
![]() .
Pro ni platí
.
Pro ni platí ![]() .
.
Nechť ![]() a
a ![]() jsou konvergentní, přičemž
jsou konvergentní, přičemž
 a
a
Pak platí :
![]()
![]() , odtud
, odtud ![]() ,
c I R
,
c I R
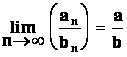 pro b ¹
pro b ¹
Použití ukážeme na příkladech.
Příklad1:
Určete 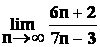 .
.
Řešení: Protože posloupnosti ![]() ,
,
![]() nejsou konvergentní, jak vyžaduje předpoklad vět o limitách, nelze přímo užít
věty o podílu limit (
nejsou konvergentní, jak vyžaduje předpoklad vět o limitách, nelze přímo užít
věty o podílu limit (![]() ).
Proto čitatel i jmenovatel zlomku vynásobíme
).
Proto čitatel i jmenovatel zlomku vynásobíme ![]()
 (neboť
(neboť ![]() )
)
Příklad2:
Určete ![]() .
.
Řešení: Výraz v limitě upravíme

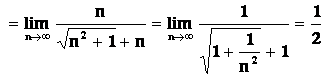
Poznámka:
Tento obrat je často používaný. Používáme vzorce ![]() ,
pokud ve výrazu a ‑ b vystupují druhé odmocniny.
Analogicky lze upravit
,
pokud ve výrazu a ‑ b vystupují druhé odmocniny.
Analogicky lze upravit 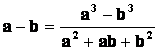 ,
vystupují‑li ve výrazu a ‑ b třetí odmocniny.
,
vystupují‑li ve výrazu a ‑ b třetí odmocniny.
Příklad3:
Vypočtěte 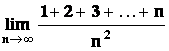
Řešení: Výraz v čitateli můžeme sečíst jako n členů aritmetické
posloupnosti ![]() ,
tedy
,
tedy
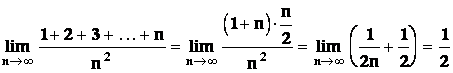
Číslo e
Dá se dokázat, že posloupnost 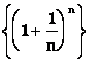 má limitu, kterou označíme e (Eulerovo číslo), tj.
má limitu, kterou označíme e (Eulerovo číslo), tj.
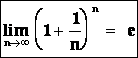
Poznámka: Číslo e je důležitá konstanta, kterou vhodným postupem lze vypočítat na libovolný počet desetinných míst: e ¼
Této odvozené limity lze použít při výpočtech :
Příklad4:
Vypočtěte 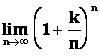 ,
k>
,
k>
Řešení: Výraz ![]() nahradíme výrazem
nahradíme výrazem ![]() ,
tzn. n = k m Þ když n ¥ , také m ¥
,
tzn. n = k m Þ když n ¥ , také m ¥
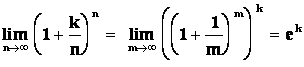
Příklad5:
Vypočtěte 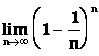 .
.
Řešení
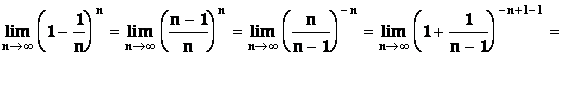
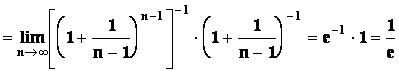
Příklad6:
Vypočtěte 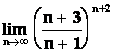 .
.
Řešení
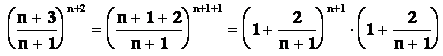
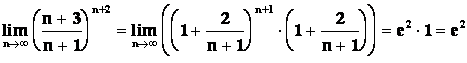
Definice: Posloupnost ![]() má nevlastní
limitu +¥ ,
(resp. ¥), existuje‑li ke každému
K číslo n0 tak, že pro všechna
n > n0 je an > K
(resp. an < K ).
má nevlastní
limitu +¥ ,
(resp. ¥), existuje‑li ke každému
K číslo n0 tak, že pro všechna
n > n0 je an > K
(resp. an < K ).
Zápis
![]() resp.
resp. ![]()
Zápis předešlé definice lze vyjádřit
![]() Û K n0
tak, že
Û K n0
tak, že ![]() .
.
Poznámka: Má‑li posloupnost nevlastní limitu +¥ , resp. ‑¥, říkáme, že její členy rostou nade všechny meze, resp. klesají pode všechny meze.
Příklad:
Dokažme, že ![]() .
.
Řešení: Podle definice musí existovat číslo n0 tak,
aby pro všechna n > n0 platilo an > K .
Takové číslo lze vždy určit ![]() .
Budeme‑li např. K = 1000 bude n0 = 10
pro K = 106 bude n0 = 100
atd.
.
Budeme‑li např. K = 1000 bude n0 = 10
pro K = 106 bude n0 = 100
atd.
Nechť D a H jsou dvě neprázdné množiny. Je‑li každému prvku x I D přiřazen právě jeden prvek y I H , je definováno zobrazení množiny D do množiny H . Jsou‑li přitom vyčerpány všechny prvky množiny H , jde o zobrazení množiny D na množinu H .
Nechť je dáno zobrazení f číselné množiny D Ì R na číselnou množinu H Ì R . Zobrazení f nazveme funkcí jedné proměnné, přičemž D nazýváme definičním oborem funkce f a H oborem hodnot funkce f.
Proměnnou x nazýváme nezávisle proměnnou, případně argumentem funkce f , y pak závislou proměnnou.
Vyjádření funkcí bývá nejčastěji zadáno
a) výrokovou formou
b) tabulkou
c) grafem
Je‑li funkce zadána výrokovou formou, pak výroková forma může mít tvar rovnice nebo slovního vyjádření. Většinou se používá zápisu
y = f(x), x I D
Je‑li funkce zadána tabulkou, jsou zadány zvolené hodnoty nezávislé proměnné veličiny a na dalším řádku jsou odpovídající hodnoty závisle proměnné veličiny.
Grafem funkce nazveme množinu
všech bodů v E2 o souřadnicích ![]() ,
kde xID, f(x)IH.
,
kde xID, f(x)IH.
Definiční obor funkce
Je‑li určen jen funkční předpis bez definičního oboru, je definičním oborem maximální množina, pro kterou má předpis smysl. Např.
![]()
Tento výraz má smysl pro x + 2 ³ 0,
tedy x ³ -2, tj. D(f) = ![]() .
.
Při určování definičního oboru se řídíme vlastnostmi, které podmiňují reálnou hodnotu funkce.
Ve zlomku musí být jmenovatel různý od nuly.
Sudá odmocnina je definována jen pro nezáporná čísla.
Logaritmus je definován pouze pro kladná čísla.
Funkce arcsin(x) a arccos(x) jsou definovány jen pro x I![]()
Příklad1 : Rozhodněte, zda relace ![]() je funkcí.
je funkcí.
Řešení: Je třeba zjistit, zda ke každému x0 I R existuje nejvýše jedno y0 I R takové, že platí ![]() .
Pro x0 < 0 neexistuje y0 I R takové, aby platilo
.
Pro x0 < 0 neexistuje y0 I R takové, aby platilo ![]() ;
pro x0 = 0 existuje právě jedno y0 I R , že výrok
;
pro x0 = 0 existuje právě jedno y0 I R , že výrok ![]() je pravdivý. Pro x0 > 0 existují dvě
vzájemně různá reálná čísla
je pravdivý. Pro x0 > 0 existují dvě
vzájemně různá reálná čísla ![]() a
a ![]() ,
pro která je výrok
,
pro která je výrok ![]() a
a ![]() pravdivý. Relace tedy není funkcí.
pravdivý. Relace tedy není funkcí.
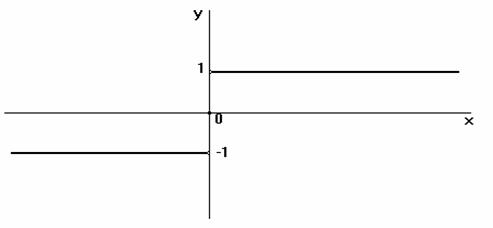
Příklad2 : Nakreslete graf funkce ![]() ,
která je definována takto: pro x < 0 je její hodnota
y = ‑1, pro x = 0 je
y = 0 , pro x > 0 je
y = 1.
,
která je definována takto: pro x < 0 je její hodnota
y = ‑1, pro x = 0 je
y = 0 , pro x > 0 je
y = 1.
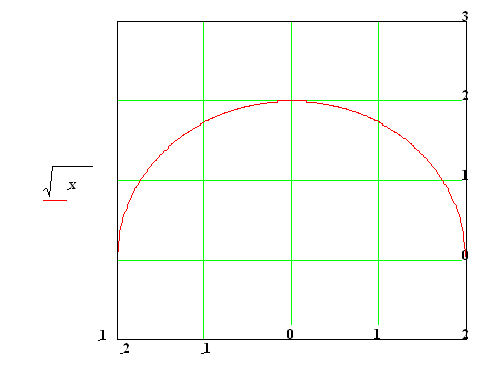
Příklad3 : Najděte definiční obor a zobrazte
funkci ![]() .
.
Řešení: Definiční obor je dán podmínkou ![]()
![]() . Graf je horní polovina kružnice o poloměru 2, se středem v bodě
. Graf je horní polovina kružnice o poloměru 2, se středem v bodě ![]() .
.
Některé vlastnosti funkcí:
Pro funkce monotonní v D platí x1 I D, x2 I D
f je rostoucí v D Û x1 < x2 Þ f(x1) < f(x2)
f je klesající v D Û x1 < x2 Þ f(x1) > f(x2)
f je neklesající v D Û x1 < x2 Þ f(x1) £ f(x2)
f je nerostoucí v D Û x1 < x2 Þ f(x1) ³ f(x2)
f je shora resp. zdola omezená v D, existuje‑li číslo K1 resp. K2 takové, že pro všechna x I D platí f(x) £ K1, resp. f(x) ³ K2
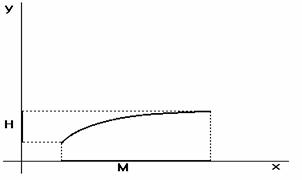
f je prostá v D ![]()
Obrázek funkce prosté :
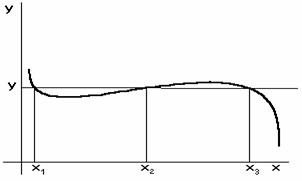
Obrázek funkce, která není prostá :
Funkce f je periodická, existuje‑li číslo
p takové, že pro x I D platí ![]() ,
neboli
,
neboli ![]() .
.
Nejmenší kladné číslo této vlastnosti nazýváme periodou funkce f
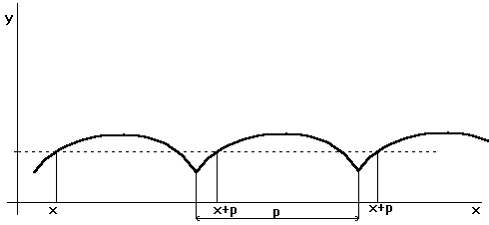
Funkce f se nazývá
sudá, jestliže f(x) = f(‑x) pro x I D ( tj. graf je souměrný podle osy y),
lichá, jestliže f(-x) = ‑f(x) pro x I D ( tj. graf je souměrný podle počátku).
Nechť f je zobrazení množiny A do množiny B, g je zobrazení množiny B do množiny C. Potom zobrazení h definované
![]()
zobrazuje množinu A do množiny C a nazývá se zobrazení složené. Jsou‑li A, B, C číselné množiny, pak h je funkce složená z funkcí f a g. Platí:
D(h) =![]()
Např. z = sin x3
je složená y = x3 , z = sin y
Poznámka: Ve
složené funkci ![]() nazýváme
f funkcí vnitřní
a g funkcí vnější.
Funkce může být i několikrát složená. Např.
nazýváme
f funkcí vnitřní
a g funkcí vnější.
Funkce může být i několikrát složená. Např. ![]() Þ
Þ ![]() .
.
Nechť f : y = f(x)
x I A je funkce prostá. Oborem
funkčních hodnot je H = B. K prostému zobrazení existuje
inverzní zobrazení, které každému y I B přiřazuje jediné x I A , pro které f(x) = y. Toto zobrazení
značíme ![]() .
Grafy funkcí y = f(x) a x = f (y) jsou totožné, neboť u funkcí
f a f je vyměněna pouze závislost
proměnných. Definiční obor D(f) = A funkce f
bude oborem funkčních hodnot H(f ‑1) = A
funkce f ‑1 a obor funkčních hodnot
H(f) = B funkce f bude definičním oborem
D(f ‑1) = B funkce f . Chceme‑li nezávisle proměnnou
vynášet na vodorovnou osu x , provedeme přeznačení : u funkce x = f ‑1(y)
bude nezávisle proměnná opět značena x a závisle proměnná
y , tedy y = f ‑1(x).
.
Grafy funkcí y = f(x) a x = f (y) jsou totožné, neboť u funkcí
f a f je vyměněna pouze závislost
proměnných. Definiční obor D(f) = A funkce f
bude oborem funkčních hodnot H(f ‑1) = A
funkce f ‑1 a obor funkčních hodnot
H(f) = B funkce f bude definičním oborem
D(f ‑1) = B funkce f . Chceme‑li nezávisle proměnnou
vynášet na vodorovnou osu x , provedeme přeznačení : u funkce x = f ‑1(y)
bude nezávisle proměnná opět značena x a závisle proměnná
y , tedy y = f ‑1(x).
Þ Grafy funkcí f a f ‑1 budou souměrné podle přímky y = x.
Není‑li v celém oboru funkce f prostá, musíme se omezit jen na tu jeho část, v níž je f prostá funkce.
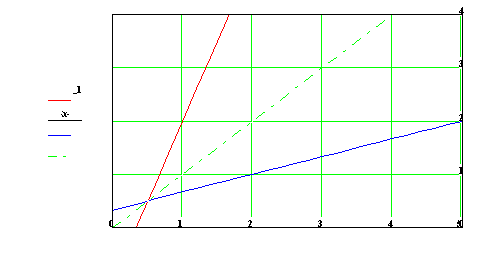
Příklad1:
Najděte inverzní funkci a její graf k funkci ![]() .
.
Řešení: D = H = ![]() ,
v celém intervalu je funkce prostá.
,
v celém intervalu je funkce prostá.
Z rovnice vypočteme x : ![]() .
.
Přeznačíme proměnné f ‑1 :
![]()
D(f ‑1) = ![]() ,
H(f ‑1) =
,
H(f ‑1) =![]() .
.
Grafy budou souměrné podle přímky y = x
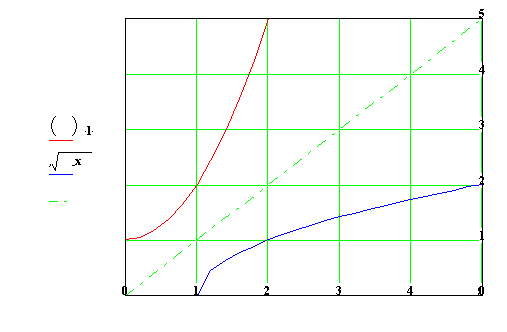
Příklad2:
Najděte inverzní funkci a její graf k funkci y = ![]() .
.
Řešení: D(f) = ![]() ,
H(f) =
,
H(f) = ![]() .
Je třeba se omezit na interval, v němž je funkce prostá.
.
Je třeba se omezit na interval, v němž je funkce prostá.
Např. D(f) = ![]() H(f) =
H(f) = ![]()
Z rovnice vypočteme x : ![]() .
.
Přeznačíme proměnné f ‑1 : ![]()
D(f ‑1) = ![]() H(f ‑1) =
H(f ‑1) = ![]()
Graf
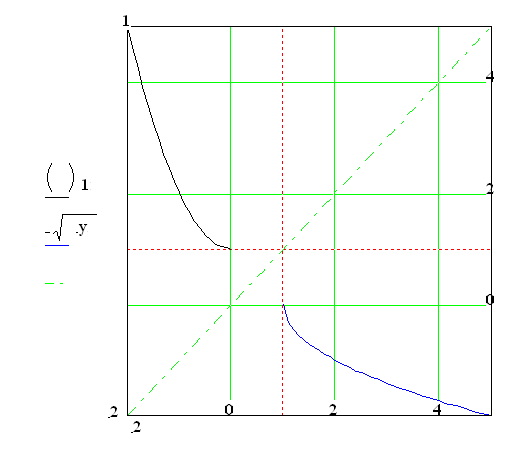
Pro D(f) = ![]() , H(f) =
, H(f) =![]()
Z rovnice vypočteme x : ![]() .
.
Přeznačíme proměnné f ‑1 : ![]()
D(f ‑1) = ![]() , H(f ‑1) =
, H(f ‑1) = ![]()
Graf bude
Jejich definiční obor budeme označovat D, obor funkčních hodnot H.
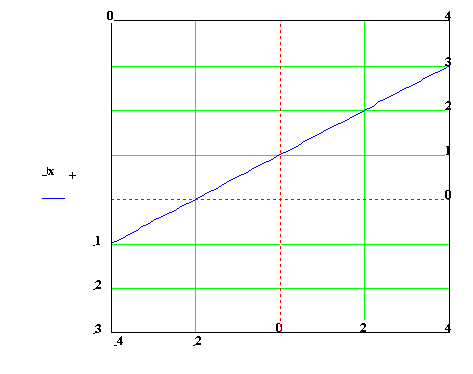
Lineární funkce je každá funkce daná předpisem
![]()
kde k, q I R. Platí D = H = R (pro k ¹
Grafem je přímka,
která svírá s kladnou osou úhel a takový, že tg a = k a prochází bodem Q=![]() na ose y. K určení grafu
přímky potřebujeme znát dva body nebo jeden bod a úhel a
na ose y. K určení grafu
přímky potřebujeme znát dva body nebo jeden bod a úhel a
Lineární funkce je prostá pro všechna k ¹
a) je rostoucí pro k >
b) je klesající pro k <
c) je konstatní pro k = 0 .
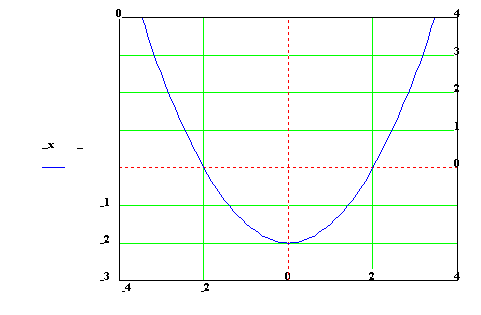
Kvadratická funkce je každá funkce daná předpisem
![]()
kde a ¹ 0 , a, b, c I R , D = R.
Lineární lomená funkce je funkce daná předpisem
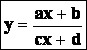
kde c ¹ 0 , ad - cb
¹ 0 . D = R 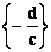 .
.
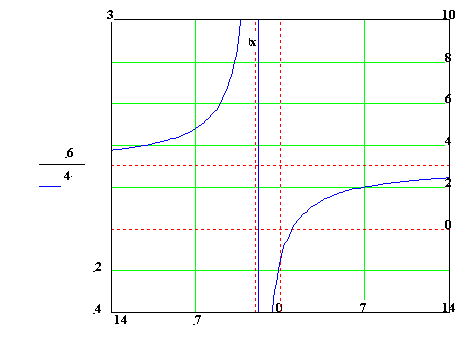
Speciálním případem je funkce y =
![]() tj. nepřímá
úměrnost Jejím grafem
je rovnoosá hyperbola se středem v
bodě S =
tj. nepřímá
úměrnost Jejím grafem
je rovnoosá hyperbola se středem v
bodě S = ![]() ,
asymptotami v osách x a y a osami y
= x. Abychom získali graf funkce
,
asymptotami v osách x a y a osami y
= x. Abychom získali graf funkce ![]() , upravíme pravou stranu rovnice
(dělením) na tvar
, upravíme pravou stranu rovnice
(dělením) na tvar 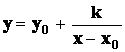 a použijeme transformaci posunutím .
a použijeme transformaci posunutím .
Racionální funkce je daná předpisem
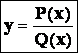
kde P(x) a Q(x) jsou polynomy. D = R ![]()
Iracionální funkce je funkce s nezávisle proměnnou x pod odmocninou.
Uvedeme ty nejjednodušší.
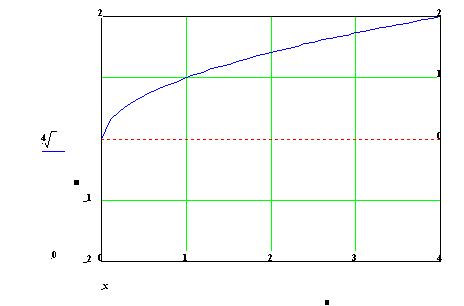
y = ![]() D = H
=
D = H
= ![]() .
Grafem je část paraboly y2 =
x.
.
Grafem je část paraboly y2 =
x.
y = ![]() D = H
= R.
D = H
= R.
y = ![]()
D : 9 - x2 ³ 0 Þ x2 £ 9 x £ 3 Þ xI ñ
H : rovnici umocníme y2 = 9 - x2 Þ x2 + y2 = 9 , tj. kružnice se středem S = ![]() a poloměrem r = Pro naši funkci ale musí
být y ³ 0 , tj. yI
a poloměrem r = Pro naši funkci ale musí
být y ³ 0 , tj. yI![]() . Grafem je horní část kružnice x2 + y2 = 9.
. Grafem je horní část kružnice x2 + y2 = 9.
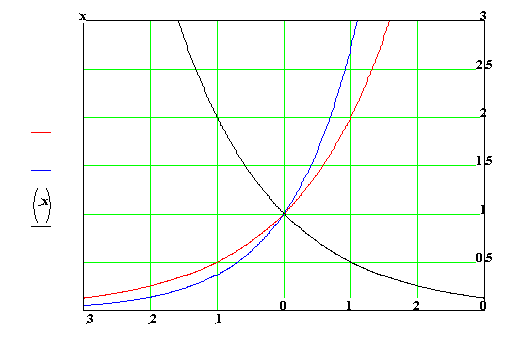
Exponenciální funkce je funkce daná předpisem
![]()
![]()
kde a > 0, a ¹ 1. D = ![]() , H =
, H = ![]() .
V celém definičním oboru je daná funkce prostá.
.
V celém definičním oboru je daná funkce prostá.
Pro a > 1 je ![]() rostoucí, pro a < 1 je
rostoucí, pro a < 1 je ![]() klesající.
klesající.
Grafy :
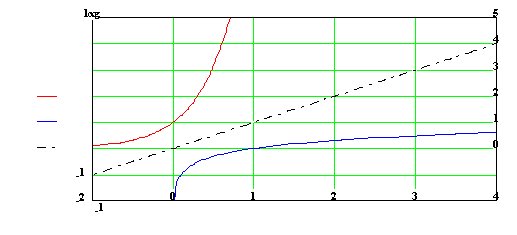
Logaritmické funkce je funkce daná předpisem
![]()
![]()
kde a > 0.
Lze odvodit jako inverzní funkci k funkci exponenciální . Proto
D = ![]() ,
H =
,
H = ![]() .
.
V celém definičním oboru je daná funkce prostá. Graf můžeme sestrojit
jako souměrnou křivku k ![]() vzhledem k přímce y = x.
vzhledem k přímce y = x.
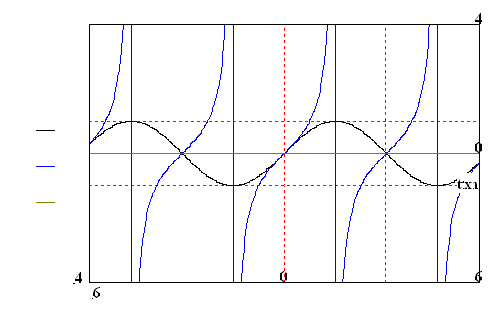
Goniometrické funkce
A.
![]() D =
D = ![]() ,
H =
,
H = ![]()
B.
![]() D =
D = ![]() ,
H =
,
H = ![]()
Funkce y = sin x i y = cos x jsou periodické s periodou 2p
C.
![]() x I
x I ![]() ,
,
![]()
k
- celé číslo, H = ![]()
D.
![]() x I
x I ![]() ,
,
![]()
k
- celé číslo, H = ![]()
Funkce y = tg x a y = cotg x jsou periodické s periodou p
Cyklometrické funkce
Odvodíme je jako inverzní funkce k funkcím goniometrickým.
E.
![]()
Vyjdeme od funkce f : y = sin x a
omezíme se na interval, v němž je funkce prostá, tedy 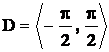 ,
H =
,
H = ![]()
f ‑1 : x = arcsin y a po přeznačení proměnných
y = arcsin x , kde D = ![]() ,
,
 .
.
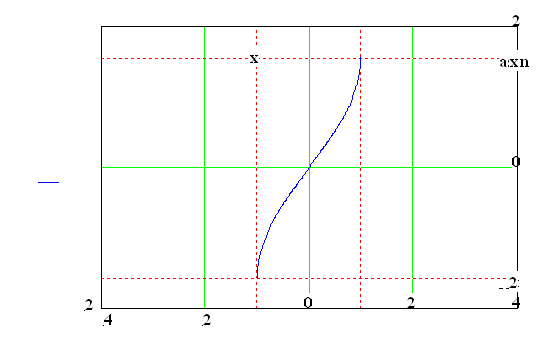
Graf je sestrojen jako souměrně sdružená křivka k funkci
y = sin x pro
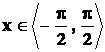 podle přímky y = x .
podle přímky y = x .
F.
![]()
f : y = cos x ![]() ,
H =
,
H = ![]()
f ‑1 : x = arccos y a po přeznačení proměnných
y = arccos x , kde D = ![]() ,
H =
,
H = ![]()
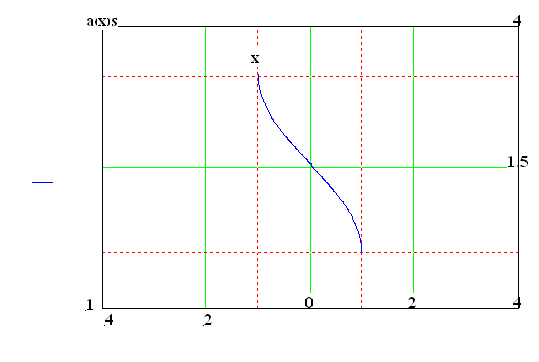
G.
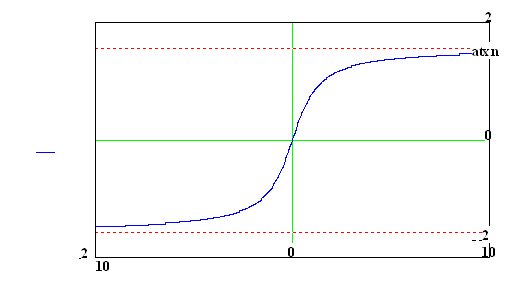
![]()
f : y = tg
x D =![]() ,
H =
,
H = ![]()
f ‑1 : x = arctg y a po přeznačení proměnných
y = arctg x , kde D =![]() ,
H =
,
H = ![]()
H.
![]()
f : y = cotg x D =
![]() ,
H =
,
H = ![]()
f ‑1 : x = arccotg y a po přeznačení proměnných
y = arccotg x , kde D = ![]() ,
H =
,
H = ![]()
Příklad:
Najděte inverzní funkci k funkci y = 2![]() .
.
Řešení ![]()
![]()
D = ![]() ,
funkce je prostá v celém D.
,
funkce je prostá v celém D.
H = ![]() ,
tj. yI
,
tj. yI![]()
Z rovnice y = 2![]() vypočteme x :
vypočteme x :
![]() =
=![]() Û
Û![]() Û
Û![]() Û
Û ![]()
Přeznačíme proměnné f -1 : ![]() pro
xI
pro
xI![]() , y
, y![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1090
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved