Scrigroup - Documente si articole

     

 
HomeDocumenteUploadResurseAlte limbi doc
 
BulgaraCeha slovacaCroataEnglezaEstonaFinlandezaFranceza
GermanaItalianaLetonaLituanianaMaghiaraOlandezaPoloneza
SarbaSlovenaSpaniolaSuedezaTurcaUcraineana

BiologieBudovaChemieEkologieEkonomieElektřinaFinanceFyzikální
GramatikaHistorieHudbaJídloKnihyKomunikaceKosmetikaLékařství
LiteraturaManagementMarketingMatematikaObchodPočítačůPolitikaPrávo
PsychologieRůznéReceptySociologieSportSprávaTechnikaúčetní
VzděláníZemědělstvíZeměpisžurnalistika

INVERZNÍ MATICE

matematika



+ Font mai mare | - Font mai mic



DOCUMENTE SIMILARE

TERMENI importanti pentru acest document

Inverzní matice

Definice: Pokud =0, potom čtvercovou matici A nazveme singulární. V opačném případě nazveme regulární.

Definice: Matici X nazveme maticí inverzní k regulární matici A, jestliže platí :

A.X = X.A = E

Označíme

X = A

Definice: Matici nazveme adjungovanou k čtvercové matici A, jestliže každý prvek aik nahradíme jeho algebraickým doplňkem Dik a takto vzniklou matici transponujeme.



==

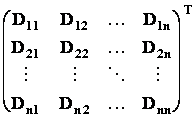Věta: (výpočet inverzní matice)

Buď A regulární matice. Pak

A  =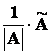

Příklad: Určete matici inverzní k matici A

A =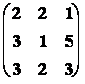 

Řešení : = 1 ¹ 0, čili A je regulární a A existuje.

===

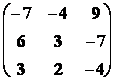
A  ==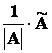 

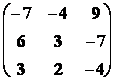
Zkouška : A. A 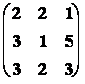 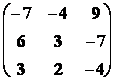=. ==E


Politica de confidentialitate | Termeni si conditii de utilizare



DISTRIBUIE DOCUMENTUL

Comentarii


Vizualizari: 817
Importanta: rank

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved