| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
8.1. Kombinatorika
Přehled vzorců:
Permutace (bez opakování) – uspořádané n–tice z daných n prvků (skupiny, které obsahují všechny dané prvky a liší se pouze jejich pořadím).
Počet permutací z n prvků: P(n) = n! (čteme n – faktoriál)
n! = n(n–1)(n–2) .3.2.1
Definitoricky:
Variace k–té třídy z n různých prvků (bez opakování) – uspořádané skupiny o k prvcích z daných n prvků, přičemž každý prvek se vyskytuje jen jednou.
Počet
variací k–té třídy z n prvků: V(k, n) = ![]()
Kombinace k–té třídy z n různých prvků (bez opakování) – skupiny k prvků vybraných z n prvků bez ohledu na jejich uspořádání, ve kterých se každý prvek vyskytuje jen jednou.
Počet
kombinací k–té třídy z n prvků: K(k,
n) =![]() =
= ![]()
![]() – tzv. kombinační číslo (binomický
koeficient), výraz čteme: n nad k.
– tzv. kombinační číslo (binomický
koeficient), výraz čteme: n nad k.
Pro kombinační číslo ![]() , 0 k n, platí:
, 0 k n, platí:
1. ![]() = n ;
= n ; ![]() =
= ![]() = 1 ;
= 1 ; ![]() = 1;
= 1;
![]() =
= ![]()
![]() =
= ![]() ;
;
![]() +
+ ![]() =
= ![]()
Binomická věta
Pro libovolná reálná (komplexní) čísla a, b a pro libovolné přirozené číslo n platí:
(a + b)n
= ![]() =
= ![]()
Kombinační čísla ![]() se nazývají binomické
koeficienty.
se nazývají binomické
koeficienty.
Pro (k+1) – ní člen binomického
rozvoje platí: Ak+1 = ![]() , 0 k n.
, 0 k n.
Pascalův trojúhelník – je schéma kombinačních čísel, které můžeme zapsat takto: krajní čísla jsou 1 a každé další číslo se rovná součtu čísel bezprostředně nad ním.
Pro:
n = 0 ![]() 1
1
n = 1 ![]()
![]() 1 1
1 1
n = 2 ![]()
![]()
![]() 1 2 1
1 2 1
n = 3 ![]()
![]()
![]()
![]() 1 3 3 1
1 3 3 1
n = 4 ![]()
![]()
![]()
![]()
![]() 1 4 6 4 1
1 4 6 4 1
Čísla v jednom řádku Pascalova trojúhelníka jsou koeficienty rozvoje (a + b)n pro odpovídající n.
Např. n = 3 (a + b) a a b + 3 ab b
8.2. Pravděpodobnost
Náhodný pokus – výsledek nelze předem určit, přitom jednotlivé možnosti výsledku se navzájem vylučují a jedna z nich nastane vždy. Množinu všech možných výsledků (elementárních jevů) značíme W a libovolný její prvek w
Podmnožiny množiny W nazýváme jevy a značíme A, B, C. . . Prvkům jevu A říkáme výsledky příznivé jevu A.
Jev nemožný značíme symbolem (prázdná množina), jev jistý W
Každému výsledku w I W je
přiřazena pravděpodobnost p(w).
Pravděpodobnosti p(w) jsou nezáporná čísla, jejichž součet je
roven jedné: ![]() =
=
Má-li
množina W m
prvků a jsme-li přesvědčeni, že jsou stejně
pravděpodobné, položíme p(w ![]() pro všechna w I W
pro všechna w I W
Pravděpodobnost jevu A značíme P(A). Definuje se jako součet
pravděpodobností výsledků příznivých jevu A, tj. P(A) = ![]() .
.
V pokusu, který má m
stejně pravděpodobných výsledků, se pravděpodobnost jevu
rovná počtu výsledků příznivých dělenému počtem všech výsledků
možných: P(A) =![]()
Základní vlastnosti pravděpodobnosti
Pro pravděpodobnost libovolného
jevu A platí ![]() .
.
Pravděpodobnost jistého jevu je rovna jedné P(W
Pravděpodobnost nemožného jevu je rovna nule P(
Pravděpodobnost
opačného jevu je doplněk pravděpodobnosti výchozího jevu do
jedné P(A´)
= 1 – P(A).
Sjednocení A B znamená, že nastává aspoň jeden z jevů A, B.
Průnik A B znamená, že nastávají oba jevy, A i B.
A´ znamená opačný jev k jevu A, tj. jev, který nastává právě tehdy, nenastane-li jev A.
Pokud se jevy A a B navzájem vylučují, (A B = ), pak pravděpodobnost jejich sjednocení P(A B) = P(A) + P(B) (sčítání pravděpodobností). Totéž platí pro větší počet jevů.
Obecně je ovšem P(A B) = P(A) + P(B) – P(A B).
Pro neslučitelné jevy platí: P(A B) = P(A) P(B) (násobení pravděpodobností).
Řešené příklady
Příklad 1
Pro přípustné hodnoty upravte
výraz ![]() .
.
Řešení.
Za předpokladu n 2 je:
![]() =
= ![]() = n(n –.1) – n(n –1) = 0.
= n(n –.1) – n(n –1) = 0.
Příklad 2.
Kolika způsoby můžeme spojit 10 bodů, jestliže 3 z nich leží na jedné přímce.
Řešení.
Deset bodů určuje K(2, 10) přímek, jestliže žádné 3 body neleží na jedné přímce. Tři body by určovaly K(2, 3) přímek, v našem zadání jen jednu. Celkový počet přímek:
K(2, 10) – K(2, 3) + 1 = 43.
Příklad 3.
Pro jaké x v rozvoji výrazu (x –i ![]() )10 se
sedmý člen rozvoje rovná –105?
)10 se
sedmý člen rozvoje rovná –105?
Řešení.
Sedmý člen A7 = ![]() .
.
Dále řešíme rovnici ![]() = –105
= –105
![]() . Po úpravách 210 x4
= 105
. Po úpravách 210 x4
= 105
![]() T x =
T x = ![]() .
.
Příklad 4.
Ve třídě je 12 chlapců a 5 dívek. Kolika způsoby lze mezi nimi vybrat 3 zástupce tak, aby mezi vybranými zástupci byly:
a) samé dívky, b) právě dvě dívky, c) nejvýše dvě dívky
Řešení.
a)
Vybíráme pouze z dívek,
nezáleží na pořadí, použijeme K(3, 5) = ![]()
![]() = 10
= 10
b) Z 5 dívek vybíráme dvě a z 12 chlapců jednoho. Všech možností výběru je
![]()
![]() = 10
= 10
c) Mají-li být zastoupeni nejvýše dvě
dívky, tj. nebude tam žádná, bude jedna nebo dvě. Počet všech
možností je tedy ![]() = 220 + 5
= 220 + 5
Úlohy k řešení
Zvětší-li se počet
prvků o dva, zvětší se počet permutací (bez opakování)
dvacetkrát. Kolik bylo prvků?
[ n = 3]
Kolik čtyřciferných
čísel lze sestavit z číslic 1, 2, 3, 4, 5, jestliže se v napsaném
čísle žádná číslice neopakuje?
[ 120 ]
Kolik různých dvouciferných
čísel je možno sestavit z číslic 1, 2, 3, 4, 5, když se nemá ani v
jednom čísle žádná číslice opakovat?
[ V(2, 5) = 20 ]
Z kolika prvků je možno
vytvořit 420 variací druhé třídy bez opakování?
[ n = 21 ]
Zmenšíme-li počet prvků
určité množiny o dva, zmenší se počet všech jejich permutací
dvacetkrát. Určete původní počet prvků.
[ n = 5 ]
Dokažte:
a) n! + n2 (n – l) ! = (n +
l) !
b) (n + l) ! – n ! = n .n !
[ Po rozepsání levé strany : a) n! +
n.n.(n–l)! = n! + n.n! = (n+1).n! = (n+1)!
b)
(n+l)n! – n! = n!(n + l – l) = n .n! ]
Zjednodušte:
a) ![]() , b)
, b) ![]() ,
,
c) ![]()
[ a) 1, b)
2, c)
0 ]
Vyjádřete jedním
kombinačním číslem:
a) ![]() , b)
, b) ![]() , c)
, c) ![]() ,
,
d) ![]() , e)
, e) ![]()
[ a) ![]() , b)
, b) ![]() , c)
, c)
![]() , d)
, d) ![]() , e)
, e) ![]() ]
]
Řešte rovnice v R a proveďte
zkoušku:
a) ![]() , b)
, b)
![]() +
+![]() = 4 c)
= 4 c) ![]() = 4,
= 4,
d) x! = 210(x – 2)! e)
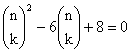
[ a) x = 4 b) x
= 4, c) x = 4, d) x = 15,
e) (n = 4 k
= 1) (n
= 4 k=
3) (n
= 2 k
= 1)![]() ]
]
V oboru
komplexních čísel řešte rovnice:
a) (1 – 2i)z = 2![]() – i(2 + i), b) z2 = z +
– i(2 + i), b) z2 = z + ![]() , c)
z +
, c)
z + ![]() = z z
= z z
a)
z = 7 + 4i, b)
z = 0 z
= 2, c) z = 0 z
= –2 z
= 2
Určete,
který člen binomického rozvoje 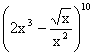 obsahuje x3.
obsahuje x3.
sedmý člen
Kolik
různých tříciferných čísel lze utvořit pomocí číslic
dělitelných třemi, nemá-li se žádná číslice opakovat?
[ 3! = 6 ]
Kolik
trojzvuků je možno utvořit z 8 tónů?
[![]() = 56 ]
= 56 ]
Kolika
způsoby je možno vytáhnout 4 karty z 32 karet?
[![]() = 35 960 ]
= 35 960 ]
Kolik
je možných tipů ve Sportce, když tipujeme na každém tiketu jako jedno ze
šesti čísel trojku? (V osudí je vloženo celkem 49 míčků,
očíslovaných od l do 49.)
[![]() = 1 712 304 ]
= 1 712 304 ]
Kolik
přímek je určeno 8 body v rovině, z nichž žádné 3 neleží v jedné
přímce?
[![]() = 28 ]
= 28 ]
Náhodně sestavíme trojciferné číslo z číslic l,2,3. Jaká
je pravděpodobnost, že vzniklé číslo je větší než 300?
[ 1/3 ]
Jaká
je pravděpodobnost, že při dvou hodech pravidelnou hrací kostkou
nepadne ani jedna šestka?
[ (5/6)2 ]
Jaká
je pravděpodobnost, že přirozené číslo, náhodně vybrané z
čísel l až 50 není dělitelné pěti?
[ A - náhodně vybrané přirozené číslo z čísel 1 až 50 není
dělitelné pěti
![]() - opačný jev k
jevu A , P(
- opačný jev k
jevu A , P(![]() ) =
) = ![]() P(A) = 1 – P(
P(A) = 1 – P(![]() ) = 0,8 ]
) = 0,8 ]
Házíme
dvakrát hrací kostkou. S jakou pravděpodobností součet bodů z
těchto dvou hodů bude větší než 7?
[ P = 15/36 = 5/12 = 0,416 ]
V
osudí je 10 koulí stejné velikosti, z
nichž jsou 4 bílé a 6 červených.Náhodně vybereme
3. S jakou pravděpodobností je alespoň jedna bílá?
[ A - alespoň jedna vybraná koule je bílá, ![]() - žádná vybraná koule
není bílá
- žádná vybraná koule
není bílá
P(![]() ) =
) = ![]() , P(A)
= 1 – P(
, P(A)
= 1 – P(![]() ) =
) = ![]() ]
]
Jaká
je pravděpodobnost, že při hodu dvěmi kostkami
a) padne součet 10 ? b)
padnou jen lichá čísla ?
[ a) 1/12, b) 1/4 ]
Sklad
zásobuje 10 prodejen. Rozvoz zboží se vždy uskutečňuje třemi jízdami. Při první jízdě mají
být zásobeny prodejny 1 - 5 (v libovolném pořadí), při druhé
jízdě prodejny 6 - 8 (v libovolném pořadí) a při třetí
jízdě prodejny 9 a 10, opět v libovolném pořadí. Kolik je
různých pořadí dodávek za těchto podmínek?
[ 5!3!2! = 1440 ]
V
krabici je 16 výrobků bezvadných a 4 vadné. Kolikerým způsobem lze
při náhodném výběru 5 kusů vybrat:
a) pouze bezvadné výrobky,
b) 4 výrobky bezvadné, 1 vadný ,
c) 4 výrobky vadné, 1 bezvadný.
[ a) ![]() , b)
, b) ![]() , c)
, c) ![]() ]
]
V
dostihu běží 5 koní. Kolika
způsoby mohou být obsazena první tři místa v cíli?
(Předpokládáme, že na tomtéž místě nemohou současně
doběhnout dva koně.)
[ 60 způsobů ]
Pomocí
binomické věty určete:
a) 3. člen rozvoje ( 1 + i )7
, b) 20. člen
rozvoje (1 + i)35
[ a) A3 = –![]() = –21, b)
A20 = –i
= –21, b)
A20 = –i![]() ]
]
S
jakou pravděpodobností při hodu třemi kostkami padnou samé šestky?
[ (1/6)3]
Jaká
je pravděpodobnost, že náhodně vybrané telefonní číslo končí trojkou?
[ 1/10]
Jaká
je pravděpodobnost, že libovolné přirozené číslo
začíná lichou číslicí?
[ 1/2 ]
Pro
jaké x v rozvoji výrazu (x –![]() )9 se
třetí člen rozvoje rovná –108?
)9 se
třetí člen rozvoje rovná –108?
[ x = –1]
S
jakou pravděpodobností při
šesti hodech hrací kostkou padnou pouze
lichá čísla?
[ P = 0,016]
Házím
desetkrát hrací kostkou. S jakou pravděpodobností
a) šestka nepadne ani jednou , b)
šestka padne alespoň jednou.
[ a) P = 0,162, b) P = 0,838 ]
Test č. 8
U každé úlohy je právě 1 odpověď správná.
|
1. Součet a) e) žádná z uvedených odpovědí není právná. |
|
Úpravou výrazu a) 1, b) –1, c) n! , d) (n – 1)!, e) žádná z uvedených odpovědí není právná. |
|
Pro která přirozená čísla n
platí (i) a) n = 5 , b) n = 6 , c) n = 4 , d) n = 6 nebo n = 2 , (ii) e) žádná z uvedených odpovědí není právná. |
|
4. Zmenší-li se počet prvků o 2, zmenší se počet permutací těchto prvků 20x. Kolik je prvků? a) 6 , b) 7 , c) 5 , d) 8 , e) žádná z uvedených odpovědí není právná. |
|
5. V binomickém rozvoji a) šestý , b) neexistuje , c) pátý , d) čtvrtý , e) žádná z uvedených odpovědí není právná. |
|
6. Hodíme najednou červenou a zelenou hrací kostkou. Pravděpodobnost, že padne šestka pouze na zelené kostce je: a) 1/36 , b) 5/36 , c) 6/36 , d) 10/36 , e) žádná z uvedených odpovědí není právná. |
|
7. Kolik různých trikolor můžeme sestavit z pěti různých barev: a) deset , b) šedesát , c) třicet , d) dvacet , e) žádná z uvedených odpovědí není právná. |
|
8. Kolik prvků je třeba vzít, aby z nich bylo možno utvořit šestkrát více kombinací čtvrté třídy než kombinací druhé třídy: a) 11, b) 10, c) 12, d) 13, e) žádná z uvedených odpovědí není právná. |
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1925
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved