| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Definice: Okolím
reálného čísla a nazýváme
otevřený interval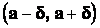 
,
kde d je libovolné kladné číslo („delta okolí“).
Je to tedy množina reálných čísel x,
které vyhovují nerovnostem 
,
neboli 
.
Geometricky značí okolí bodu a úsečku délky 2d, se středem v bodě a. číslo d se někdy nazývá poloměr okolí. Krajní body úsečky a + d, a ‑ d k úsečce nepatří
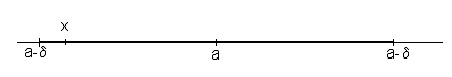
Jestliže množinu reálných čísel rozšíříme i o nevlastní čísla +¥ ¥, pak můžeme analogicky definovat také okolí těchto nevlastních bodů.
Okolí čísla +¥ nazveme interval (K, ¥), tj. množinu všech bodů, pro něž platí x > K a podobně okolím čísla ‑¥ bude interval (‑¥, K), tj. množina všech bodů, pro něž platí x < K.
Poznámka: Zavedené „delta okolí“ bodu a značíme někdy Ud(a), resp. zkráceně Ud. Analogicky okolí bodu +¥, resp. ‑¥, můžeme značit UK(+¥), resp. UK(‑¥
Definice: Číslo A se nazývá limitou funkce f v bodě
a, jestliže ke každému
libovolnému e > 0 existuje okolí
bodu a
takové, že pro každou hodnotu argumentu x I Ud(a), x ¹ a, je splněna nerovnost 
.
Zápis :
tak, že 
Þ
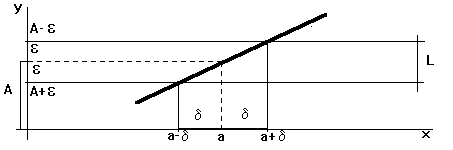
Geometrický význam
Splnění nerovnosti
tedy 
pro jakkoliv malé e < 0
znamená, že hodnoty funkce f(x) pro ta x, která leží v okolí bodu a, tedy pro něž platí ,
musí ležet v pásu L šířky 2e , tj. v intervalu 
.
Jaká je hodnota funkce v bodě a, nebo
zda vůbec existuje, přitom nezáleží.
Definice zůstává v platnosti i pro případ, že x ¥, resp. x ¥
tak, že 
je ,
tzn. že ke každému libovolnému e > 0 musí existovat číslo K tak, aby pro
všechna x > K platila nerovnost
a
tak, že 
je ,
tzn. že ke každému libovolnému e > 0 musí existovat číslo K tak, aby pro
všechna x < K platila nerovnost
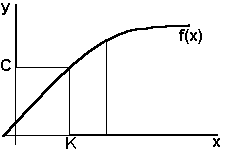
Geometrická interpretace 
je na obrázku.
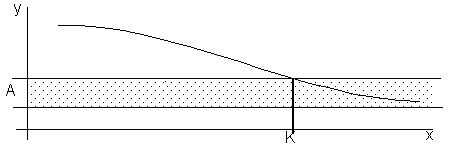
Splnění nerovnosti
pro jakkoliv malé e > 0
znamená, že funkční hodnoty f(x) pro všechna
x > K musí ležet v pásu šířky 2e, v intervalu .
Definice: Funkce f(x) má v bodě a nevlastní limitu +¥, když ke každému zvolenému číslu C existuje okolí Ud(a) takové, že pro každé x I Ud(a), x ¹ a, je splněna nerovnost f(x) > C.
Zápis :
tak, že pro 
resp. (pro ¥
tak, že pro 
Geometrická interpretace
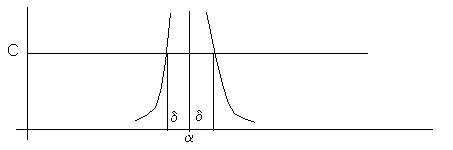
Funkce může mít nevlastní limitu i v případě, že x ¥, resp. x ¥
tak, že pro x > K Þ f(x) > C
tak, že pro x > K Þ f(x) < C
tak, že pro x < K Þ f(x) > C
tak, že pro x < K Þ f(x) < C
Geometrická interpretace
Často potřebujeme vyšetřovat, resp. dokazovat
limity funkcí, pokud x volíme v
levém okolí
bodu a, Ud (a), tj. volíme ta x, pro něž platí a ‑ d < x < a, resp. v pravém okolí bodu a, Ud (a), tj.
volíme ta x, pro něž platí
a < x < a + d. Těmto limitám říkáme „limita zleva“, značíme ji 
,
resp. „limita
zprava“,
značíme ji 
.
Jednostranné limity mohou být buď vlastní (tzn. konečná čísla) nebo nevlastní (tzn. buď +¥ nebo ‑¥). Platí
Û 
= 
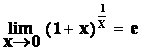
Hodnotu limity vypočteme přímo
použitím vět o limitách. Např.
Při výpočtu limity zlomku 
dospíváme často k výrazu:
typu „
“.
Hodnotu limity přímo nelze určit. Úpravu provádíme tak, že se snažíme zlomek
zkrátit výrazem konvergujícím k nule. Např.
A)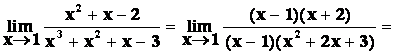 
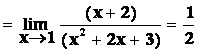
B)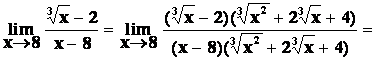 
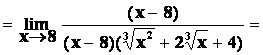
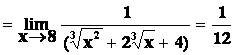
typu „
“.
Zde se jedná o limitu nevlastní. Její existenci a určení provedeme výpočtem
obou jednostranných limit. Např.
A) 
(výraz „
“).
Zda tato nevlastní limita existuje, rozhodneme výpočtem obou jednostranných
limit
,
Þ
nevlastní limita neex.
Použijeme známých limit. Např.
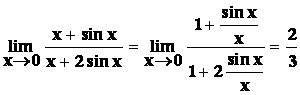
Limitu v ¥ určujeme podobně jako limitu posloupnosti. Např.
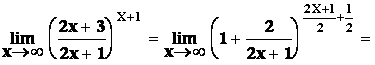
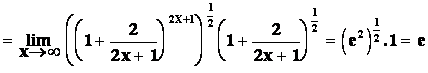
Když jsme vyšetřovali existenci limity funkce f v bodě a, nemusela být hodnota funkce f(a) vůbec definovaná. Chceme‑li vyšetřovat spojitost funkce v bodě a, bude mít hodnota f(a) důležitý význam.
Definice: Funkce f je spojitá v bodě a, jestliže v tomto bodě má limitu a ta se rovná funkční hodnotě f(a), tedy
Např. funkce f(x) =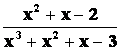
v bodě 1 má konečnou limitu,
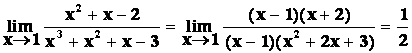
Ale f(x) v bodě 1 není definovaná („“)
a proto funkce f(x) v bodě 1 není
spojitá.
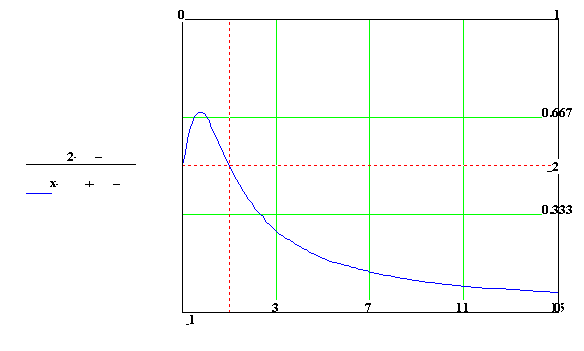
Poznámka1: Body nespojitosti dělíme na tři druhy :
Odstranitelná nespojitost: Existuje konečná limita v bodě, ale funkce není v něm definovaná.
Konečný skok: Obě dvě jednostranné limity jsou konečné a různé.
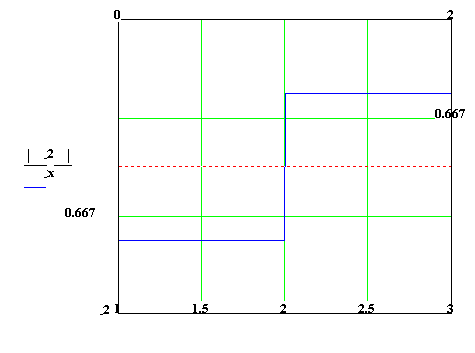
Nekonečný skok: Aspoň jedna z jednostranných limit je nevlastní nebo neexistuje.
Poznámka2: Je‑li funkce spojitá v každém bodě intervalu (a,b), nazýváme ji spojitou funkcí v otevřeném intervalu (a,b) . V případě, že se jedná o interval uzavřený <a,b>, musí být funkce spojitá ve všech vnitřních bodech, v bodě a spojitá zprava a v bodě b spojitá zleva.
Některé důležité věty:
Věta : Nechť funkce f je spojitá v uzavřeném intervalu <a,b> a nechť čísla f(a), f(b) mají různá znaménka, tj. f(a).f(b) < 0. Pak existuje takové číslo cI(a,b), že f(c) = 0.
Věta : (1. věta Weierstrassova : o omezenosti funkce)
Jestliže funkce f je v uzavřeném intervalu <a,b> spojitá , pak je v tomto intervalu ohraničená.
V předpokladu této věty je podstatné, že funkce
je spojitá ve všech bodech uzavřeného intervalu <a,b>. Např. funkce 
je spojitá v intervalu (0,1> a je v (0,1> neomezená.
Věta : (2. věta Weierstrassova : o maximu a minimu funkce)
Jestliže funkce f je v uzavřeném intervalu <a,b> spojitá , pak existuje v tomto intervalu aspoň jeden bod C1 , ve kterém funkce f nabývá své největší hodnoty, a aspoň jeden bod C2 , ve kterém funkce f nabývá své nejmenší hodnoty.
V předpokladu této věty je opět podstatné, že
funkce je spojitá ve všech bodech uzavřeného intervalu <a,b>. Např. funkce je spojitá v intervalu (0,1> ale maximum zde nemá.
Věta : (Bolzanova)
Funkce f spojitá v uzavřeném intervalu <a,b> , nabývá všech hodnot mezi čísly f(a), f(b).
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 870
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved
