| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Logicko - kombinatorické metódy.
1. Princíp vypojenia a zapojenia.
Veta 1.1.
Nech M1 .. Mn
sú konečné množiny. Pre 'kI1..n : Sk=![]() . Potom
. Potom ![]() =
=![]() .
.
Dôkaz.
Nech xI![]() patrí do m
množín. Koľko krát je x zarátaný
do
patrí do m
množín. Koľko krát je x zarátaný
do ![]() ? Do S1
m-krát, do Si
? Do S1
m-krát, do Si ![]() -krát, do
-krát, do ![]() 2m-krát a teda do
2m-krát a teda do ![]()
![]() = 1-krát. Tým je tvrdenie
dokázané.
= 1-krát. Tým je tvrdenie
dokázané.
Veta 1.2.
Nech ![]() je množina
surjekcií z A do B, |A|=m a B = . Potom
je množina
surjekcií z A do B, |A|=m a B = . Potom ![]() =
=![]()
Dôkaz.
Od všetkých odpočítame
nesurjekcie. Označme M(k) množinu funkcií z A do B,
ktoré žiaden prvok A nezobrazia na bk. Je zrejmé, že |M(i1,
.. , ik)| = (n - k)m. Potom
Sk = ![]() .(n - k)m a použitím formule
vypojenia a zapojenia dostávam presne to, čo potrebujem.
.(n - k)m a použitím formule
vypojenia a zapojenia dostávam presne to, čo potrebujem.
Označenie.
Pre systém množín M1 .. Mn budeme M(r) označovať počet prvkov, ktoré patria práve do r množín a M´(r) počet prvkov, ktoré patria aspoň do r množín.
Veta 1.3.
Nech M1 .. Mn
sú konečné množiny. Potom M(r) =![]() , kde Sk=
, kde Sk=![]() .
.
Dôkaz.
Prvok z r množín dáva vklad 1 podľa vety 1.1.
Prvky z menej množín nedávajú vklad, lebo kombinačné číslo v sume je
pre ne nula. Potrebujeme ešte dokázať, že prvky z viac množín tiež
nedávajú vklad. nech x patrí do s > r množín. Potom x dáva
vklad ![]() , pričom
, pričom ![]() =
= ![]() =
=![]() =
=![]() , takže
, takže ![]() =
=![]() =
= ![]() = (j = k-r) =
= (j = k-r) =![]() = 0 podľa vety 3.1.3.1
odsek 7.
= 0 podľa vety 3.1.3.1
odsek 7.
Veta 1.4.
Nech M1 .. Mn
sú konečné množiny. Potom M´(r) =![]() , kde Sk=
, kde Sk=![]() .
.
Dôkaz.
M´(r) =![]() =
=![]() =
=![]() = (j=k-i) =
= (j=k-i) =![]() =
=![]() =
=![]() =
=![]() .
.
2. Spernerova veta.
Veta 2.1.
Nech A1 .. An
sú podmnožiny A, z ktorých žiadna nie
je podmnožinou inej. Potom 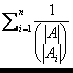 Ł 1.
Ł 1.
Dôkaz.
Uvažujme reťazec Ć=C0ĚC1Ě .. ĚCm=A, kde |A| = m. Takýchto reťazcov existuje m! (každý reťazec určuje permutáciu A). Ak $iI1..m $jI1..n : Ci=Aj, hovoríme, že reťazec prechádza množinou Aj.
Zároveň keďže A1
.. An sú do seba
nezapadajúce, žiadny reťazec neprechádza viac ako jednou z nich. Ak |Aj| = rj, tak množinou Aj
prechádza rj!(n-rj)!
reťazcov (rj! vchádza
a (n-rj)! vychádza). Ale
suma reťazcov, prechádzajúcich cez množiny A1 .. An
musí byť menšia ako m!, takže 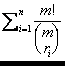 Ł m!, čo tvrdenie dokazuje.
Ł m!, čo tvrdenie dokazuje.
Veta 2.2 (Sperner).
Nech |A| = n a A1 .. Am sú konečné neprázdne
podmnožiny A, z ktorých žiadna nie je
podmnožinou inej. Potom m Ł![]() .
.
Dôkaz.
Stačí pre iI1..n odhadnúť |Ai|»![]() a použiť predchádzajúcu vetu.
a použiť predchádzajúcu vetu. 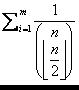 =
=![]() Ł 1 Ű m Ł
Ł 1 Ű m Ł![]() .
.
3. Dirichletov princíp.
Veta 3.1.
Nech A,B sú množiny a f : A®B zobrazenie. Ak |A| > |B|, tak $x,yIA : f(x) = f(y).
Dôkaz.
Triviálne.
Dôsledok 3.1.
Nech A,B sú množiny a f : A®B zobrazenie. Ak |A| > k.|B|, tak $x1..xk+1IA 'i,jI1..k+1 : f(xi) = f(xj).
Dôkaz.
Triviálne.
Dôsledok
Nech A,B sú množiny a f : A®B zobrazenie. Ak A je nekonečná a B je konečná, tak $yIB : f-1(y) = je nekonečná.
Dôkaz.
Triviálne.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 915
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved