| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
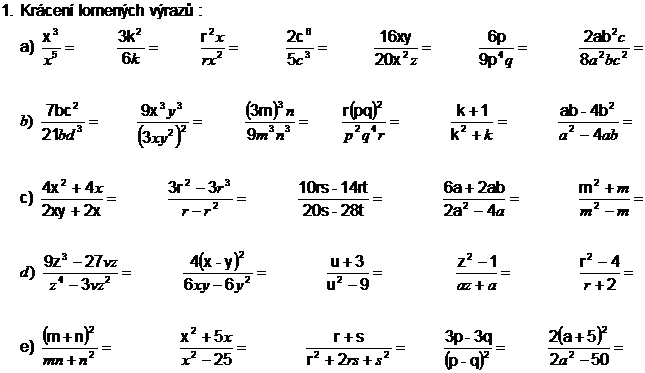
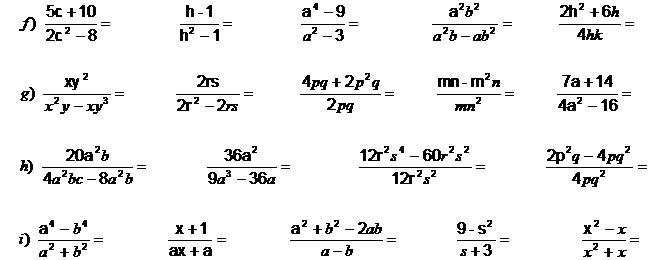
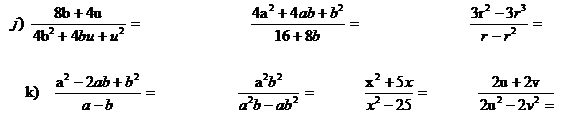
l) ![]()
m) ![]()
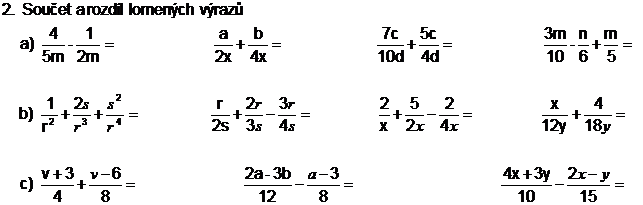
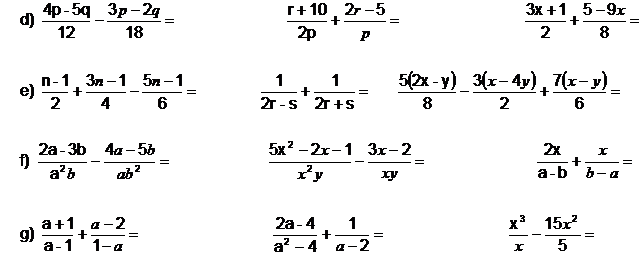
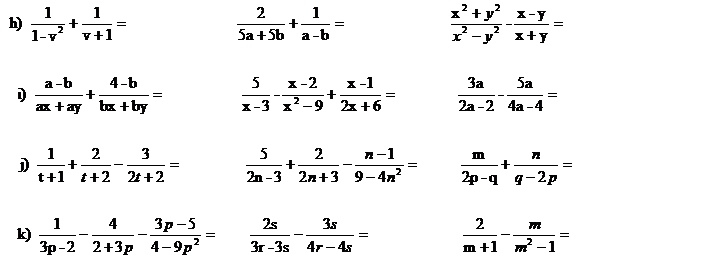
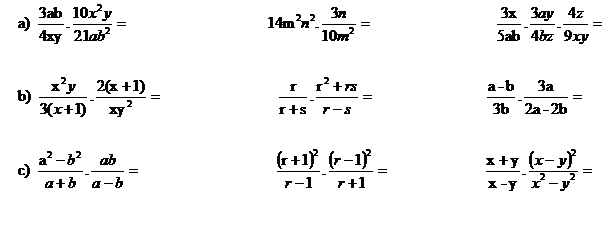
![]()
m) ![]()
![]()
![]()
Součin čitatelů lomíme součinem jmenovatelů.
![]()
![]()
Čitatele krátíme se jmenovatelem.
![]()
![]() a a
a a
Postup při násobení lomených výrazů
Čitatele i jmenovatele rozložíme na součin ( vytýkáním, pomocí vzorců )
Čitatele vykrátíme se jmenovateli
Součin čitatelů lomíme součinem jmenovatelů
Uvedeme podmínky řešitelnosti
Př.:
![]()
n n
Vypočítej a uveď podmínky řešitelnosti:
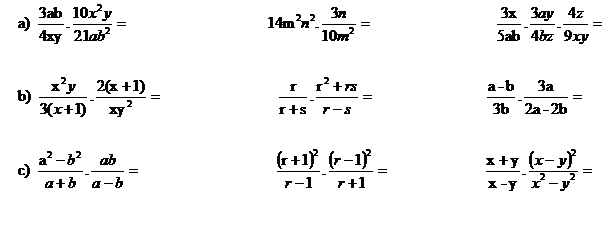
![]()
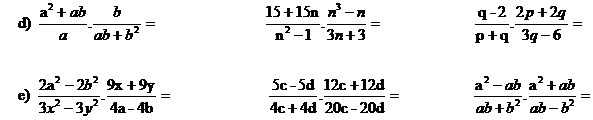
![]()
![]()
Rozšiřování zlomků
Čitatele i jmenovatele násobíme
stejným číslem různým od nuly. Hodnota zlomku se nemění.
![]()
Krácení zlomků
Čitatele i jmenovatele dělíme
stejným číslem různým od nuly. Hodnota zlomku se nemění.
![]()
Násobení zlomků
a)
Zlomek násobíme
celým číslem tak, že celým číslem vynásobíme čitatele a jmenovatele opíšeme. Hodnota zlomku se
mění. b)
Zlomek násobíme
zlomkem tak, že součin čitatelů lomíme součinem
jmenovatelů. c)
![]()
![]() Hodnota zlomku se mění.
Hodnota zlomku se mění.
Dělení zlomků
Vydělit číslo daným číslem
znamená vlastně vynásobit číslo převrácenou hodnotou daného
čísla.
![]()
![]()
4. Dělení lomených výrazů
a) ![]()
![]()
![]()
![]()
b) ![]()
![]()
![]()
c) ![]()
![]()
![]()
d) ![]()
![]()
![]()
e) ![]()
![]()
![]()
f) 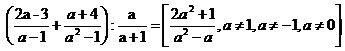
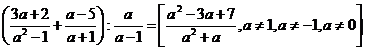
Složené lomené výrazy
Složený výraz vypočítáme, jestliže
součin vnějších členů lomíme součinem
vnitřních členů.
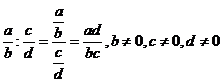
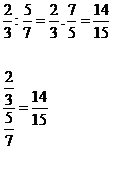
Příklad:
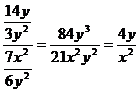
Krácení složených lomených výrazů
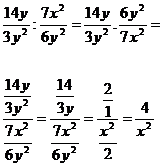
Jakýkoliv vnější člen můžeme krátit s jakýmkoliv vnitřním členem.
Procvičování
a) ![]()
![]()
b) ![]()
![]()
c) 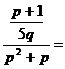
![]()
d) ![]()
![]()
e) 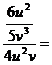
![]()
f) ![]()
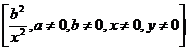
g) 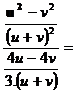
![]()
Ukázkové příklady:
![]()
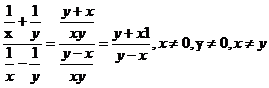
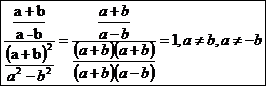
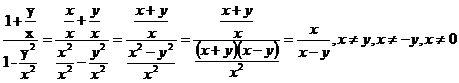
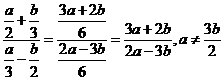
1. Vypočítej a uveď podmínky řešitelnosti:
a) 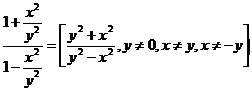
b) 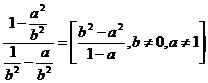
c) 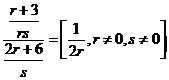
d) 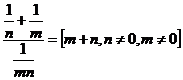
e) 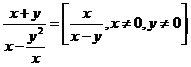
f) 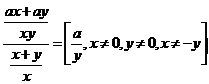
g) 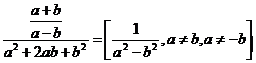
h) 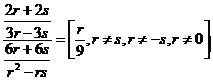
i)
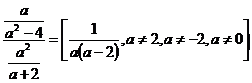
2. Vypočítej a uveď podmínky řešitelnosti:
a)
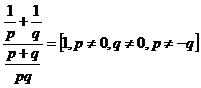
b)
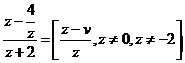
c)
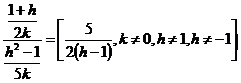
d)
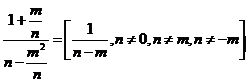
e)
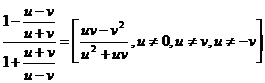
3. Vypočítej a uveď podmínky řešitelnosti:
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
f)
![]()
g)
![]()
h)
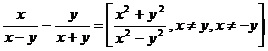
i)
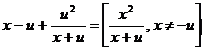
4. Vypočítej a uveď podmínky řešitelnosti:
a)
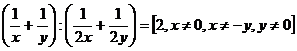
b)
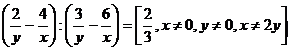
c)
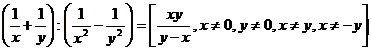
d)
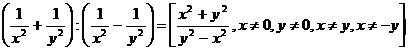
5. Vypočítej, stanov podmínky řešitelnosti a výpočet ověř pro x = 2
a)
![]()
b)
![]()
c)
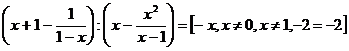
d)
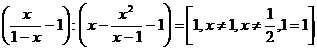
Vypočítej a stanov podmínky řešitelnosti:
a)
![]()
b)
![]()
c)
![]()
d)
![]()
Vyhledej nejmenší společný násobek výrazů:
![]()
Převeď na společného jmenovatele zlomky:
![]()
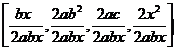
Vykrať zlomky a uveď podmínky řešitelnosti:
a)
![]()
b)
![]()
Vypočítej, urči podmínky řešitelnosti:
a)
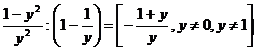
b)
![]()
Vykrať a urči podmínky řešitelnosti:
a)
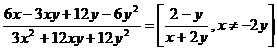
b) 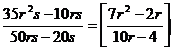
c)
![]()
d)
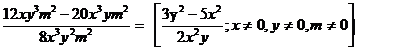
e) ![]()
f)
![]()
Vypočítej:
a)
![]()
b)
![]()
c)
![]()
Převeď na společného jmenovatele zlomky:
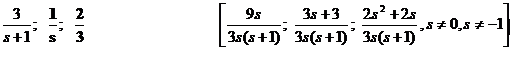
Urči podmínky řešitelnosti:
a)
![]()
b)
![]()
Vypočítej a stanov podmínky řešitelnosti:
a)
![]()
b)
![]()
Vypočítej, stanov podmínky řešitelnosti:
a)
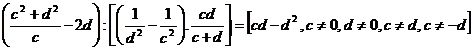
b)
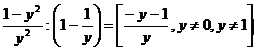
c)
![]()
d)
![]()
Elektrický odpor R drátu délky l a průřezu S při měrném odporu r je vyjádřen vzorcem
![]() Vyjádři
z tohoto vzorce l.
Vyjádři
z tohoto vzorce l.
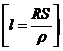
Pro napětí U a odpor
vodičů R spojených sériově platí: ![]() Vyjádři velikost
U2.
Vyjádři velikost
U2.
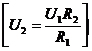
Rovnice s neznámou ve jmenovateli
Postup při výpočtu:
I. Pomocí křížového pravidla:
Jestliže platí:![]() , pak b . c = d . a
, pak b . c = d . a
Jestliže
platí: ![]() , pak 3 . 8 = 12 . 2
, pak 3 . 8 = 12 . 2
24 = 24
Příklad:
![]() 3
. ( 2x + 4 ) = 2 . ( 6x – 3 ) Zkouška:
3
. ( 2x + 4 ) = 2 . ( 6x – 3 ) Zkouška:
6x + 12 = 12x – 6 L:
![]()
18 = 6x x = 3
P: ![]() L
= P
L
= P
Vypočítej rovnici a proveď zkoušku:
a) ![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
f)
![]()
g)
![]()
h)
![]()
i)
![]()
j)
![]()
k)
![]()
l)
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2439
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved