| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Definice: Maticí typu (m,n) rozumíme skupinu m n reálných čísel uspořádaných do m řádků a n sloupců (m, n IN). Tato čísla nazýváme prvky matice. Označíme-li aij prvek v i-tém řádku a j-tém sloupci, pak matici typu (m,n) můžeme zapsat ve tvaru
A = zkráceně A=(aij).
zkráceně A=(aij).
Například
B =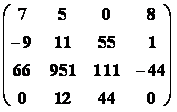
je matice typu (4,4), tj. má 4 řádky a 4 sloupce. Prvek b33 = 111 a prvek b12 = 5 (říkáme prvek v prvním řádku a druhém sloupci má hodnotu 5).
Poznámky
1. Je li m=n říkáme čtvercová matice řádu n .
(předcházející matice byla čtvercová řádu 4)
2. Jsou li všechny prvky nulové říkáme nulová matice. Označíme O. Například nulová matice typu (4,2) zobrazíme
O = 
3. Čtvercová matice řádu n, kde aij = 0 pro i¹j, aij = 1 pro i=j =1,2,¼,n se nazývá jednotková matice řádu n. Označíme E.
E =
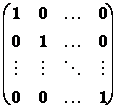
4. Posloupnost a11, a22,a33,,ann se nazývá hlavní diagonála.
(u jednotkové matice řádu n je hlavní diagonála posloupnost n jedniček)
5. Matice typu (m,1) se nazývá sloupcová, např. A = ![]() a matice
typu (1,n) se nazývá řádková,
např. B =
a matice
typu (1,n) se nazývá řádková,
např. B = ![]() . Říká se
také sloupcový nebo řádkový vektor.
. Říká se
také sloupcový nebo řádkový vektor.
6. Transponovaná matice AT k matici A vznikne z A tak, že vyměníme řádky za sloupce a opačně, tj. aTij = aji .
Např. jestliže A =
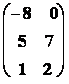 Þ AT =
Þ AT = 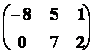
7. Matice A se nazývá symetrická jestliže A = AT, tj. aij = aji . Např.
S = 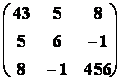
8. Trojúhelníková matice má samé nuly nad nebo pod hlavní diagonálou. Např.
H =  a D =
a D =  jsou
trojúhelníkové matice.
jsou
trojúhelníkové matice.
Definice: Determinant řádu n
je zobrazení množiny všech čtvercových matic řádu n do R. Označíme det A nebo ![]() a definujeme ho indukcí :
a definujeme ho indukcí :
pro n = 1
A = (a11) Þ ![]() = a11
= a11
pro n >
![]() =
= =
= 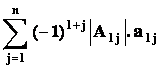 ,
,
kde matice A1j vznikne z A vynecháním prvního řádku a j tého sloupce.
Výpočet determinantu
pro n = 1, A = (a11) Þ ![]() = a11
= a11
n = 2, A
= 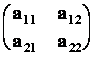 Þ
Þ ![]() =
= 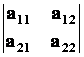 = a 11.a
22 a 12.a 21
= a 11.a
22 a 12.a 21
n = 3, A = 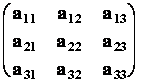 Þ
Þ ![]() =
= 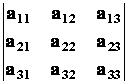 =
=
a 11a 22 a 33 + a 12 a 23 a 31+ a 21a 32 a 13 a 31a 22 a 13 a 21a 12 a 33 a 32 a 23 a 11
(Sarrusovo pravidlo)
Příklady: Vypočtěte determinanty 3. (pomocí Sarrusova pravidla) a 2. řádu.
a) A = 
Řešení : ![]() = 3.0.(-2)+2.(-1).2+1.1.1
= 3.0.(-2)+2.(-1).2+1.1.1
b) H = 
Řešení : det H = ![]() = 6.5.(-4)
= -120 (je vidět, že v
případě troj. matice, det je součin
prvků hlavní diagonály, ostatní součiny jsou nulové)
= 6.5.(-4)
= -120 (je vidět, že v
případě troj. matice, det je součin
prvků hlavní diagonály, ostatní součiny jsou nulové)
c) B = ![]()
Řešení : det B = 5.0 - 1.6 = -6
Poznámka : Přímá analogie Sarrusova pravidla neplatí pro determinanty vyšších řádů. Ty počítáme na základě definice anebo vět uvedených dále.
Definice: Subdeterminantem ![]() matice A příslušným k prvku aik
nazýváme determinant matice, která vznikne z matice A vynecháním i‑tého řádku a k‑tého sloupce. Algebraickým doplňkem k prvku aik
nazýváme výraz
matice A příslušným k prvku aik
nazýváme determinant matice, která vznikne z matice A vynecháním i‑tého řádku a k‑tého sloupce. Algebraickým doplňkem k prvku aik
nazýváme výraz
Dik =
(-1)i+k. ![]()
Věta: Laplaceův rozvoj determinantu
Determinant se rovná součtu součinů prvků libovolného řádku a k ním příslušejících algebraických doplňků :
![]() = a
i1. Di 1 + a i 2. Di 2
+ +a i n. Di n =
= a
i1. Di 1 + a i 2. Di 2
+ +a i n. Di n =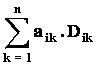
(říkáme, že jsme provedli rozvoj determinantu podle i‑tého řádku)
Poznámka : Analogicky pro sloupce
![]() =
=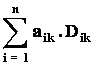 (rozvoj determinantu podle k‑tého
sloupce)
(rozvoj determinantu podle k‑tého
sloupce)
Příklad: Vypočtěte determinant rozvojem :
A = 
Řešení : Počítáme rozvojem podle 2. sloupce (tam je nejvíc nul)
![]() = 0.(-1)1+2.
= 0.(-1)1+2.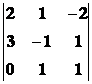 + 0.(-1)2+2.
+ 0.(-1)2+2. + 3.(-1)3+2.
+ 3.(-1)3+2. +
+
+ 1.(-1)4+2.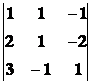 = -1
= -1
Vlastnosti determinantu
Transponováním se determinant nemění, tj. ![]() =
=![]()
Determinant, který má jeden nulový řádek, je roven nule.
Vyměníme‑li v determinantu navzájem dva řádky, determinant změní znaménko.
Determinant, který má dvě stejné řádky, je roven nule.
Vynásobíme‑li jeden řádek čtvercové matice A číslem c, potom
determinant vzniklé matice je roven c.![]() .
.
Hodnota determinantu se nezmění, přičteme‑li k libovolnému řádku násobky ostatních řádků (LK).
Poznámka : Analogicky pro sloupce.
Praktický výpočet determinantů vyšších řádů
Rozvoj determinantu provádíme podle řádku (sloupce), kde je nejvíce nul. Nejsou‑li v žádném řádku (sloupci) nuly, můžeme determinant na základě jeho vlastnosti upravit tak, abychom v určitém řádku (sloupci) získali všechny prvky s výjimkou jednoho nulové.
Příklad: Vypočtěte determinant úpravou :
A = 
Řešení : Nejprve vytkneme 3 (1. sloupec) a 2 (3.)
![]() =
=  = 3.2.
= 3.2.  =
=
a pak odečteme druhý sloupec od třetího a provedeme rozvoj podle 2. řádku, kde je nejvíc nul
= 6. = 6.(-1)
.(-1)2+2.
= 6.(-1)
.(-1)2+2. = (-6).4 = -24
= (-6).4 = -24
Operace s maticemi
Definice: Buďte A, B matice stejného typu (m,n). Klademe
1. Rovnost matic : A = B Û aik = bik i,k
2. Sčítání matic : A + B = (aik + bik)
3. Násobení matice číslem c.A = (c.aik)
Definice: (násobení matic)
Pro matici A typu (m,n) a matici B typu (n,p) klademe
A.B = C
kde výsledná matice C je typu (m,p) a její prvky
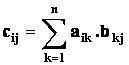
Příklad: Vynásobte matice :
A = 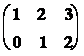 B =
B = 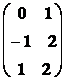
Řešení A.B = 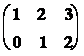
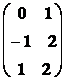 =
=
B.A =
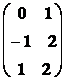
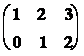 =
=
Hodnost matice
Definice: Maximální počet LN řádků matice A typu (m,n) nazveme hodností této matice. Označujeme hod A nebo h(A).
Hodnost matice se nezmění :
1. Transponováním.
2. Vyměníme‑li navzájem dva řádky.
3. Vynásobíme‑li řádek matice číslem různým od nuly.
4. Přičteme‑li k libovolnému řádku LK ostatních řádků.
5. Vynecháním řádků obsahujících samé nuly.
Poznámka1 : Analogicky pro sloupce.
Poznámka2 : Krokům 1 až 5 říkáme elementární transformace.
Poznámka3 Řekněme, že matice A,B jsou ekvivalentní, lze‑li jednu z nich převést v druhou konečným počtem elementárních transformací. Označíme
A B
Praktický výpočet hodnosti matice
Pomocí elementárních transformací převedeme danou matici na trojúhelníkový tvar. Vynecháme nulové řádky. Počet nenulových řádků této matice je roven její hodnosti.
Příklad: Určete hodnost matice A
A = 
Řešení




Þ h(A) = 3
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2463
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved