| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Mnohoúhelníky
uzavřené lomené čáry spolu s částmi rovin ohraničené těmito lomenými čarami
má vrcholy a strany, lomená čára je hranice mnohoúhelníku (obvod)
úhlopříčky – úsečka spojující
dva nesousední vrcholy jejich počet je dán počtem vrcholů n: ![]() konvexní mnohoúhelník: vždy leží v jedné
z polorovin (opěrná polorovina) určených jednou stranou
konvexní mnohoúhelník: vždy leží v jedné
z polorovin (opěrná polorovina) určených jednou stranou
Konvexní pětiúhelník Nekonvexní mnohoúhelník
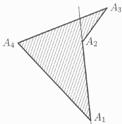
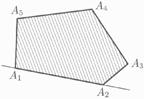
součet vnitřních
úhlů konvexního n-úhelníku se rovná ![]() pravidelný n-úhelník – všechny strany jsou shodné, lze mu
opsat i vepsat kružnici, je-li počet vrcholů sudý existuje ke každému
vrcholu vrchol protější, je-li počet vrcholů lichý existuje ke
každému vrcholu protější strana
pravidelný n-úhelník – všechny strany jsou shodné, lze mu
opsat i vepsat kružnici, je-li počet vrcholů sudý existuje ke každému
vrcholu vrchol protější, je-li počet vrcholů lichý existuje ke
každému vrcholu protější strana
Konstrukce mnohoúhelníků (![]() ;
; ![]() , kde
, kde ![]() )
)
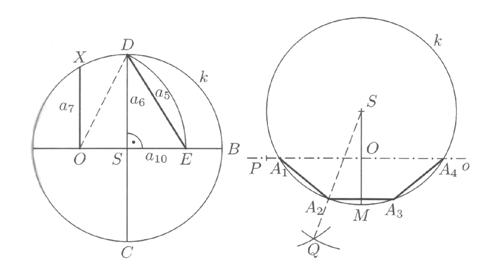
Osmiúhelník – osa strany čtverce, trojúhelník – osy stran šestiúhelníku
Čtyřúhelníky
n-úhelníky se 4 vrcholy
dělíme je:
o různoběžníky – žádné dvě strany nejsou rovnoběžné
o lichoběžníky – dvě strany jsou rovnoběžné a dvě ne, rovnoběžné strany = základy různoběžné – ramena
základny nejsou shodné, ramena mohou být (pokud jsou jde o rovnoramenný lichoběžník)
je-li jedno rameno kolmé k jedné základně, pak je kolmé i k druhé základné, jedná se o pravoúhlý lichoběžník
součet vnitřních úhlů přilehlých ramenu je přímý úhel
střední příčka je úsečka spojující středy jeho ramen, je rovnoběžná se základnami a její délka je rovna aritmetickému průměru obou základen
o rovnoběžník – každé dvě strany jsou rovnoběžné
podle vlastnosti úhlů:
pravoúhlé (obdélník)
kosoúhlé (kosodélník)
podle stran
rovnostranné (čtverec, kosočtverec)
různostranné (obdélník, kosodélník)
základní vlastnosti rovnoběžníku
protější strany jsou shodné
protější úhly jsou shodné
úhlopříčky se navzájem půlí, společný bod je střed rovnoběžníku
tětivový rovnoběžník – lze mu opsat kružnici (součet vnitřních úhlů je úhel přímý)
tečnový rovnoběžník – lze mu vepsat kružnici (součty délek dvojic protějších stran jsou si rovny)
středový rovnoběžník – lze mu opsat i vepsat kružnici
deltoid – úhlopříčky jsou si navzájem kolmé a jedna (hlavní) prochází středem druhé (vedlejší), je to tečnový rovnoběžník
Kružnice, kruh
Kružnice – množina všech bodů, které mají od určitého bodu S stejnou vzdálenost r.
Kruh – množina všech bodů, které mají od určitého bodu S vzdálenost rovnu nebo menší než r.
bod S je střed kružnice (kruhu) a r je poloměr
u kruhu určujeme jeho hranici – kružnice, vnitřek (vnitřní oblast), vnějšek (vnější oblast)
tětiva – úsečka, která spojuje dva různé body kružnice, tětiva, která prochází středem je průměr kružnice
různé body A,B dělí kružnici na dva kružnicové oblouky (oblouky kružnice) a body A,B jsou krajními body obou oblouků a oblouk značíme , množina všech vnitřních bodů oblouku je otevřený oblouk AB, je-li AB průměr jsou oba oblouky půlkružnice
dva poloměry rozdělí kruh na dvě kruhové výseče a tětiva je rozdělí na dvě kruhové úseče, pokud je tětiva průměr tak na dva půlkruhy
Vzájemná polohy přímky a kružnice
sečna – dva společné body
tečna – je společný bod – bod dotyku
vnější přímka – žádný společný bod
Platí:
pata kolmice vedené ze středu na sečnu je střed tětivy
tečna kružnice je kolmice na poloměr, který spojuje bod dotyku a střed
délka tečny – vzdálenost bodu dotyku a bodu, ze kterého tečna vychází
Vzájemná poloha dvou kružnic
soustředné – společný střed,
nemají společný bod, nebo je mají všechny společné, pak jsou totožné,
pokud je poloměr jedné menší vytvářejí tzv. mezikruží, ![]() je šířka
mezikružínesoustředné
je šířka
mezikružínesoustředné
o kružnice leží vně druhé
o kružnice mají vnější dotyk
o kružnice mají vnitřní dotyk
o kružnice leží uvnitř druhé
Úhly v kružnici
středový úhel – vrchol je střed kružnice, vytýká oblouk
obvodový úhel – vrchol leží na kružnici a ramena procházejí krajními body oblouku
velikost středového úhlu je rovna dvojnásobku velikosti obvodového úhlu stejného oblouku
Thaletova věta:
Všechny úhly nad průměrem kružnice jsou pravé.
úsekový úhel – úhel, který svírají rameno AB, kde A,B jsou krajní body oblouku a rameno AX, kde X je vnější bod kružnice, který leží na tečně, která má bod dotyku v bodě A, je stejně velký jako obvodový úhel příslušného oblouku
Obvody a obsahy geometrických obrazců
geometrický obrazec – geometrický útvar ohraničený uzavřenou čárou , která je částí obrazce
obvod – délka hranice obrazce
obsah – kladné číslo přiřazené obrazci
Euklidova věta o výšce
![]() , V každém pravoúhlém trojúhelníku je druhá mocnina
výška rovná součinu délek úseků přepony.Euklidova věta o odvěsně
, V každém pravoúhlém trojúhelníku je druhá mocnina
výška rovná součinu délek úseků přepony.Euklidova věta o odvěsně
![]() , V každém pravoúhlém trojúhelníku je druhá mocnina
délky odvěsny rovna součinu přepony a přilehlého úseku
přepony.Pythagorova věta
, V každém pravoúhlém trojúhelníku je druhá mocnina
délky odvěsny rovna součinu přepony a přilehlého úseku
přepony.Pythagorova věta
Obsah čtverce sestrojeného nad
přeponou pravoúhlého trojúhelníku se rovná součtu čtverců
sestrojených nad oběma odvěsnami. ![]()
Mocnost bodu ke kružnici
vedeme-li bodem M přímku,
která je sečnou kružnice pak mocnost
m bodu ke kružnici je:![]() pokud takto vedeme více sečen mocnost se nemění
pokud takto vedeme více sečen mocnost se nemění
pokud ![]() pak bod M je vně
kružnice, pokud
pak bod M je vně
kružnice, pokud ![]() pak leží na kružnici a
pokud
pak leží na kružnici a
pokud ![]() pak leží uvnitř
kružnicevedeme-li tečnu a sečnu bodem ke kružnici platí
pak leží uvnitř
kružnicevedeme-li tečnu a sečnu bodem ke kružnici platí ![]() je-li v vzdálenost bodu od středu kružnice pro
mocnost platí:
je-li v vzdálenost bodu od středu kružnice pro
mocnost platí: ![]()
|
Trojúhelník |
|
Heronův vzorec:
|
|
|
Obdélník |
|
|
|
|
Čtverec |
|
|
|
|
Kosodélník |
|
|
|
|
Kosočtverec |
|
|
|
|
Lichoběžník |
|
|
|
|
Kruh |
|
|
|
|
Mezikruží |
|
|
|
|
Pravidelný n-úhelník |
|
|
|
|
oblouk |
|
|
|
|
Kruhová výseč |
|
|
|
|
Kruhová úseč |
|
|
|
|
Elipsa |
|
|
|
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2403
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved
Distribuie URL
Adauga cod HTML in site