| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Definice: Vektorový prostor nad R
nazýváme neprázdnou množinu V ( V ¹ ![]() , prvky
nazýváme vektory ), na které jsou definovány operace sčítání a násobení :
, prvky
nazýváme vektory ), na které jsou definovány operace sčítání a násobení :
(+) ![]() (součet dvou vektorů je také
vektor)
(součet dvou vektorů je také
vektor)
![]() ( násobek
vektoru je také vektor)
( násobek
vektoru je také vektor)
Přitom tyto
operace splňují ![]() následující podmínky :
následující podmínky :
![]() komutativnost
komutativnost
![]() asociativnost
asociativnost
![]() existence nulového vektoru
existence nulového vektoru
![]() existence opačného vektoru
existence opačného vektoru
![]() distributivnost
distributivnost
![]() distributivnost
distributivnost
![]() asociativnost
asociativnost
![]() existence
jednotkového prvku
existence
jednotkového prvku
Příklad: Nechť L je množina přirozených čísel, na které definujeme součet přirozených čísel a reálný násobek přirozeného čísla „obvyklým způsobem“. Máme rozhodnout, zda L je vektorový prostor.
Řešení : Aby L byl vektorový prostor, muselo by podle definice platit:
a) Pro všechny vektory ![]() je jejich
součet
je jejich
součet ![]() opět vektor z L, tj. množina je uzavřena vůči sčítání.
opět vektor z L, tj. množina je uzavřena vůči sčítání.
b) Pro každé cIR a ![]() je
je ![]() opět vektor z L, tj. množina je uzavřena vůči násobení vektoru reálným číslem.
opět vektor z L, tj. množina je uzavřena vůči násobení vektoru reálným číslem.
c) V množině L platí podmínky 1. až 8.
Protože existuje cIR a pIN takové, že c.pÏN (například pro c = -1, p = 1), není N uzavřená vůči násobení reálným číslem. Množina L není vektorový prostor.
Příklady vektorových prostorů
1. Množina komplexních čísel, na které je obvyklým způsobem definováno sčítání a násobení komplexních čísel číslem reálným.
2. Množina všech spojitých funkcí jedné reálné proměnné na intervalu ![]() .
.
3. Množina všech uspořádaných n-tic reálných čísel
![]() kde
operace jsou definovány vztahy :
kde
operace jsou definovány vztahy :
(+) : ![]()
: ![]()
(aritmetický n‑rozměrný vektorový prostor)
4. Množina všech orientovaných úseček v rovině s počátečním bodem [0,0].
(geometrický model vektorového prostoru)
Definice: Buď V vektorový prostor nad R, ![]() .
Existují-li taková čísla
.
Existují-li taková čísla ![]() , že
, že
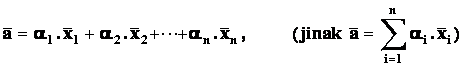
pak říkáme,
že vektor ![]() je lineární
kombinací (LK) ostatních vektorů.
je lineární
kombinací (LK) ostatních vektorů.
Definice: Buď V vektorový prostor nad R, vektory ![]() nazveme lineárně
závislé (LZ) jestliže platí
nazveme lineárně
závislé (LZ) jestliže platí
(![]() ) Ù (alespoň jedno z čísel
) Ù (alespoň jedno z čísel ![]() )
)
Platí-li
rovnost pouze pro ![]() potom řekneme, že vektory
potom řekneme, že vektory ![]() jsou lineárně
nezávislé (LN).
jsou lineárně
nezávislé (LN).
Poznámka : Když ![]() pak
pak 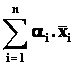 nazýváme
triviální LK.
nazýváme
triviální LK.
Důsledek : ![]() jsou LZ
jsou LZ![]() alespoň
jedna jejich netriviální lineární kombinace rovná
alespoň
jedna jejich netriviální lineární kombinace rovná ![]() .
.
Vlastnosti LN vektorů
1. Lineární nezávislost nezáleží na pořadí vektorů.
2. Pokud skupina vektorů
obsahuje ![]() Þ vektory jsou LZ.
Þ vektory jsou LZ.
3. Jsou-li vektory ![]() lineárně nezávislé, pak vynásobíme-li
libovolný z vektorů číslem c¹0,
dostaneme opět LN vektory.
lineárně nezávislé, pak vynásobíme-li
libovolný z vektorů číslem c¹0,
dostaneme opět LN vektory.
4. Jsou-li vektory ![]() lineárně nezávislé, pak přičteme-li k
libovolnému vektoru LK ostatních, dostaneme opět LN vektory.
lineárně nezávislé, pak přičteme-li k
libovolnému vektoru LK ostatních, dostaneme opět LN vektory.
Věta: Vektory ![]() jsou LZ Û alespoň
jeden z nich lze vyjádřit jako LK
ostatních.
jsou LZ Û alespoň
jeden z nich lze vyjádřit jako LK
ostatních.
Příklad: Jsou
dány vektory ![]() =(1,-1,1),
=(1,-1,1), ![]() =(2,3,0),
=(2,3,0), ![]() =(-1,-4,1),
z aritmetického vektorového prostoru R3. Posoudíme, zda jsou LZ či
LN.
=(-1,-4,1),
z aritmetického vektorového prostoru R3. Posoudíme, zda jsou LZ či
LN.
Řešení : Hledáme reálná čísla a b c , vyhovující rovnici :
![]() = a
= a![]() b
b![]() c
c![]()
Po dosazení aritmetických vektorů ![]() ,
, ![]() ,
, ![]() a nulového vektoru
a nulového vektoru ![]() =(0,0,0) a
provedení operací na pravé straně dostaneme
=(0,0,0) a
provedení operací na pravé straně dostaneme
(0,0,0) = ( a b c a b c a c
Odtud máme soustavu tří lineárních rovnic pro tři neznámé a b c
a b c
-a b c
a c
Tato soustava má vždy řešení a b c = 0. Musíme rozhodnout, jestli je toto řešení jediné, nebo existuje další řešení, ve kterém je alespoň jedna neznámá různá od nuly. Protože soustavě například vyhovuje a b c = ‑1, jsou vektory lineárně závislé.
Poznámka: Množina všech lineárních kombinací vektorů ![]() V je
vektorový prostor. Skupinu vektorů
V je
vektorový prostor. Skupinu vektorů ![]() nazýváme určující
skupinou tohoto vektorového prostoru.
nazýváme určující
skupinou tohoto vektorového prostoru.
Definice: Báze vektorového prostoru je lineárně nezávislá určující skupina vektorů tohoto prostoru. Počet vektorů báze se nazývá dimenze vektorového prostoru.
Příklad: Jednotkové vektory v aritmetickém vektorovém prostoru R3 ,
![]() = (1,0,0),
= (1,0,0), ![]() = (0,1,0),
= (0,1,0),
![]() =(0,0,1),
=(0,0,1),
jsou příkladem báze
tohoto prostoru. Snadno se totiž přesvědčíme, že pro každé ![]() I R3 platí
I R3 platí
![]() (
(![]() ,
,![]() ,
,![]() je určující skupina)
je určující skupina)
a rovnice
![]() = a
= a![]() b
b![]() c
c![]()
má jediné řešení a b c = 0. (![]() ,
,![]() ,
,![]() jsou lineárně nezávislé)
jsou lineárně nezávislé)
Podprostory
Definice: Podprostorem vektorového prostoru V nazveme neprázdnou podmnožinu W z V, uzavřenou vůči sčítání a vůči násobení vektoru reálným číslem, tj.
![]() .
.
Definice: Jestliže ![]() V (vektorový
prostor nad R). Množina všech LK těchto vektorů se nazývá lineární obal vektorů
V (vektorový
prostor nad R). Množina všech LK těchto vektorů se nazývá lineární obal vektorů ![]() . Značíme <
. Značíme <![]() >
>
Dá se dokázat, že je to podprostor prostoru V.
Příklad: Rozhodněte, zda množina L je podprostorem vektorového prostoru R4, jestliže
L =
Řešení : L je podprostor jestliže je sám vektorový prostor. Mějme v,wIL tj.
v = (v1,v2,v3,v4)I R4, v1+v2+v3+v4 = 0 a
w = (w1,w2,w3,w4)I R4, w1+w2+w3+w4 = 0
Pak
v + w = (v1+ w1,v2+ w2,v3+ w3,v4+ w4)I R4 a součet složek
v1+ w1+v2+ w2+v3+ w3+v4+ w4 = (v1+v2+v3+v4 )+( w1+w2+w3+w4 ) = 0.
Čili součet (v+w)IL , tj. množina je uzavřena vůči sčítání. Navíc
c.v = (c.v1,c.v2,c.v3,c.v4)I R4 a
c.v1+c.v2+c.v3+c.v4 = c. (v1+v2+v3+v4 ) = c.0 = 0
Čili součin c.v IL , tj. množina je uzavřena vůči násobení vektoru reálným číslem.
Protože je zřejmé, že budou splněné i podmínky, pak můžeme říci, že L je podprostorem vektorového prostoru R4.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1095
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved