| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Zákon rozdělení poruch
Nejsnadnější zjištění zkouškou z velkého počtu systémů
Záznamy
![]() Doby poruch jednotlivých systémů
Doby poruch jednotlivých systémů
Počty poruch systémů v krátkém časovém intervalu (vzhledem k trvání testu)
následuje statistické zpracování
Prostá tabelace poruchovosti (nepraktické, nepoužívá se)
Porovnání průběhu poruchovosti s některým standardním rozdělením a určení parametrů rozdělení
Nalezené (zvolené) rozdělení umožní dopočítat všechny potřebné charakteristiky (včetně dalších stavů jako např.: čekání na opravu, bezporuchovost, porucha zálohy aj.)
Rozdělení spojité náhodné proměnné
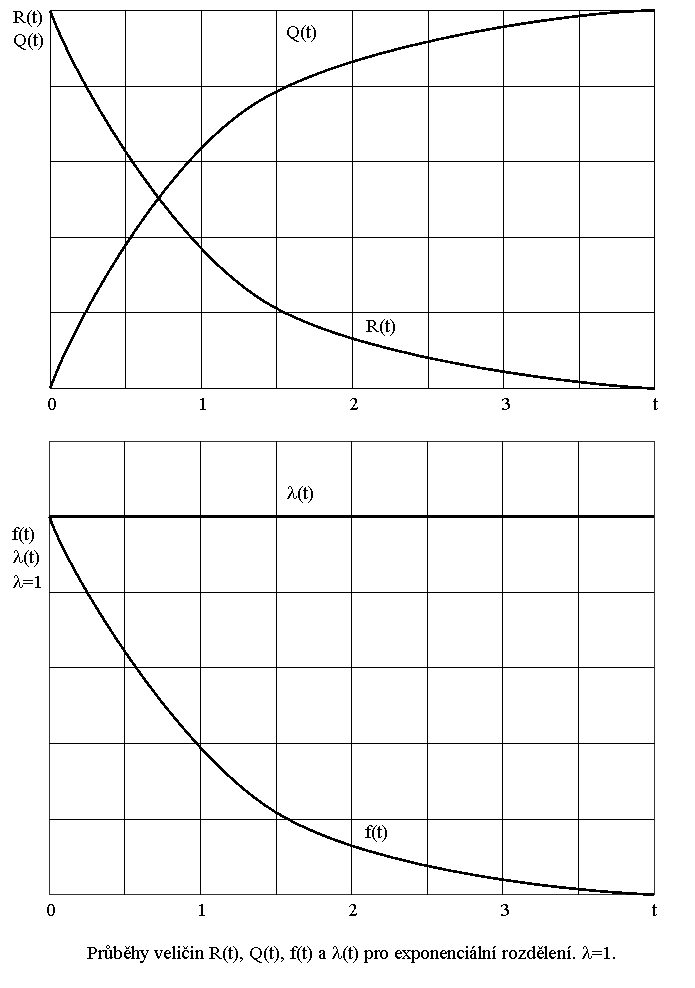
Exponenciální rozdělení: jeden parametr l>0 pro t![]() 0
0
výhodné: jednoduché analytické výrazy
při nedostatku údajů o chování systému se snadněji určí
R(t)=exp(-l.t)
Q(t)=1-exp(-l.t)
f(t)= l.exp(-l.t)
l(t)= l
TS=1/l
D=1/l
Pozn. (1) Nejčastěji užívané !
Střední doba bezporuchového
provozu 1/l ![]() rozložení je určeno střední hodnotou.
rozložení je určeno střední hodnotou.
Vhodná aproximace chování systémů v období normálního provozu !
Neodpovídá chování v období počátečního provozu a období dožívání systému !
Některé typy systémů s proměnnou intenzitou poruch (l) nejsou pro popis exp. rozdělením vhodné.
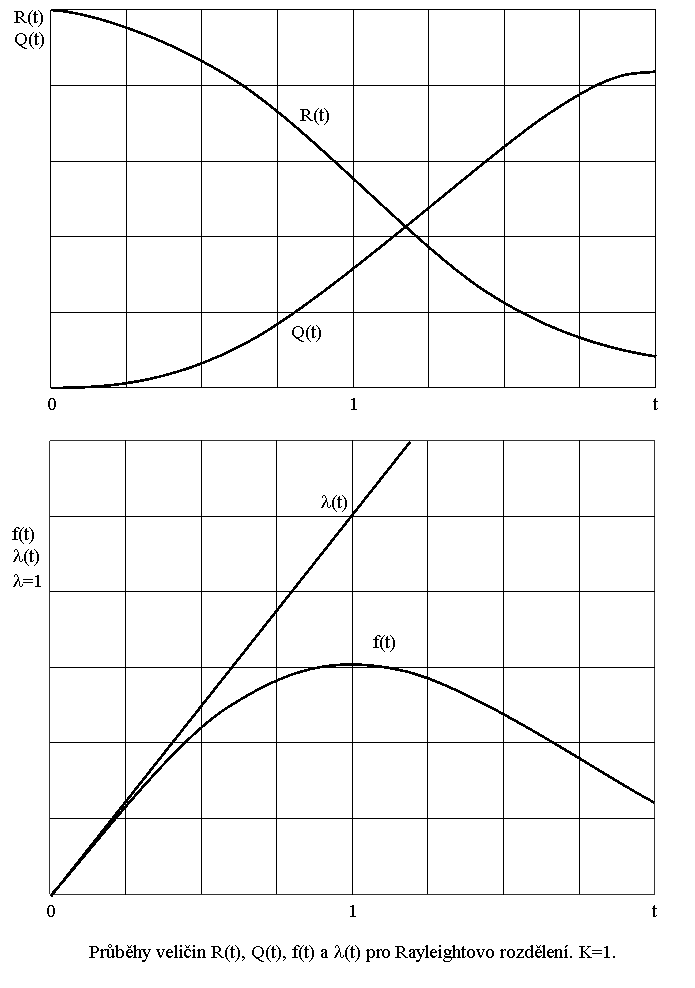
Rayleightovo rozdělení je určeno jedním parametrem, intenzita poruch roste lineárně s časem
parametr
rozdělení: k![]() 0
pro t
0
pro t![]() 0
0
R(t)=exp(![]() )
)
Q(t)=1- exp(![]() )
)
f(t)=k.t. exp(![]() )
)
l(t)=k.t
TS=![]()
D=(2-![]() )/k=
)/k=![]()
Wiebullovo rozdělení: původně 3 parametry, pro účely spolehlivosti se parametr posunutí v čase nuluje.
parametry rozdělení: m>0
t0>0
pro t![]()
R(t)=exp(![]() )
)
Q(t)=1- exp(![]() )
)
f(t)=. exp(![]() )
)
l(t)=![]()
TS=t01/mG(![]() )
)
D= t02/m G(![]() )-G (
)-G (![]() )]
)]
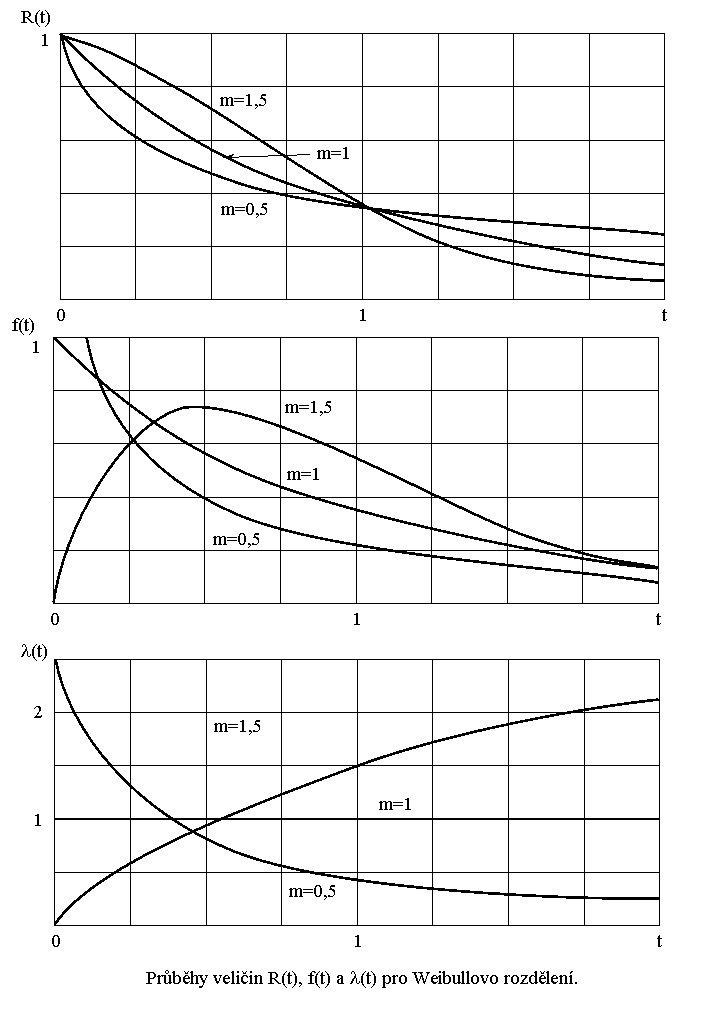
Wiebullovo rozdělení zahrnuje exponenciální rozdělení a Rayleightovo rozdělení jako spec. případy.
pro
m=1 ![]() exp. rozdělení
exp. rozdělení
pro
m=2 ![]() Rayleightovo rozdělení
Rayleightovo rozdělení
Charakteristiky Wiebullova rozdělení pro m<1 aproximují období počátečního provozu systému
Po exponenciálním rozdělení je Wiebullovo rozdělení 2. Nejpoužívanější
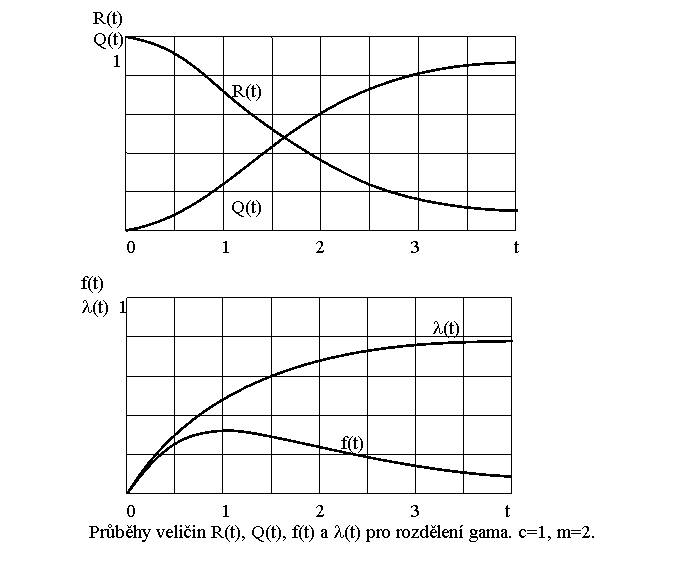
 Rozdělení gama: dva parametry m>0, c>
Rozdělení gama: dva parametry m>0, c>
čas
t![]() 0
0
uplatnění při popisu soustav se zálohováním
f(t)=![]()
TS=m.c
D=m.c2
je-li m celé číslo, je ![]() tedy:
tedy:
f(t)=![]()
kde: m…změna tvaru funkce f(t)
c…změna měřítka na osách
rozdělení gama je pro m=1 exponenciálním rozdělením s l=1/c
hodnoty ![]() a F(t) jsou tabelovány
a F(t) jsou tabelovány
 Normální rozdělení: dva parametry m, s > 0
Normální rozdělení: dva parametry m, s > 0
čas t![]() 0
0
f(t)=
kde 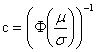
![]() …distr.
funkce normovaného rozdělení, tj.: mn
…distr.
funkce normovaného rozdělení, tj.: mn
sn
tedy ![]() :
:
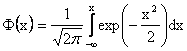
hustota pravděp. normálního rozdělení:
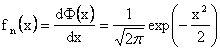
POZOR,
pro účely spolehlivosti se pracuje s t![]() 0
tj. pravděp. je =0,
0
tj. pravděp. je =0, ![]() t<0
tj. charakteristiky bezporuchovosti pro „useknuté“ rozdělení: t>0
t<0
tj. charakteristiky bezporuchovosti pro „useknuté“ rozdělení: t>0
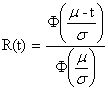
![]()
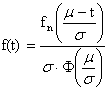
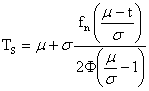
pro m > s je TS liší minimálně od m
„useknuté“ normované rozložení (viz obr.) je vhodné pro aproximaci charakteristik bezporuchovosti v období dožívání výrobku
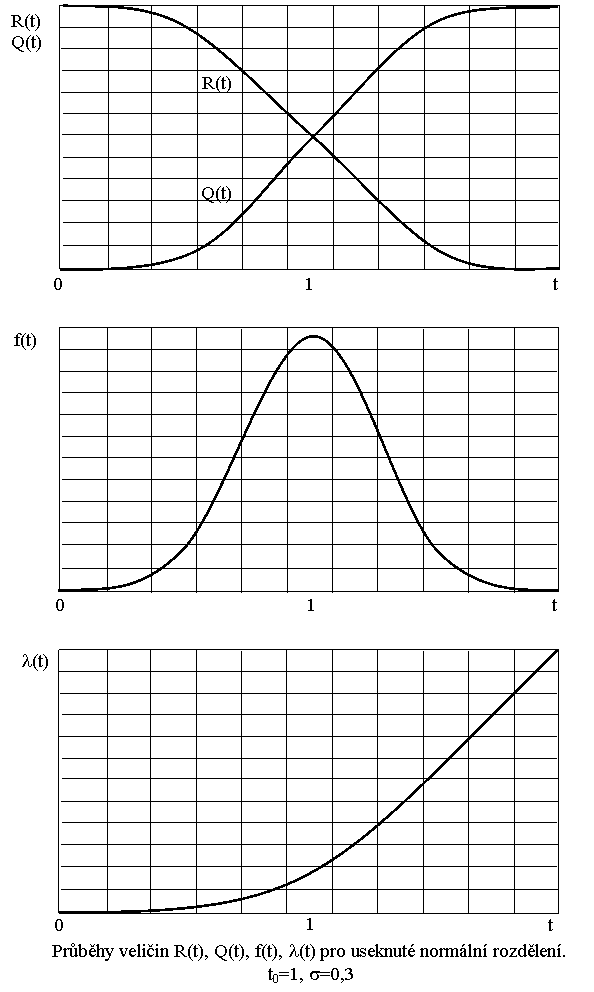
Logaritmické – normální rozdělení
logaritmus náhodné proměnné t má normální rozdělení, tedy:
hustota pravděp.
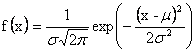 kde:
kde: ![]()
dosazením:
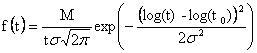
kde: konstanta M![]() 0,4343
je pro převod ln
0,4343
je pro převod ln![]() log
log
Střední doba rozdělení:
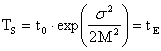
logaritmováním a dosazováním za M:
![]()
Rozptyl:
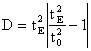
pro malé velikosti s < 0.1 je podobné normální rozdělení, použití v době obnovy soustavy
předchozí jednoduchá rozdělení
neaproximují dostatečně přesně soustavu po celou dobu jejího života ![]() kombinace jednoduchých rozdělení
kombinace jednoduchých rozdělení
aproximace bezporuchovosti v obdobích počátečního provozu + normálního provozu
R(t)=c1exp(-l .t) + c2exp(-l .t)
f(t)= l c1exp(-l .t) + l c2exp(-l .t)
musí platit: 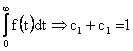
tedy: ![]()
počáteční hodnota: l(0) l c1+ l c2
![]()
je-li (typicky) l < l při dostatečně velkém t je exp(-l t) blíže k 0 než
exp(-l t)![]() >>1
přejde rozdělení v exponenciální rozdělení s l(t)
>>1
přejde rozdělení v exponenciální rozdělení s l(t)![]() l1(t)
l1(t)
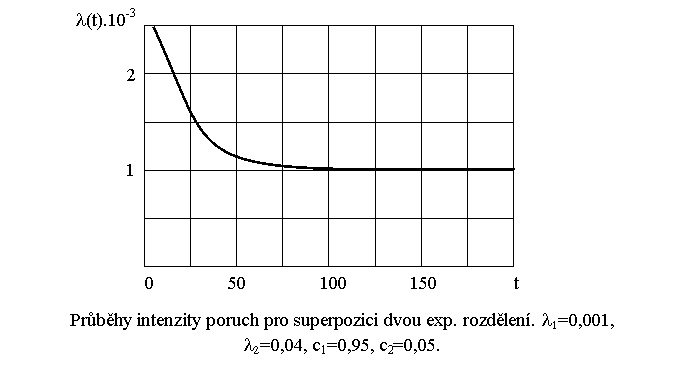
vhodné pro aproximaci poruchovosti v obdobích normálního provozu + dožívání výrobku
výsledná intenzita poruch: l(t)= l1(t)+ l2(t)
potom pravděp. bezporuchového provozu
![]()

![]()
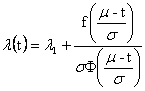
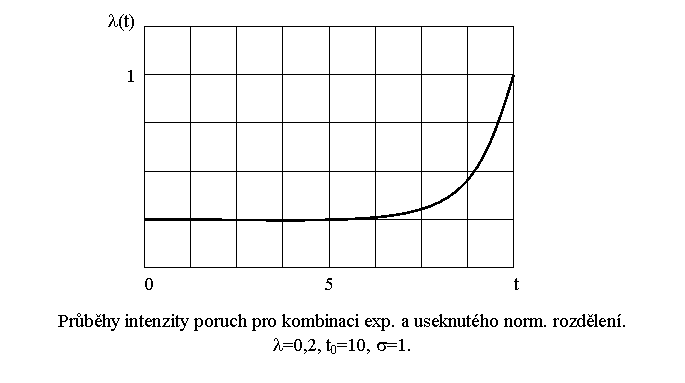
všechna tři období provozu lze
aproximovat dobře Wienbullovým rozdělením nebo superpozicí dvou exp. rozdělení
vždy v kombinaci s useknutým normálním rozdělením (t![]() 0)
0)
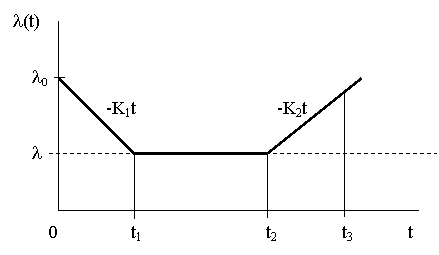 tzv. „vanová křivka“
tzv. „vanová křivka“
úseky konstantní intenzita poruch ![]() exp. rozdělení
exp. rozdělení
rostoucí
intenzita poruch ![]() Reiteighovo rozdělení
Reiteighovo rozdělení
klesající
intenzita poruch ![]() viz dále
viz dále
Situace s klesající intenzitou poruch
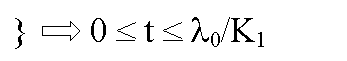 Pro t=0 počáteční hodnota l jež lineárně klesá k 0
Pro t=0 počáteční hodnota l jež lineárně klesá k 0
tedy l(t)=l -K1t
l(t) l(t)![]() 0
0
![]() t
t![]() 0
0
 rozdělení
je dvouparametrové
rozdělení
je dvouparametrové
l ,K1
nicméně
nesplňuje podmínku, že pro
t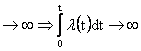
řešení zavedení konstantní složky l(t)=konst
nebo l(t)=fce(t) rostoucí s t
pravděp. bezporuchového provozu se stanoví integrací l(t) dle t
rozdělení oboru integrace na 3 intervaly (viz předchozí obr.) dosazením do vztahu
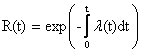
tedy pro po částech lineární rozložení platí (viz obr.)
![]() t; 0
t; 0![]() t
t![]() t1: l(t)=l -K1t
t1: l(t)=l -K1t
R(t)=exp(-l t+0,5K1t2)=R1t
mez
intervalu: ![]()
![]() t; t1
t; t1![]() t
t![]() t2: l(t)=l
t2: l(t)=l
R(t)=exp(-l t+0,5K1t12-l(t-t1))
dosazením ze rovnice:
R(t)=R1(t1)exp(-l(t-t1))=R2(t)
![]() t; t2
t; t2![]() t
t![]() t3: l(t)=l+K2(t)
t3: l(t)=l+K2(t)
R(t)= R2(t2)exp(-l(t-t2)-0,5K2(t-t2)2)
![]()
*
Pozn. 1) Součiny výrazů výše ozn. * reprezentují
současný výskyt jevů
(pravděp.), že:
„porucha nenastala do začátku intervalu“ x
x „pravděp. bezporuchového provozu
uvnitř intervalu“
2) mez intervalu t3 je možno
posouvat až do ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 886
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved