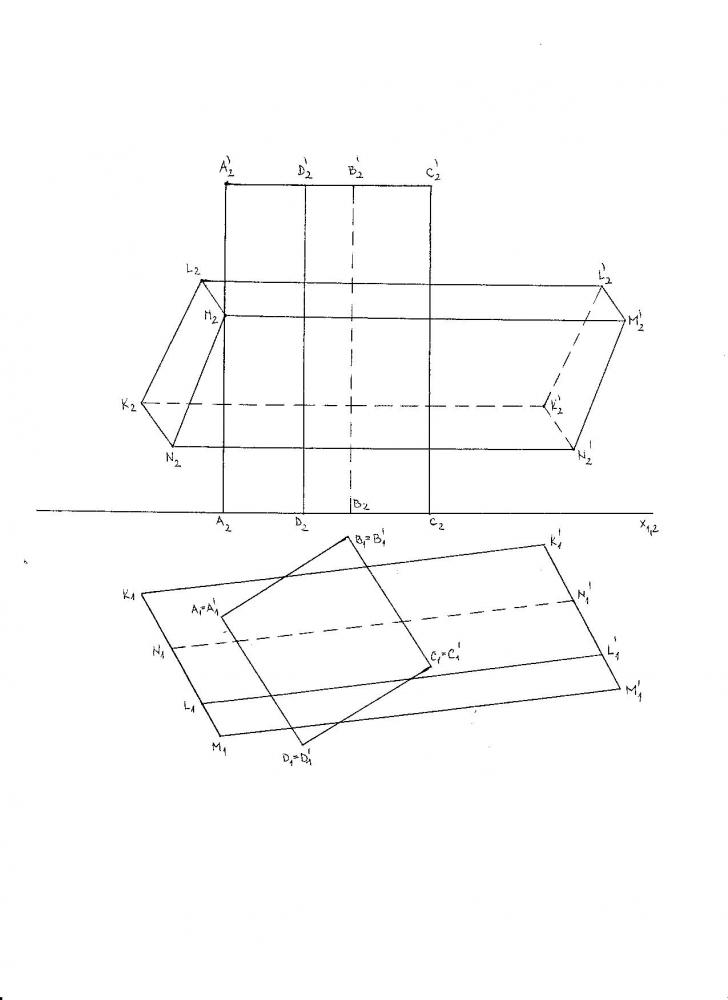
Průnik dvou hranolů
Průnik dvou hranolů Kolmý čtyřboký hranol s podstavou v půdorysně a čtyřboký hranol s podstavou v rovině kolmé k půdorysně. Jedná se o úplný průnikCiteste tot ... 150 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
DIFERENCE A DIFERENČNÍ ROVNICE (DR)
DIFERENCE A DIFERENČNÍ ROVNICE (DR) §1 Funkce a posloupnosti Termínem funkce budeme nadále rozumět reálnou funkci jedné reálné proměnné definovanou na intervalu J. Termínem posloupnost budeme rozumět reálnou posloupnost definovanou na množiněCiteste tot ... 1248 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
Pravděpodobnost
Pravděpodobnost P(A Č B) = P(A) + P(B) - P(A Ç B) P(A Ç B) = P(A / B) . P(B) = P(B/A) . P(A) Binomické rozdělení , k = 0, 1, …, n E(X) = np D(X) = np(Citeste tot ... 1438 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
MATICE A DETERMINANTY
matice a determinanty Definice: Maticí typu (m,n) rozumíme skupinu m´n reálných čísel uspořádaných do m řádků a n sloupců (m, n IN). Tato čísla nazýváme prvky matice. Označíme-li aij prvek v i-tém řádku a j-tém sloupci, paCiteste tot ... 730 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
Zákon rozdělení poruch
Zákon rozdělení poruch · Nejsnadnější zjištění zkouškou z velkého počtu systémů · Záznamy: 1. Doby poruch jednotliCiteste tot ... 538 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
GRUPA
GRUPA Numerički nizovi Distribucija frekvencija &nCiteste tot ... 1508 cuvinte
Dimensiune medie
+ cu poze |
 |
 |
LIMITA A SPOJITOST FUNKCE
limita a spojitost funkce Definice: Okolím reálného čísla a nazýváme otevřený interval , kde d je libovolné kladné číslo („delta okolí“). Je to tedy množina reálných čísel x, které vyhovují nerovnostCiteste tot ... 796 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
Kombinatorika a pravděpodobnost
Kombinatorika a pravděpodobnost 8.1. Kombinatorika Přehled vzorců: Permutace (bez opakování) – uspořádané n–tice z daných n prvků (skupiny, které obsahují všechny dané prvky a liší se pouze jejich poCiteste tot ... 1791 cuvinte
Dimensiune medie
+ cu poze |
 |
 |
Průsečíky přímek s tělesy
Průsečíky přímek s tělesy Postup konstrukce: 1. Danou přímkou proložíme vhodnou rovinu 2. Sestrojíme řez tělesa touto rovinou 3Citeste tot ... 221 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
Cvičné příklady
Cvičné příklady Napište algoritmus, pomocí něhož postupně uložíte 3 hodnoty do proměnných a1, a2, a3 a určíte počet proměnných, jejichž hodnota je rovna 1. Počet vypište.Citeste tot ... 1947 cuvinte
Dimensiune medie
+ cu poze |
 |
 |
KNIHA KÓDŮ A ŠIFER
Kniha kódů a šifer Simon Singh Utajování od starého Egypta po kvantovou kryptografii Vydala roku 2003 nakladatelství Dokořán a Argo „Touha odhalovat tajemství je hluboce zakořeněna v lidské přirozenostiCiteste tot ... 94530 cuvinte
Dimensiune mare
+ cu imagini |
 |
 |
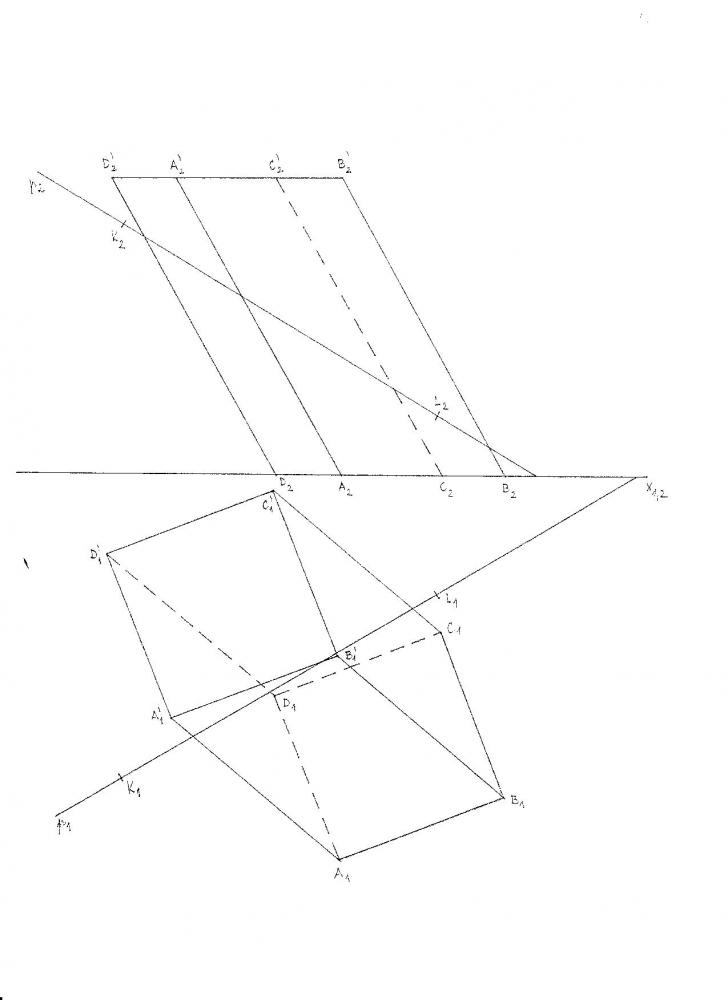
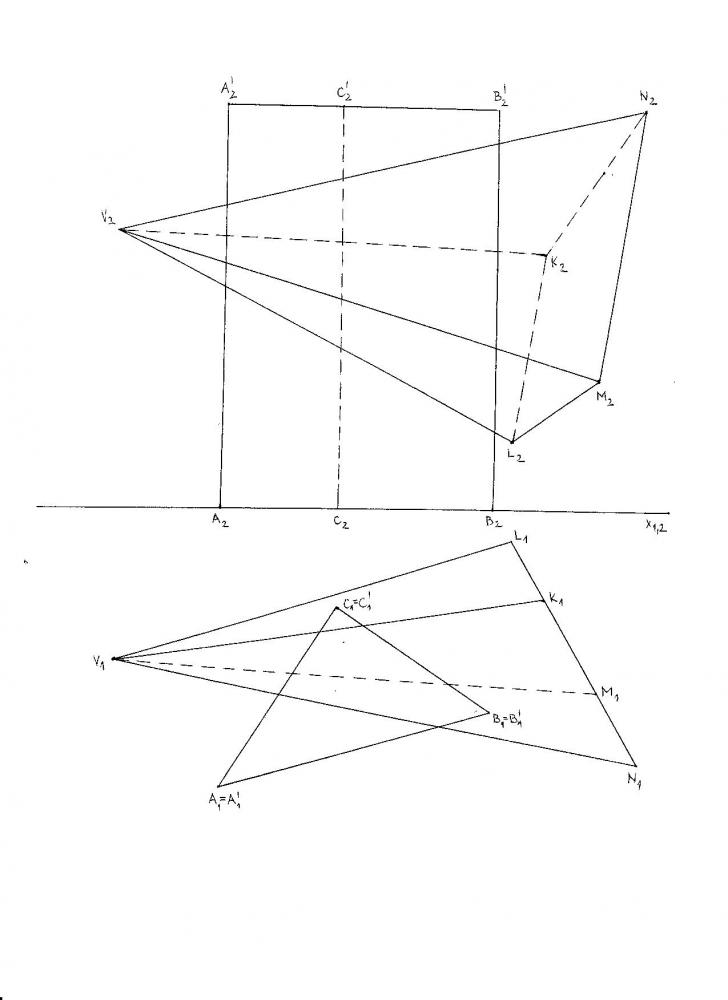
Průnik hranolu s jehlanem
Průnik hranolu s jehlanem Kolmý trojboký hranol s podstavou v půdorysně a čtyřboký jehlan s podstavou v rovině kolmé k půdorysně. Jedná se o částečný pCiteste tot ... 143 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
Množiny, kružnice
Množiny, kružnice - množinou rozumíme soubor prvků, které mají jistou společnou vlastnost - označení množin: A,B,C,… - &nCiteste tot ... 184 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
KOMBINATORIKA
KOMBINATORIKA Přehled vzorců: Permutace (bez opakování) – uspořádané n-tice z daných prvků (skupiny, které obsahují všechny dané prvky a liší se pouze jejich pořadím). Počet permutací z Citeste tot ... 195 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
Mocniny, Elipsa
Mocniny, Elipsa ( Maturitní otázka č.2 ) a n - mocnina a - základ mocniny n - mocnitel ( exponent ) Pravidla pro počítání s mocninami Částečné odmocňování:Citeste tot ... 194 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
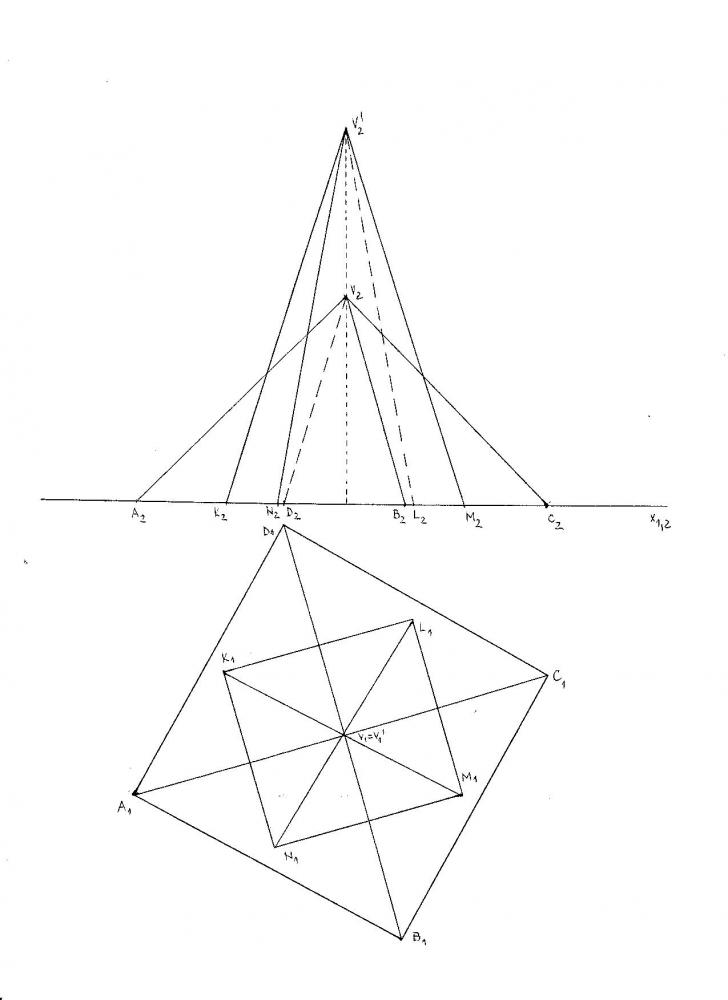
Průnik dvou jehlanů
Průnik dvou jehlanů oba jehlany stojí na půdorysně, mají společnou osu. Hranami AV a CV „nižšího“ jehlanu proložíme rovinu kolmou k půdorysně. Vyznačíme průsečíky s&Citeste tot ... 119 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
VEKTOROVÉ PROSTORY
Vektorové prostory Definice: Vektorový prostor nad R nazýváme neprázdnou množinu V ( V ¹ , prvky nazýváme vektory ), na které jsou definovány operace sčítání a násobení : (+) (součet dvou vektorůCiteste tot ... 651 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
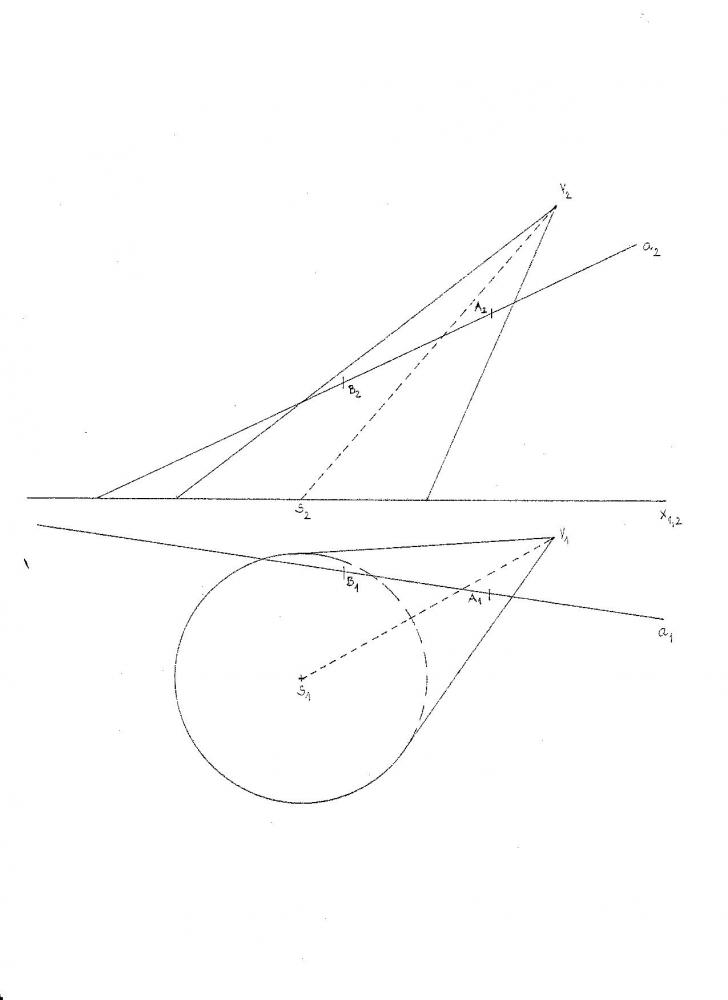
Průsečíky přímky s kuželem
Průsečíky přímky s kuželem Nejlépe je volit rovinu řezu tak, aby procházela vrcholem daného kužele, řezem kužele potom bude trojúhelník, který snadno sestrojíme – najdeme průsečíky stopy s podstavou a spojCiteste tot ... 111 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
INVERZNÍ MATICE
Inverzní matice Definice: Pokud =0, potom čtvercovou matici A nazveme singulární. V opačném případě nazveme regulární. Definice: Matici X nazveme maticí inverzní k regulární matici A, jestliže platí : Citeste tot ... 73 cuvinte
Dimensiune mica
+ cu imagini |
 |
 |
ANALYTICKÁ GEOMETRIE
Analytická geometrie §2.1 úvod Příklad1: GEM řešte homogenní SLR : Řešení : =~Þh(A) = h() = 2 < n Þ soustava má nekonečně mnoho řešení, která jsou závislá na volbě (n-h)Citeste tot ... 2225 cuvinte
Dimensiune medie
+ cu poze |
 |
 |
Alte pagini