The International Cost of Capital and Risk Calculator (ICCRC)

The International Cost of Capital and Risk Calculator (ICCRC)

Introduction

The goal of this paper is to provide the economic background for the International Cost of Capital and Risk Calculator (ICCRC). I review the current practice in estimating the cost of capital and show how the ICCRC works. Most of the discussion focuses on the Excel version which is available in https://www.duke.edu/~charvey.

A long-standing problem in finance is the calculation of the cost of capital in international capital markets. There is widespread disagreement, particularly among practitioners of finance, as to how to approach this problem. Unfortunately, many of the popular approaches are ad hoc and, as such, difficult to interpret. The ICCRC provides alternative methodology which has strong economic foundations.

2. Cost of Capital: The Current Practice

There are remarkably diverse ways to calculate country risk and expected returns. The risk that I will concentrate on is risk that is systematic. That is, this risk, by definition, is not diversifiable. Importantly, systematic risk will be rewarded by investors. That is, higher systematic risk should be linked to higher expected returns.

2.1 The World Capital Asset Pricing Model

A simple, and well known, approach to systematic risk is the Capital Asset Pricing Model of the Sharpe (1964), Lintner (1965) and Black (1970). This model was initially presented and applied to U.S. data. The classic empirical studies, such as Fama and MacBeth (1973), Gibbons (1982) and Stambaugh (1982) presented some evidence in support of the formulation. The original formulation defined systematic risk as the contribution to the variance of a well-diversified market portfolio (the beta). The market portfolio was assumed to be the U.S. market portfolio. This model was first applied in an international setting by Solnik (1974a,b, 1977). The market is no longer the U.S. market portfolio but the world market portfolio.

The evidence on using the beta factor as a country risk measure in an international context is mixed. The early studies find it difficult to reject a model that relates average beta risk to average returns. For example, Harvey and Zhou (1993) find it difficult to reject a positive relation between beta risk and expected returns in 18 markets. However, when more general models are examined, the evidence against the model becomes stronger. Harvey (1991) presents evidence against the world CAPM when both risks and expected returns are allowed to change through time. Ferson and Harvey (1993) extend this analysis to a multifactor formulation that follows the work of Ross (1976) and Sharpe (1982). Their model also allows for dynamic risk premiums and risk exposures.

The bottom line for these studies is that the beta approach has some merit when applied in developed markets. The beta, whether measured against a single factor or against multiple world sources of risk, appears to have some ability to discriminate between expected returns. The work of Ferson and Harvey (1994, 1995, 1999) is directed at modeling the conditional risk functions for developed capital markets. They show how to introduce economic variables, fundamental measures, and both local and worldwide information into dynamic risk functions. However, this work only applies to 21 developed equity markets.

2.2 World Models Applied to Developing Markets

One might consider measuring systematic risk the same way in emerging as well as developed markets. Harveys (1995) study of emerging market returns suggests that there is no relation between expected returns and betas measured with respect to the world market portfolio. A regression of average returns on average betas produces an R-square of zero. Harvey documents that the country variance does a better job of explaining the cross-sectional variation in expected returns.

Indeed, the evidence in Harvey (1995) shows that, over the 1985-1992 period, the pricing errors are positive in every country in the IFC database. This implies that the model is predicting too low of an expected return in each country. In other words, the risk exposure as measured by the world model is too low to be consistent with the average returns.

One interpretation of Harvey (1995) is that the prices in emerging markets were too high and the model was correct. That is, the positive pricing error means that the model expected return was much lower than the realized return. Harvey (2000) revisits this analysis after significant adjustments in emerging market stock price levels after various financial crises. Here the CAPM model fares better. However, his evidence also shows that variance rather than beta does a better job of explaining returns across different emerging markets. This is clear evidence against the CAPM formulation.

2.3 The Country Spread Model (Goldman Model)

The following problem exists when applying a world CAPM to individual stocks in emerging markets. When regressing the company return (measured in U.S. dollars) on the benchmark return (either U.S. portfolio or the world portfolio), the beta is either indistinguishable from zero or negative. Given the correlations between many of the emerging markets and the developed markets are low and given the evidence in Harvey (1995a,b), it is no surprise that the regression coefficients (betas) are small. The implication is that the cost of capital for many emerging markets is the U.S. risk free rate or lower. This, of course, is a problematic conclusion. Importantly, the fitted cost of capital is contingent on the market examined being completely integrated into world capital markets. If this is not the case, then one has reason not to put much faith in the fitted cost of capital from the CAPM.

The following is a popular modification used by a number of prominent investment banks and consulting firms. A regression is run of the individual stock return on the Standard and Poors 500 stock price index return. The beta is multiplied by the expected premium on the S&P 500 stock index. Finally, an additional factor is added which is sometimes called the country spread. The spread between the countrys government bond yield for bonds denominated in U.S. dollars and the U.S. Treasury bond yield is added in. The bond spread serves to increase an unreasonably low cost of capital into a number more palpable to investment managers. For the details of this procedure, see Mariscal and Lee (1993).

There are many problems with this type of model. First, the additional factor is the same for every security even though different companies might have different exposures to country-specific risk. Second, this factor is only available for countries whose governments issue bonds in U.S. dollars. Finally, there is no economic interpretation to this additional factor. In some way, the bond yield spread represents an ex ante assessment of a country risk premium that reflects the credit worthiness of the government. However, beyond this, it is difficult to know how to fit this factor into a cost of capital equation. Most importantly, the premium we attach to debt is different than the premium attached to equity. It doesn't seem right to assume, for example, that the credit spread on a company's rated debt is the risk premium on the equity.

There is another version of the Goldman model. In this alternative version, which is focused on segmented capital markets, the traditional beta (covariance of market with S&P 500 divided by the variance of the S&P 500) is replaced by a modified beta. The modified beta is the ratio of the volatility of the market to the volatility of the S&P 500. Since the volatility is the segmented market is much greater than the covariance with the world, this serves to jack up the beta. It produces a higher risk premium. However, there is no economic foundation for such an exercise. Further, it is difficult to assess how well this fits the data.

2.4 The CSFB Model

Hauptman and Natella (1997) have proposed a model for the cost of equity in Latin America. Their model is hard to explain. Consider the equation:

E[r_i]=RF_i + Beta_i*K_i

where E[r_i] is the expected cost of capital; RF_i is the stripped yield of a Brady bond, Beta_i is the covariance of a particular stock with the broad based local market index, E[r_US-RF_US] is the U.S. risk premium, A_i is the coefficient of variation in the local market divided by the coefficient of variation of the U.S. market (where coefficient of variation is the standard deviation divided by the mean) and K_i is an adjustment factor to allow for the interdependence between the riskfree rate and the equity risk premium. In their application, Hauptman and Natella assume that K=0.60.

So you can see why this one is hard to explain. It has some similarity to the CAPM if we ignore the A and the K. However, the beta is measured against the local market return and the beta is multiplied by the risk premium on the U.S. market - which is not intuitive. Multiplying by the ratio of coefficients of variation is the same as multiplying by the ratio of the standard deviation of the local market to the standard deviation of the U.S. market - which is similar to the to the Goldman modified beta. You then need to multiply again by the ratio of the average return in the U.S. divided by the average return in the local market. In a way the average return in the U.S. is squared in this unusual formula.

This model is a perfect example of the confusion that exists in measuring the cost of capital.

2.5 The Ibbotson Model

Ibbotson offers a number of different models to its customers. One early model was a hybrid of the world capital asset pricing model. The securitys return minus the risk free rate is regressed on the world market portfolio return minus the risk free rate. The beta times the expected risk premium is calculated. An additional factor is also included. In this model, the additional factor is one half the value of the intercept in the regression. Half the value of the intercept plays a similar role as country spread in the previous model. The beta times the expected risk premium is too low to have credibility. When the intercept is added, this increases the fitted cost of capital to a more reasonable level. The evidence in Harvey (1995a,b) suggests that the intercept is almost always positive.

The advantage of this model is that it can be applied to a wider number of countries (i.e. you do not need government bonds offered in U.S. dollars). The intercept could be proxying for some omitted risk factor. However, there is no formal justification for including half the intercept. Why not include 100% or 25%? The best way to justify this model is in terms of Bayesian shrinkage. One might have a prior that the model is correct. In implementing the model going forward, the pricing error (intercept) is shrunk. Alternatively, one can think of two competing models: the average return and the CAPM. Adding half the intercept value, effectively averages the predictions of these two models.

2.6 Equity and bond premiums

Damodaran (1999) offers a novel approach to estimating the equity risk premium in emerging markets. His formula is

Country equity premium_i= Sovereign yield spread_i x (s_{i. Equity} s_i,Bonds

In contrast to the model that just additively includes the soveriegn yield spread, this model modifies the spread by multiplying by the ratio of equity to bond return volatility.

For this model to be operational, a country needs an equity market and a U.S. dollar sovereign bond market.

2.7 The Erb-Harvey-Viskanta Model Implemented in the ICCRC

This model specifies an external ex ante risk measure. Erb, Harvey and Viskanta (1996) require the candidate risk measure to be available for all 135 countries and available in a timely fashion. This eliminates risk measures based solely on the equity market. This also eliminates measures based on macroeconomic data that is subject to irregular releases and often-dramatic revisions. They focus on country credit ratings.

The country credit ratings source is Institutional Investor's semi‑annual survey of bankers. Institutional Investor has published this survey in its March and September issues every year since 1979. The survey represents the responses of 75‑100 bankers. Respondents rate each country on a scale of 0 to 100, with 100 representing the smallest risk of default. Institutional Investor weights these responses by its perception of each bank's level of global prominence and credit analysis sophistication [see Shapiro (1994) and Erb, Harvey and Viskanta (1994, 1995)].

How do credit ratings translate into perceived risk and where do country ratings come from? Most globally oriented banks have credit analysis staffs. Their charter is to estimate the probability of default on their bank's loans. One dimension of this analysis is the estimation of sovereign credit risk. The higher the perceived credit risk of a borrower's home country, the higher the rate of interest that the borrower will have to pay. There are many factors that simultaneously influence a country credit rating: political and other expropriation risk, inflation, exchange‑rate volatility and controls, the nation's industrial portfolio, its economic viability, and its sensitivity to global economic shocks, to name some of the most important.

The credit rating, because it is survey based, may proxy for many of these fundamental risks. Through time, the importance of each of these fundamental components may vary. Most importantly, lenders are concerned with future risk. In contrast to traditional measurement methodologies, which look back in history, a credit rating is forward looking.

The idea in Erb, Harvey and Viskanta (1996) is to fit a model using the equity data in 47 countries and the associated credit ratings. Using the estimated reward to credit risk measure, they forecast out-of-sample the expected rates of return in the 88 which do not have equity markets.

Should Country Risk Go in the Numerator or the Denominator?

In all of the models, the expected cost of capital (denominator) is increased to take into account of country risk. Traditional capital budgeting tools (in the U.S.) have suggested that the default probabilities should be incorporated into the cash flows (numerator). In the context of the U.S., I agree with this. That is, give the U.S. has little country risk, the idiosyncratic or company specific probabilities of bankruptcy should be reflected in the cash flows.

When we move offshore and especially to emerging markets, we should modify our methodology. I believe that the best assessment of default or traumatic event probabilities for a country is reflected in country ratings. So I adjust the denominator for the countrywide effects. The cash flows can be further adjusted to reflect company specific probabilities of bankruptcy (over and above what is induced by what happens in the country as a whole).

In the end, it does not matter how you do the exercise. A strategy that I have not pursued, but could pursue, is to back out the probability of crisis events from my discount rate. This probability could be used in Monte Carlo simulations, e.g. Crystal Ball, of the cash flows. As mentioned, it does not really matter how you do this, you will get the same present value. I find it more intuitive to keep all of the country specific information in the denominator and the company specific information in the numerator of the project evaluation process.

Let's consider a simple example. Suppose that you are examining a project in an emerging market that is in industry 'A'. We know if industry 'A' is located in the U.S., we would use a discount rate of 10%. Now, we evaluate the project in the emerging market. The expected cash flows are $100 per year forever (to keep the math simple). The IICCR says the country discount rate should be 20% and further suppose that the particular industry is reflective of the average risk in that country. The value is $100/.20=$500.[1] Now suppose you wanted to do some type of Value at Risk analysis. You would need to simulate the cash flows and the discount rate - which would be complicated. An alternative is to use the lower discount rate, 10%, but adjust the cash flows downward by the same factor. We get the same present value. In this case, we adjust the discount rate down 50% and the cash flows down 50%, so $50/.10=$500. Here, we have used the ICCRC to back out the discount factor that should be applied to cash flows that reflects the country risk. Note that in the first method, the $100 cash flows reflected the specific risks faced by the particular firm. Note that in the second method, the $50 cash flow reflects both the specific as well as the countrywide risks in the cash flows.

3. The Evidence

3.1 The Test Sample

Erb, Harvey and Viskanta (1996) analyze equity data from 47 national equity markets. Morgan Stanley Capital International (MSCI) publishes 21 of the indices, and the International Finance Corporation (IFC) of the World Bank publishes the other 26 indices. They treat the MSCI national equity indices as developed market returns and the IFC indices as emerging market returns. The test sample began in September 1979 and ends in March 1995. Twenty‑eight of the country indices existed at the beginning of this analysis. They added country indices to the analysis during the month that they were first introduced by either MSCI or the IFC.

As an illustration of the failure of traditional models, consider Figures 1 (full sample) and 2 (in the 1990s). These figures present average returns against the beta of the capital asset pricing model. There should be a positive relation -- higher beta implies higher return. There is no relation. The CAPM fails when applied to the countries in our sample. It is important to understand why.

The beta is an appropriate ex ante measure of risk if:

investors hold a diversified world market portfolio (i.e. no home bias)

the measured world market portfolio is a true representation of the value weighted world wealth

the market is integrated into world capital markets

expected returns and risk are constant

investors only care about expected returns and variance (no preference for skewness).

Even in the group of 47 equity markets, there are strong reasons to believe that conditions one, three and four do not hold.

3.2 Erb-Harvey-Viskanta specification

The idea of the Erb, Harvey and Viskanta (1996) is to fit:

where R is the semi-annual return in U.S. dollars for country j, Log(CCR) is the natural logarithm of the country credit rating which is available at the end of March and the end of September each year, time is measured in half years and e is the regression residual. They estimate a time-series cross-sectional regression by combining all the countries and credit ratings into one large model. In this sense, the coefficient is the reward for risk. Consistent with asset pricing traditions, this reward for risk is worldwide -- it is not specific to a particular country.

It is important to use the log of the credit rating. A linear model may not be appropriate. That is, as credit rating gets very low, expected returns may go up faster than a linear model suggests. Indeed, at very low credit ratings in a segmented capital market, such as the Sudan, it may be unlikely that any hurdle rate is acceptable to the multinational corporation considering a direct investment project.

Convincing evidence is presented in Erb, Harvey and Viskanta (1996) about the fit of the credit rating model. They find that higher rating (lower risk) leads to lower expected returns. Figure 3 shows a clear negative relation. It should be noted that the R-square in the 1990s is 30% which is about as good as you can get - even in the U.S. market with the best multifactor model!

There is also a linkage to the country-spread model. Erb, Harvey and Viskanata (1998) find that there is an 81% correlation between the country ratings and the sovereign yield spreads (U.S. dollar bonds issued in emerging markets minus U.S. Treasury yields). So, the credit ratings pick up the country risk reflected in these spreads but optimally fit the model to the current data.

4. Extensions

4.1 Volatility and correlation

The ICCRC provides a number of other relevant pieces of information. The program is calibrated to deliver, in addition to the cost of capital, the expected volatility (annualized standard deviation) and the expected correlation of the market with the U.S. market. Both the volatility and correlation are relevant for Monte Carlo analysis of expected cash flows from the project.

4.2 Payback

The ICCRC also presents some analysis of payback. This is the way to think of the problem. Suppose the expected return on the project is 15%. What is the probability that you will achieve 15% or greater in exactly one year? Answer 50%. [Note there is a 50% probability of achieving less than 15%] This is just the definition of the expected value or the mean. Lets change the question. What is the probability that the cumulative return is 15% over a two year period? Answer much higher than 15% because you have more time to get the positive returns.

Using the volatility and expected return, the ICCRC allows the user to specify the level of return (say doubling your investment or 100% return) and allows the user to specify the level of confidence in the prediction. The program solves for the number of years it takes to fulfill the criteria.

4.3 Anchoring

The customized Excel implementation of the ICCRC allows the corporation to anchor their cost of capital to their current U.S. rate. The user is prompted for the U.S. equity premium (expected return over and above the U.S. 10-year bond yield) and all other countries are calibrated to the U.S. rate. Graham and Harvey (2003) provide recent evidence that this risk premium is approximately 3.8% measured over a 10-year horizon (see Figure 4). This is important because the model has been calibrated over a particular sample. The average returns during this sample may be higher than the historical average over longer samples. In effect, by inputting the U.S. cost of capital, I allow the user to put their ex ante estimate of the future risk premium.

4.4 Using the ICCRC

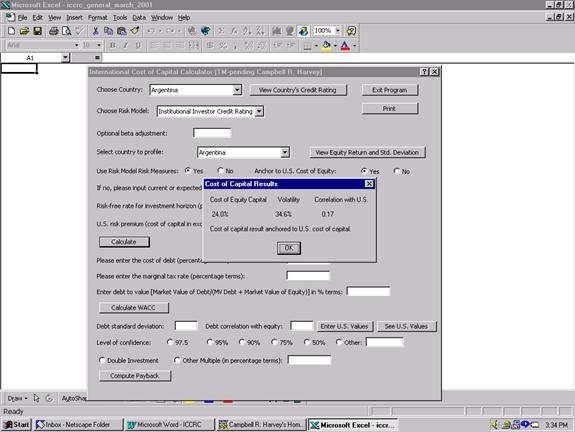
Appendix A provides an example Excel screen. The input fields are explained below:

Choose country: User can choose, from a drop down list, one of 135 countries.

Choose risk model: Currently, the user can only choose, Institutional Investors Country Credit Ratings. However, I also have information on Euromoneys Country Credit Ratings, the International Country Risk Guides Economic, Political, Financial or Composite Risk Ratings which is all available on request.

Outputs: The user can request, expected cost of capital, expected volatility and expected correlation with the U.S. While not included in the spreadsheets, I have also extended the analysis to a multiyear basis. In this model, one supplies the entire term structure of interest rates. Hurdle rates are calculated from years one to five. The multiyear rates are generally lower due to a time-diversification factor..

Use On-Line Risk Measures: This yes/no button allows the user to input their own assessment of the risk ratings. Otherwise the historical ratings are used. In the appendix example, there would be a good reason to override the March 2001 rating for Argentina given that the country is currently in a crisis.

Calculate: Processing button. Will display in a box the expected cost of capital, volatility and correlations.

WACC: The program will also calculate the weighted average cost of capital. The user must supply the cost of debt, the marginal tax rate and the debt to value ratio. Press calculate WACC and the WACC is delivered.

Payback: This determines how long it should take (at a given level of confidence) to multiply the investment by a particular factor. If the user has included debt in the calculation, the user must enter the debt standard deviation and correlation with equity. Alternatively, you could use U.S. values that can be obtained by pressing the button enter U.S. values.

Level of Confidence: The user can choose the confidence level for the payback.

Investement Multiple: The user can choose the hurdle. Note that this is a cumulative hurdle. Double investment means 100% return.

Compute Payback: Processing button for the payback analysis

References

Black, Fischer, 1972, Capital market equilibrium with restricted borrowing, Journal of Business 45, 444‑455.

Damodaran, Aswath, 1999, Estimating equity risk premiums, Unpublished working paper, New York University, New York, NY.

Erb, Claude, Campbell R. Harvey and Tadas Viskanta, 1994, Forecasting international equity correlations, Financial Analysts Journal, November‑December, 32‑‑45.

Erb, Claude, Campbell R. Harvey and Tadas Viskanta, 1995, Country risk and global equity selection, Journal of Portfolio Management, 21, Winter, 74‑‑83.

Erb, Claude, Campbell R. Harvey and Tadas Viskanta, 1996, Expected returns and volatility in 135 countries, Journal of Portfolio Management (1996) Spring, 46-58.

Erb, Claude, Campbell R. Harvey and Tadas Viskanta, 1998, Country Risk in Global Financial Management, Research Foundation of the AIMR.

Ferson, Wayne E. and Campbell R. Harvey, 1991, The variation of economic risk premiums, Journal of Political Economy 99, 285‑‑315.

Ferson, Wayne E., and Campbell R. Harvey, 1993, The risk and predictability of international equity returns, Review of Financial Studies 6, 527‑‑566.

Ferson, Wayne E., and Campbell R. Harvey, 1994a, Sources of risk and expected returns in global equity markets, Journal of Banking and Finance 18, 775‑‑803.

Ferson, Wayne E., and Campbell R. Harvey, 1994b, An exploratory investigation of the fundamental determinants of national equity market returns, in Jeffrey Frankel, ed.: The Internationalization of Equity Markets, (University of Chicago Press, Chicago, IL), 59‑‑138.

Graham, John R. and Campbell R. Harvey, 2003, Expectations of equity risk premia, volatility and asymmetry, Unpublished working paper, Duke University, Durham, NC.

Harvey, Campbell R., 1991a, The world price of covariance risk, Journal of Finance 46, 111‑‑157.

Harvey, Campbell R., 1991b, The term structure and world economic growth, Journal of Fixed Income 1, 4‑‑17.

Harvey, Campbell R., 1991c, The specification of conditional expectations, Working paper, Duke University, Durham, NC.

Harvey, Campbell R., 1993a, Portfolio enhancement using emerging markets and conditioning information, in Stijn Claessens and Shan Gooptu, Eds., Portfolio investment in developing countries (Washington: The World Bank Discussion Series, 1993, pp. 110‑‑144).

Harvey, Campbell R., 1993b, Conditional asset allocation in emerging markets, Working paper, Duke University, Durham, NC.

Harvey, Campbell R., 1995a, Predictable risk and returns in emerging markets, Review of Financial Studies 8, 773‑‑816.

Harvey, Campbell R., 1995b, The risk exposure of emerging markets, World Bank Economic Review, 9, 19‑‑50.

Harvey, Campbell R., 1995c, The cross‑section of volatility and autocorrelation in emerging equity markets, Finanzmarkt und Portfolio Management 9, 12‑‑34.

Harvey, Campbell R., 2000, Drivers of expected returns in international markets, Emerging Markets Quarterly 4, 32-49.

Hauptman, Lucia and Stefano Natella, 1997, The cost of equity in Latin America: The eternal doubt, Credit Swisse First Boston, Equity Research, May 20.

Mariscal, Jorge O. and Rafaelina M. Lee, 1993, The valuation of Mexican stocks: An extension of the capital asset pricing model, Goldman Sachs, New York.

Ross, Stephen A., 1976, The arbitrage theory of capital asset pricing, Journal of Economic Theory 13, 341‑‑360.

Ross, Stephen A., 1989, Information and volatility: The no‑arbitrage martingale approach to timing and resolution irrelevancy, Journal of Finance 44, 1‑‑17.

Sharpe, William, 1964, Capital asset prices: A theory of market equilibrium under conditions of risk, Journal of Finance 19, 425‑‑442.

Solnik, Bruno, 1974a, An equilibrium model of the international capital market, Journal of Economic Theory 8, 500‑‑524.

Solnik, Bruno, 1974b The international pricing of risk: An empirical investigation of the world capital market structure, Journal of Finance 29, 48‑‑54.

Solnik, Bruno, 1977, Testing international asset pricing: Some pessimistic views, Journal of Finance 32 (1977), 503‑‑511.

Solnik, Bruno, 1983, International arbitrage pricing theory, Journal of Finance 38, 449‑‑457.

Figure 1

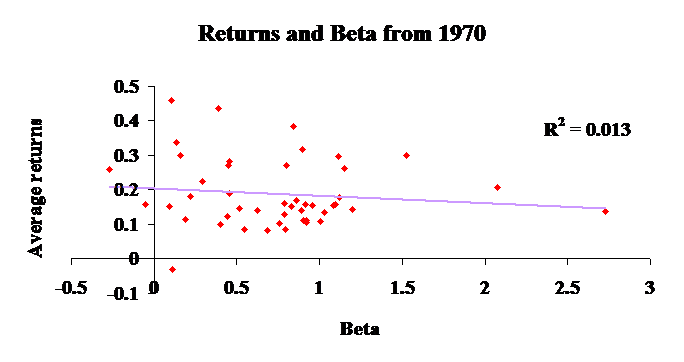
Notice the relation goes the wrong way. Higher risk (beta) is associated with lower returns.

Figure 2

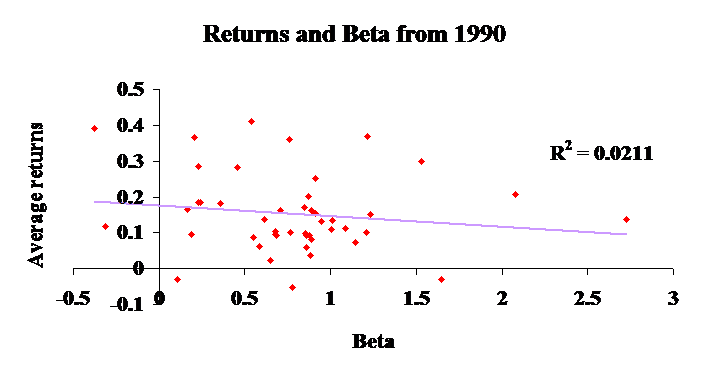
Even, if we use more recent data, the risk-return relation goes the wrong way.
Figure 3

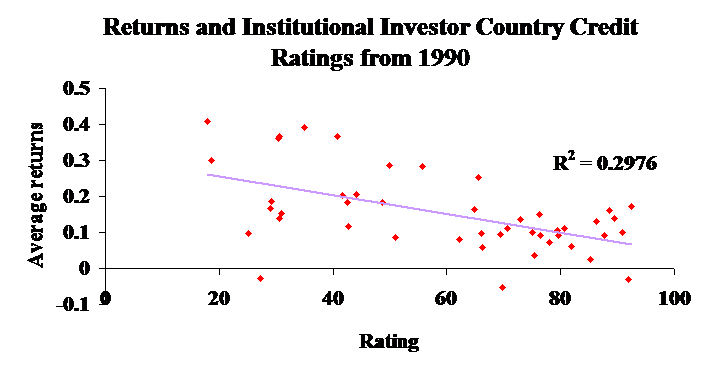
Notice that lower rating means higher risk and associated higher expected return.

Figure 4

10-year Risk Premium based on Graham and Harvey (2003) survey of CFOs.
Appendix A: Sample IICRC Excel Screen

Inputs: (i) Select country, (ii) anchor to your view of U.S. risk premium, (iii) current risk free rate, (iv) your view of U.S. risk premium

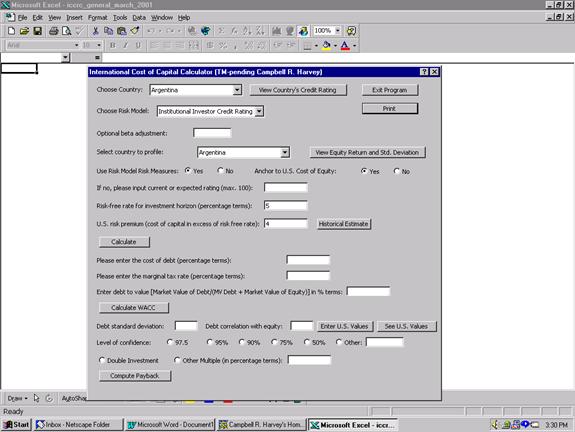
Appendix A: Sample IICRC Excel Screen (continued)

Outputs: Press Calculate button and obtain (i) expected return in U.S. dollars, (ii) expected volatility and (iii) expected correlation with the world market portfolio.