Plokščiųjų figūrų simetrijų grupės

Plokščiųjų figūrų simetrijų grupės

Sakykime, kad plokštumoje turime kažkoki¹ figūr¹ . Plokštumos transformacija f, kuria figūra atvaizduojama į save vadinama figūros simetrija. Jei Jei . Aišku, kad id:

Iš čia matyti, kad figūros simetrijų aibė yra grupė kompozicijos atžvilgiu. Ši grupė vadinama figūros simetrijų grupe.

Egzistuoja figūros, kurių simetrijų grupė susideda iš vienos tapatingosios transformacijos, pvz.: bet koks trikampis ( nelygiašonis, nelygiakraštis). Sakoma, kad tokios figūros   neturi simetrijų. Lygiašonis trikampis turi simetrijų grupź iš dviejų elementų. Jeigu tiesė l jo pagrindo vidurio statmuo, tai jo simetrijos grupź sudaro dvi transformacijos

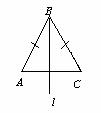
Pav. 1

Jeigu ašinė simetrija yra figūros simetrijų grupės elementas, tai tiesė l yra vadinama figūros simetrijos ašimi, o figūra vadinama simetriška tiesės l atžvilgiu.

Kita figūra turinti simetrijų grupź iš dviejų transformacijų, tai lygiagretainis.

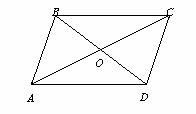
Pav. 2

Jo simetrijų grupź sudaro dvi transformacijos: tapatingoji ir , t.y. , čia O yra įstrižainių sankirtos taškas.

Jeigu centrinė simetrija priklauso figūros simetrijų grupei, tai figūra vadinama simetriška taško O atžvilgiu, o taškas O yra vadinamas jos simetrijos centru. Sakoma, kad taškas O yra figūros n-tosios eilės simetrijos centras, jeigu figūros simetrijų grupei priklauso posūkiai apie tašk¹ O, kampais , , čia k = 1, 2, 3,…, n. Pvz.: kvadrato centras yra 4 – osios eilės (n = 4) simetrijos centras.

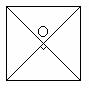
Pav. 3

Bet koks taisyklingasis n – kampis turi n – tos eilės simetrijos centr¹, t.y. apibrėžto ir įbrėžto apskritimo centr¹. Egzistuoja figūros turinčios be galo daug simetrijų. Pvz.: juosta tarp dviejų lygiagrečių tiesių. Jei tiesė l eina per jų vidurį, tai juostų simetrijų grupė yra tokia .

Apskritimas irgi turi be galo daug simetrijų.

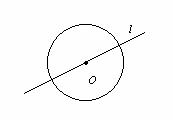
Pav. 4

.

Be to iš judesių savybių išplaukia, kad jeigu figūra turi dvi statmenas simetrijos ašis, tai tų ašių sankirta yra jos simetrijos centras. Jeigu yra simetrijos ašys, tai . O – simetrijos centras, nes .

TEOREMA. Taisyklingojo n – kampio simetrijų grupź sudaro 2n transformacijų.

Įrodymas. Sakykime, kad A yra taisyklingojo n – kampio viršūnė, o B ir C gretimos viršūnės.

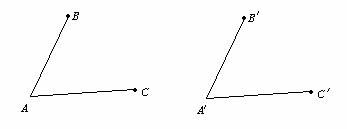
Pav. 5

Tarkime, kad kokia nors transformacija f: viršūnė A atvaizduojama i viršūnź . Nesunku patikrinti, kad jeigu transformacija f daugiakampį atvaizduoja į jį patį, tai viršūnź atvaizduoja į viršūnź. Tarkim trikampis ABC turi atsivaizduoti į jam lygų trikampį. Tuomet jeigu taško A vaizdas bus kokios tai kraštinės viduje, o ne viršūnėje, tai viršūnių B ir C vaizdai nebus daugiakampio kraštinėse.

Jeigu ir yra viršūnės gretimos viršūnės, tai gauname, kad trikampiai ABC ir yra lygūs ir lygiašoniai. Galimi du atvejai:

Kadangi du lygūs trikampiai pilnai apibrėžia judesį, tai mes gavome du judesius ir , kurie n – kampį atvaizduoja patį į save.

Kadangi A yra bet kuri iš viršūnių, o kiekvienai iš viršūnių egzistuoja dvi daugiakampio simetrijas, tai iš čia matyti, kad taisyklingasis n – kampis turi 2n simetrijų.

Įrodyti, kad daugiau tokių simetrijų nebus, pakanka pasinaudoti tuo, kad viršūnė atvaizduojama į viršūnź ir gaunamos vienas iš jau nagrinėtų judesių.