| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
OPROCENTOWANIE SKŁADANE
Zasada oprocentowania składanego (złożonego) polega na tym, że po upływie każdego ustalonego okresu odsetki dodaje się do kapitału i w następnym okresie oblicza się odsetki od kapitału o zwiększonej wartości. Mówimy wówczas, że odsetki podlegają kapitalizacji.
Założenia: Okresem kapitalizacji jest okres podstawowy
(zwykle jeden rok) oraz ![]() .
.
Po pierwszym okresie kapitał wynosi ![]() , po drugim
, po drugim ![]() , po trzecim
, po trzecim![]() , itd. Wartość kapitału po upływie n okresów jest więc równa:
, itd. Wartość kapitału po upływie n okresów jest więc równa:
![]()
Czynnik (1+i) nazywamy czynnikiem oprocentowującym.
Odsetki za rok n-ty wynoszą
![]()
Wnioski
Przyszła wartość kapitału Kn jest funkcją czasu ..
Ciąg utworzony z wartości Kn dla n=0, 1, 2, jest ciągiem
Stopa efektywna dla n-tego okresu wynosi przy oprocentowaniu składanym
![]()
Wniosek
W oprocentowaniu składanym efektywna stopa procentowa jest .
PORÓWNANIE ZMIAN WARTOŚCI KAPITAŁU W CZASIE PRZY OPROCENTOWANIU PROSTYM I SKŁADANYM
|
oprocentowanie proste |
oprocentowanie składane |
|
|
przyrost absolutny |
funkcja |
funkcja |
|
przyrost względny |
funkcja |
funkcja |
KAPITALIZACJA ODSETEK W PODOKRESACH
Niech m oznacza liczbę
(częstotliwość) kapitalizacji odsetek w okresie podstawowym.
Stopę procentową i(m) nazywamy stopą
nominalną przy m-krotnej
kapitalizacji w ciągu okresu podstawowego, jeśli odsetki są
doliczane do kapitału przy stopie procentowej ![]() po każdej m-tej części okresu.
po każdej m-tej części okresu.
Przyszła wartość kapitału po n latach jest wyrażona wzorem
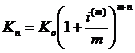
Z porównania (2.1) i (2.4) otrzymujemy wzór na stopę efektywną
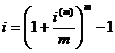
Twierdzenie
Skracanie okresu kapitalizacji odsetek powoduje .
Przy ustalonej stopie nominalnej d wyznaczymy graniczną wartość
kapitału Kn po n latach przy kapitalizacji odsetek prowadzonej
w sposób ciągły, tzn. przy ![]() .
.
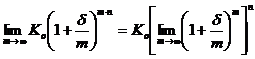
Ponieważ
![]() ,
,
to stosujemy podstawienie ![]() . Ponieważ
. Ponieważ ![]() , to także
, to także ![]() . Po podstawieniu otrzymujemy
. Po podstawieniu otrzymujemy
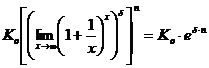 .
.
Wartość kapitału po n latach ciągłej kapitalizacji odsetek przy nominalnej stopie procentowej d jest więc dana wzorem
![]()
Stopę nominalną d przy kapitalizacji ciągłej nazywamy intensywnością (siłą) oprocentowania.
Biorąc pod uwagę wzory (2.1) i (2.6) można zapisać, że
![]()
Niech interesujący nas okres n lat składa się z k następujących po sobie podokresów o
długości ![]() takich, że
takich, że ![]() oraz w każdym podokresie stopa procentowa nie zmienia
się i w skali roku odpowiednio wynosi i1,
i2, , ik. Końcowa wartość
kapitału po n latach wyniesie więc
oraz w każdym podokresie stopa procentowa nie zmienia
się i w skali roku odpowiednio wynosi i1,
i2, , ik. Końcowa wartość
kapitału po n latach wyniesie więc
![]()
Stopę przeciętną wyznaczymy więc z równania
![]()
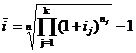
Wniosek
Do obliczenia przeciętnej stopy procentowej stosujemy formułę średniej ..
Znając przyszłą wartość kapitału Kn można wyznaczyć ze wzoru (2.1) początkową wartość Ko
![]()
Wartość Ko nazywamy zdyskontowaną wartością kapitału Kn na n lat wstecz.
Czynnik ![]() nazywamy czynnikiem
dyskontującym.
nazywamy czynnikiem
dyskontującym.
Jeśli w momencie t wartość kapitału wynosi K, to wartość aktualna w momencie t tego kapitału wynosi ![]() bez względu na to
czy t > t (oprocentowujemy kapitał), czy t < t (dyskontujemy
kapitał).
bez względu na to
czy t > t (oprocentowujemy kapitał), czy t < t (dyskontujemy
kapitał).
DYSKONTO HANDLOWE SKŁADANE
Niech d będzie efektywną stopą dyskontową niezależną od czasu.
Dyskontując kapitał Kn
o jeden okres wstecz otrzymujemy ![]() , o dwa okresy wstecz
, o dwa okresy wstecz ![]() , o trzy okresy wstecz
, o trzy okresy wstecz ![]() itd. Początkowa
wartość kapitału wynosi więc
itd. Początkowa
wartość kapitału wynosi więc
![]()
W przypadku kapitalizacji w podokresach d(m) oznacza nominalną stopę dyskontową,
tzn. dyskonto potrącane jest z kapitału przy stopie dyskontowej ![]() po każdej m-tej części okresu.
po każdej m-tej części okresu.
Początkowa wartość kapitału wynosi więc
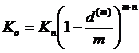
Porównując (2.10) i (2.11) otrzymujemy wzór na efektywną stopę dyskontową
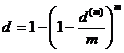
W oprocentowaniu składanym zachodzą następujące relacje między stopami
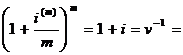
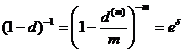
Stopa inflacji wyraża wzrost (spadek) przeciętnego poziomu cen towarów i usług w określonym czasie. Inflacja powoduje spadek (wzrost) siły nabywczej pieniądza.
Następujące stopy procentowe dotyczą okresu podstawowego
q stopa inflacji (jeżeli ceny wzrosły, to .., jeżeli ceny spadły, to ..,),
i stopa oprocentowania kapitału,
r rzeczywista stopa wzrostu wartości kapitału (po wyeliminowaniu czynnika inflacji).
Po upływie jednego okresu kapitał początkowy Ko będzie miał wartość:
nominalną Ko(1+i)
rzeczywistą ![]()
Posługując się stopą rzeczywistą r mamy Ko(1+r) = ![]() .
.
Otrzymujemy więc zależność między stopami ![]() , z której
można wyznaczyć
, z której
można wyznaczyć
![]()
lub
![]()
Uwaga
Rzeczywista stopa wzrostu wartości kapitału nie jest różnicą między stopą oprocentowania, a stopą inflacji.
Wnioski
Jeśli stopa inflacji jest dodatnia, to rzeczywista stopa wzrostu wartości kapitału jest . niż różnica stóp oprocentowania i inflacji.
Jeśli stopa inflacji jest większa od stopy oprocentowania, to rzeczywista stopa jest i rzeczywista wartość kapitału ..
Jeśli stopa inflacji jest ujemna, to rzeczywista stopa jest i rzeczywista wartość kapitału z powodu inflacji
Niech q1, q2, , qn będą stopami inflacji z kolejnych n okresów o jednakowej długości.
Stopę inflacji łącznie za n okresów obliczymy więc ze wzoru
![]()
Przeciętną stopę inflacji ![]() przypadającą na jeden okres
wyznaczymy z równania
przypadającą na jeden okres
wyznaczymy z równania
![]()
otrzymując
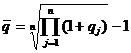
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1750
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved