| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
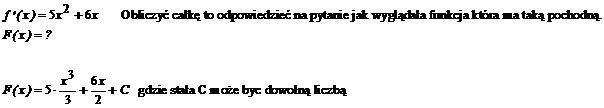
![]()
Wzory:
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
Przykład:
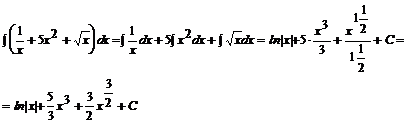
Przykład:
![]()
Przykład:
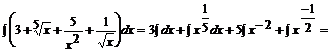
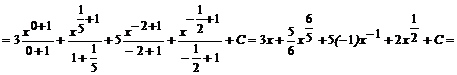
![]()
Przykład:
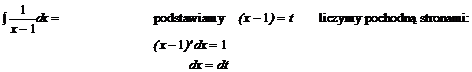
![]()
Przykład:
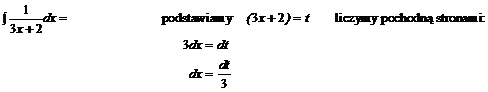
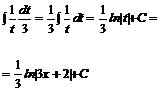
Przykład:
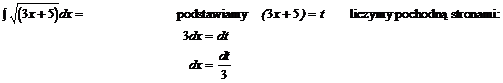
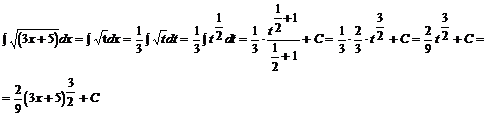
Przykład:
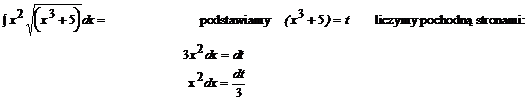
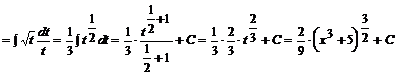
Uproszczenia możliwe w obliczeniach:
Uproszczenie 1.
Wyprowadzenie:
Rozwiążmy poniższy przykład:
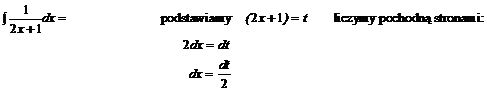
![]()
Uproszczenie 1.
Końcowy wzór:

Jeżeli w mianowniku jest funkcja a w liczniku jest pochodna tej funkcji to całka jest równa:
![]()

Przykład1: ![]()

Przykład2:
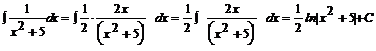
Uproszczenie 2.
Wyprowadzenie:
Rozwiążmy następujący
przykład: ![]()
Nie możemy zastosować poznanych wcześniej wzorów. Stosujemy metodę rozkładu na ułamki proste.
Sprowadzamy mianownik do postaci rozłożonej.
![]()
![]()
![]()
![]()

![]()
![]()
Gdyby wyrażenie: ![]()
można było przedstawić jako
sumę dwu wyrażeń ![]()
to można by było zastosować znane już wzory.
Zakładamy, że są takie wartości A i B które spełniają te wyrażenia. Dokonajmy więc przekształcenia takiej sumy wyrażeń:
![]()
czyli:
![]()
Jeżeli strony równania są równe przy jednakowych mianownikach, więc liczniki są też równe. Możemy więc napisać:
![]()
Obliczamy wartość A i B dla których równanie będzie prawdziwe. Aby x nie miał wpływu na wyrażenie musi być spełniony warunek : x(A+B) = 0
będzie to zawsze spełnione gdy: A + B = 0
Przy takim warunku całe wyrażenie ![]() będzie prawdziwe
gdy 2A+3B = 1
będzie prawdziwe
gdy 2A+3B = 1
Możemy napisać układ równań z których wyliczymy wartość A i B :
![]()
![]()
![]()
![]()
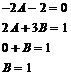
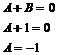
Całe nasze wyrażenie przybierze postać:
![]()
Uproszczenie 2.
Końcowy wzór:

![]()
Wzory:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
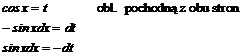
![]()
![]()
![]()
Przykład:
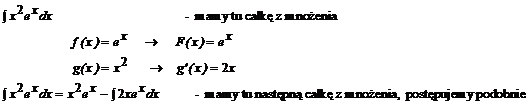
![]()
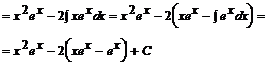
Przykład:
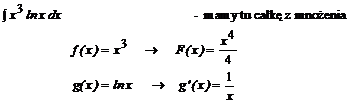
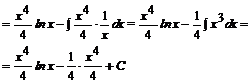
Przykład:
![]()
![]()
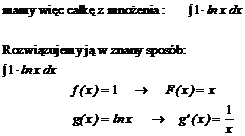
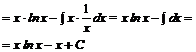
![]()
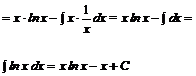
Przykład:
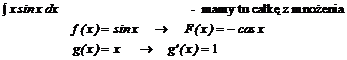
![]()

![]() Wzór do zapamiętania!
Wzór do zapamiętania!
Co to jest arctg? ![]()
![]()
Przykład:
![]()
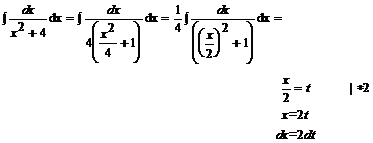
![]()
Przykład:
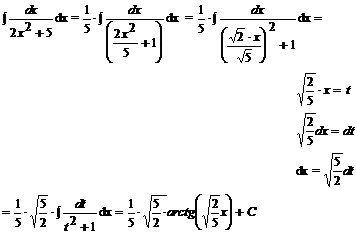
Matematyka.
Przykład:
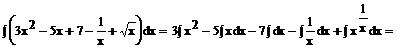
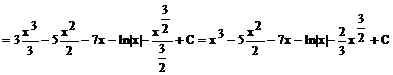
Przykład:
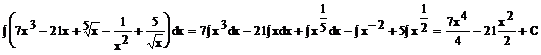
Przykład:
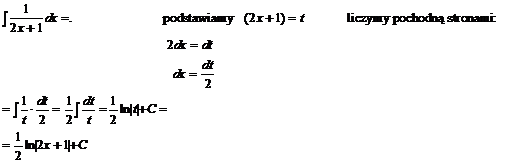
Przykład:
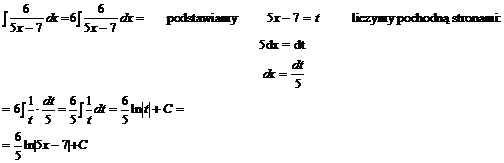
Przykład:
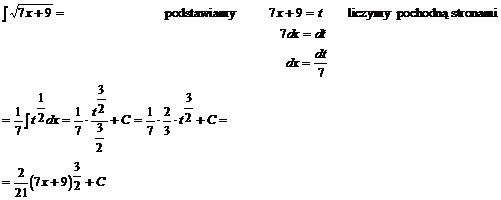
Przykład:
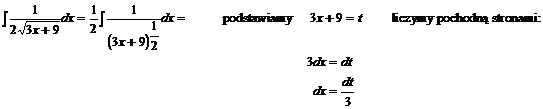
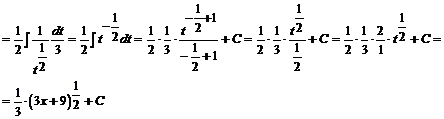
Przykład:
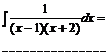 ? ? ? ? ????????
? ? ? ? ????????
![]()
![]()
Przykład:
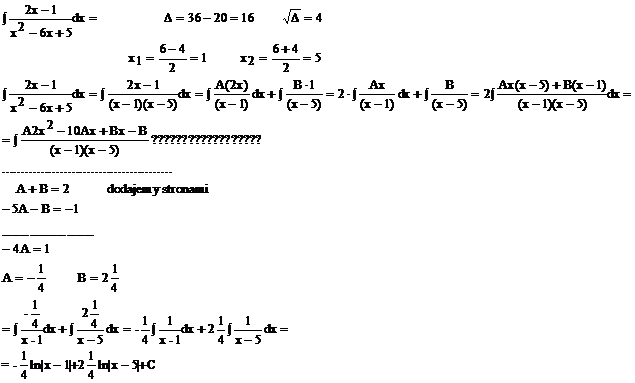
Przykład:
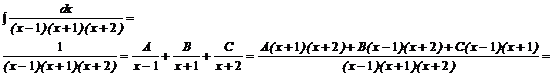
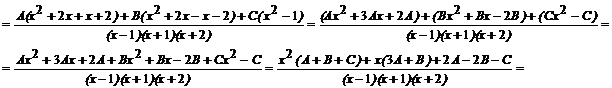
Jeżeli ułamki:
![]()
są równe to i liczniki tych ułamków są równe. Możemy więc napisać:
![]()
Obliczamy wartość A, B, C
![]() A
+ B + C = 0
A
+ B + C = 0
3A + B 0 = 0
2A - 2B - C = 1
Z drugiego równania obliczamy B:
B = -3A
![]() A -
3A C = 0
A -
3A C = 0
2A - 2(-3A) - C = 1
-2A +C = 0
8A - C = 1
6A = 1
A = 1/6
B = -3A = - 3(1/6) = - 1/2
B = - 1/2
A + B + C = 0
A + B = - C
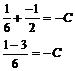
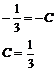
![]()
Nasze równanie przybierze więc postać:
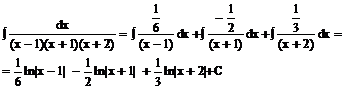
Przykład:
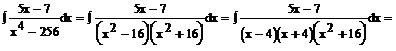
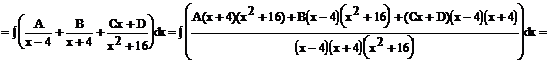
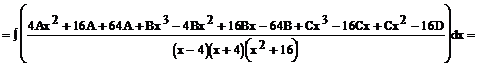
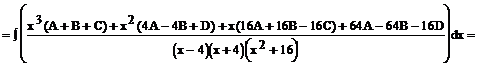
Aby obliczyć wartości A, B, C, D, piszemy układy równań:
![]()
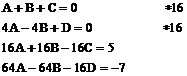
Dodajemy pierwsze i trzecie równanie :
![]()
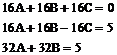
Dodajemy drugie i czwarte równanie :
![]()
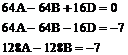
W wyniku tych działań otrzymujemy dwa równania:
![]()
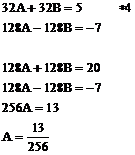
Z równania ![]() obliczamy B
obliczamy B
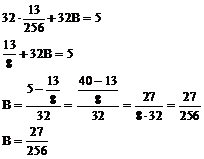
Z równania A + B + C = 0 obliczamy C
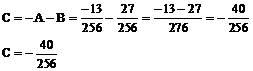
Z równania 4A - 4B + D = 0 obliczamy D
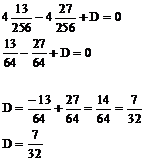
Podstawiamy obliczone wartości A, B, C, D do równania:
![]()
![]()
![]()
![]()
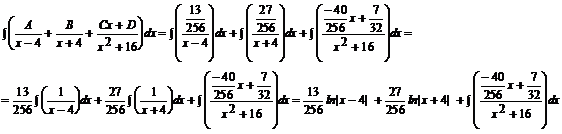
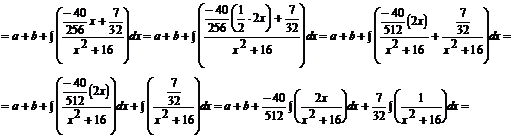
![]()
![]()
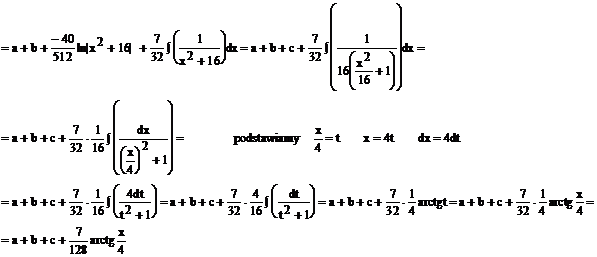
Przykład:
![]()
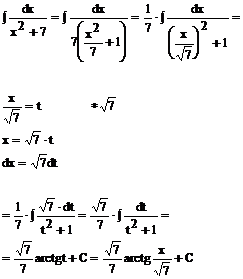
Przykład:
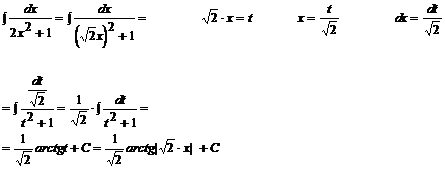
Przykład:
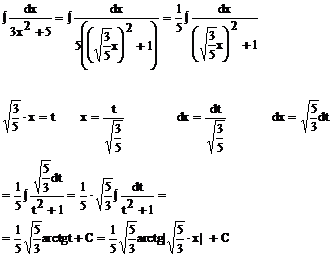
Przykład:
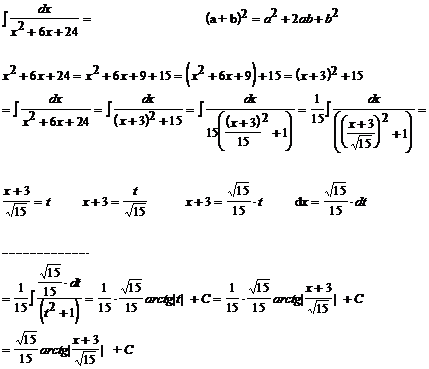
Powtórka: ![]()
Przykład:
![]() delta ujemna, do
rozwiązania należy wykorzystać inną metodę.
delta ujemna, do
rozwiązania należy wykorzystać inną metodę.
Wykorzystać można wzór: ![]()
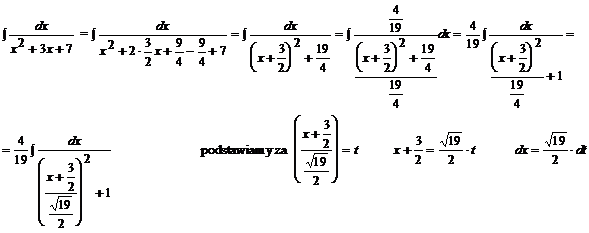
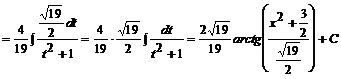
Przykład:
![]()
Przypomnienie wzoru: ![]()
pochodna z mianownika naszego przykładu
była by: ![]()
licznik z naszego przykładu jest : ![]()
aby doprowadzić go do postaci: ![]()
należy dokonać przekształcenia:
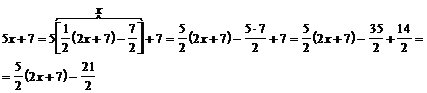
Wracamy do naszej całki:
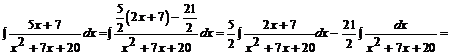
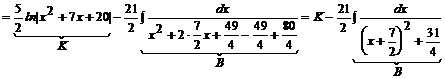
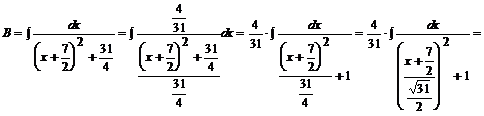
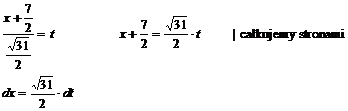
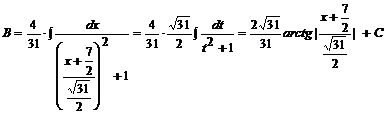
Przykład:
![]()
![]()
Wszystkie poznane do tej pory całki to całki nieoznaczone.
Całka oznaczona to całka dla której określa się przedział. Musi być różniczkowalna.

![]()
Przykład:
![]()
Przykład:
![]() podstawiamy:
podstawiamy: ![]()
dla ![]()
![]()
Przy metodzie podstawiania trzeba zmienić granice całkowania bo zmienia się zmienna.
Wracamy do przykładu: 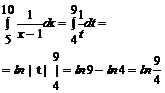
Twierdzenia: ![]()
![]()
![]()

P
![]() a b
a b
![]()
Przykład:
Mamy dwie
funkcje: 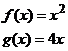
![]() x2
x2
![]()
4x
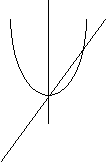
Obliczyć pole zawarte między jednym a drugim wykresem w obszarze między przecięciami się tych wykresów.
Wykresy przecinają się dla x który jest równy: ![]()
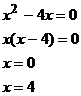
Pole będzie równe różnicy :
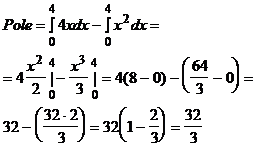
25.04.98 ćwiczenia Przykład:

![]()

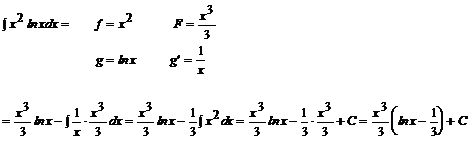
Przykład:
![]()
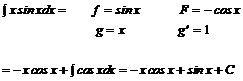
Przykład:

![]()
![]()
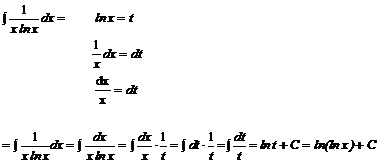
Przykład:

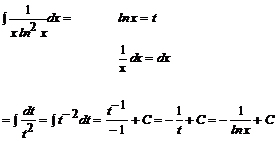
Przykład:
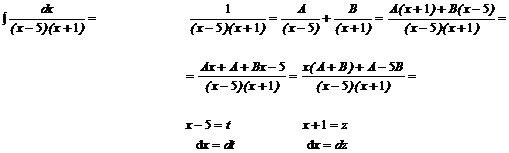
![]()
![]()
 (-1)
(-1) 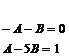
![]()
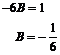
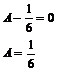
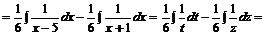
![]()
Przykład:
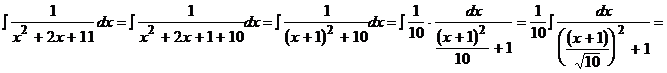
![]()
![]()
Przykład:
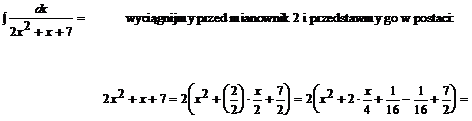
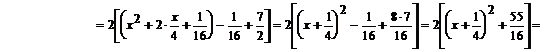
Podstawiamy do naszego przykładu:
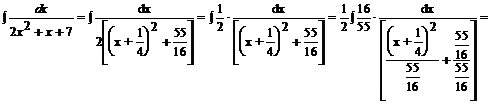
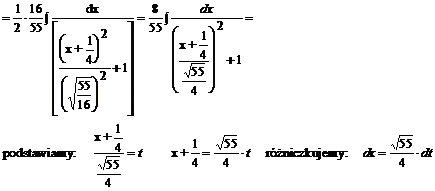
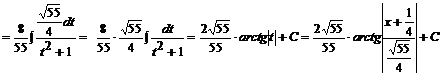
Przykład:
![]() zastosujemy
wzór
zastosujemy
wzór ![]()
Obliczamy pochodną mianownika: 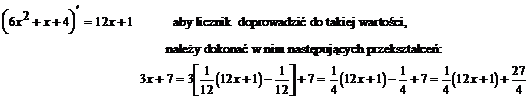
Podstawiamy obliczoną wartość w miejsce licznika:
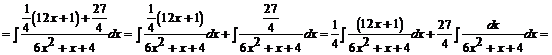
![]()
![]()
Rozpisujemy mianownik aby można było
zastosować wzór: ![]()
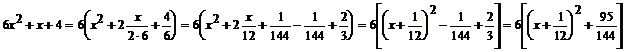
Wracamy do obliczeń całki:
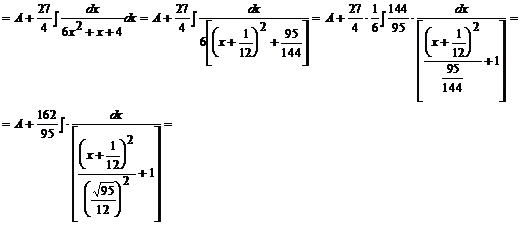
Podstawiamy:
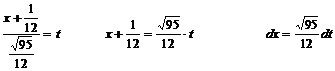
Wstawiamy to do przykładu:
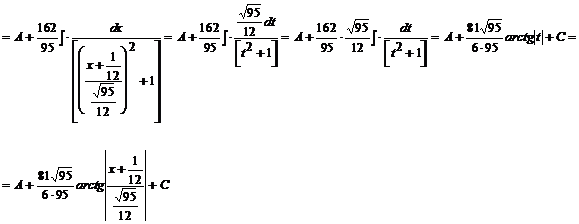
![]()
Rozwiązaniem ![]() jest:
jest:![]()
Przykład:
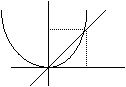
Obliczyć pole między wykresami
funkcji: ![]()
![]()
7
Obliczamy miejsca przecięcia się tych wykresów (wspólne wartości X dla obu wykresów):
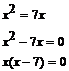
Dla ![]() oraz
oraz ![]() wykresy tych
funkcji przecinają się.
wykresy tych
funkcji przecinają się.
Pole między wykresami tych funkcji będzie równe różnicy całek oznaczonych tych funkcji dla przedziału 0,7
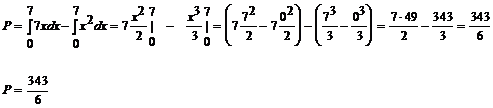
Przykład:
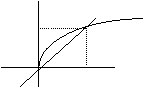
Obliczyć pole między wykresami
funkcji: ![]()
![]()
1/4
Obliczamy miejsca przecięcia się tych wykresów (wspólne wartości X dla obu wykresów):
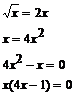
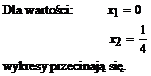
Pole między wykresami tych funkcji
będzie równe różnicy całek oznaczonych tych funkcji dla
przedziału ![]()
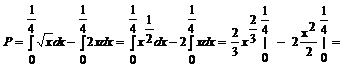
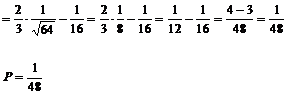
Wzory na obliczanie całek:
![]()
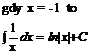
2. ![]()
3. ![]()
4. ![]()
5. Jeżeli w mianowniku jest funkcja a w liczniku jest pochodna tej funkcji to całka jest równa:
![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
![]()
![]()
![]()
![]()
![]()
Twierdzenia: 1. ![]()
2. ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1025
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved