| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Rachunek prawdopodobieństwa - podstawowe definicje.
Niech E będzie pewnym niepustym zbiorem - w dalszym ciągu będziemy go nazywać przestrzenią zdarzeń elementarnych. Elementy eIE będziemy nazywać zdarzeniami elementarnymi.
W E wyróżniamy pewną rodzinę S jego podzbiorów, spełniającą pewne warunki (omówione poniżej), które stwierdzają że S jest tak zwanym s-ciałem (lub inaczej: s-algebrą) podzbiorów przestrzeni E. Elementy A należące do S (AIS) nazywamy zdarzeniami losowymi lub po prostu - zdarzeniami. (Tak więc, w szczególności, zdarzenia losowe są podzbiorami zbioru E, zaś elementami zdarzeń losowych są zdarzenia elementarne.) Warunki definicji s-ciała możemy nieco nieściśle wyrazić stwierdzeniem, że na zdarzeniach możemy dokonywać operacji sumy, iloczynu, różnicy, dopełnienia, a także sumy i iloczynu przeliczalnej ilości zdarzeń i w wyniku nadal otrzymujemy zdarzenia. Dokładnie, S nazywamy s-ciałem podzbiorów przestrzeni E, jeżeli
(i) S 2E, tzn. A E gdy AIS
(ii) IS;
(iii) Jeżeli AiIS dla i=1,2,3, oraz A=A1 A2 A3 (suma przeliczalnej ilości zdarzeń), to AIS.
(iv) Jeżeli AIS, to A =EAIS
Jeżeli zbiór E jest skończony lub przeliczalny, to za S przyjmujemy na ogół rodzinę wszystkich podzbiorów przestrzeni E (S=2E). Jeżeli E jest zbiorem nieprzeliczalnym, to okazuje się, że aby w ogóle można było określić pewną funkcję prawdopodobieństwa (czyli tzw. miarę unormowaną) P na S, S nie może się składać ze wszystkich - lecz jedynie z niektórych podzbiorów przestrzeni E (zwanych niekiedy podzbiorami mierzalnymi). Ważnym, lecz nietrywialnym przykładem jest s-ciało zbiorów Borelowskich na prostej - jest to najmniejsze s-ciało zbiorów, do którego należą wszystkie przedziały otwarte (a w konsekwencji, wszystkie zbiory otwarte, a więc i wszystkie zbiory domknięte, dalej - przeliczalne przecięcia zbiorów otwartych, przeliczalne sumy zbiorów domkniętych itd.).
P - funkcja prawdopodobieństwa (miara unormowana) jest funkcją P:S <0,1>, spełniającą następujące warunki (stwierdzające w istocie, że P jest miarą unormowaną):
(i) P:S <0,1>, czyli P jest określone na zdarzeniach (czyli zbiorach A należących do S) i 0 P(A) 1 dla każdego AIS
(ii) P(
(iii) Jeżeli AiIS dla i=1,2,3, przy czym Ai Aj= dla i j (zbiory Ai są parami rozłączne), to P(A1 A2 A3 )= P(A1)+P(A2)+P(A3)+ (przeliczalna addytywność prawdopodobieństwa dla zbiorów parami rozłącznych)
(iv) P(E)=1.
Własności s-ciała (s-algebry) S oraz funkcji prawdopodobieństwa P.
|
S - rodzina zdarzeń losowych (s-ciało) |
P - prawdopodobieństwo (miara unormowana) na S |
|
1. S 2E, tzn. A E gdy AIS |
1. P:S < >, tzn. dla AIS P(A) |
|
IS - zdarzenie niemożliwe) |
2. P( |
|
3. EIS (E - zdarzenie pewne) |
3. P(E)=1 |
|
4. Jeżeli AiIS (i=1,2,3,), to A1 A2 A3 IS 4. Jeżeli AiIS (i=1,2,3,), to A1 A2 A3 IS W szczególności, własności 4 i 4 zachodzą dla skończonego ciągu zbiorów. |
4. Jeżeli AiIS (i=1,2,3,), to P(A1 A2 A3 P(A1)+P(A2)+P(A3)+ Uwaga. P(A1 A2)=P(A1)+P(A2)P(A1 A2); P(A1 A2 A3)= P(A1)+P(A2)+P(A3)+ P(A1 A2)P(A2 A3)P(A3 A1)+P(A1 A2 A3) |
|
5. Oczywiście, własność 4 zachodzi w szczególności dla zbiorów parami rozłącznych. Na odwrót, sumę dowolnego ciągu Ai można przedstawić w postaci sumy ciągu zbiorów parami rozłącznych Bi , gdzie B1=A1, B2=A2A1 , B3=A3(A1 A2) itd. |
5. Gdy AiIS (i=1,2,3,) są parami rozłączne, tzn. Ai Aj= dla i j, to P(A1 A2 A3 ) = P(A1)+P(A2)+P(A3)+ (w istocie po prawej stronie występuje suma szeregu nieskończonego) |
|
6. Gdy AiIS (i=1,2,3,) oraz A1 A2 A3 (ciąg wstępujący), to P(A1 A2 A3 )=lim P(An) ; 6 Gdy AiIS (i=1,2,3,) oraz A1 A2 A3 (ciąg zstępujący), to P(A1 A2 A3 )=lim P(An) . |
|
|
7. Jeżeli AIS, to A = E AIS |
7. P(A) = 1P(A) |
|
8. A,BIS, to A BIS |
8. P(A) P(B) P(A B) |
|
9. A, BIS, A B, to P(A) P(B). |
Definicja prawdopodobieństwa warunkowego: niech P(B)>0, BIS
P(A|B)=P(A B)/P(B) (AIS).
Tak więc P(A B)=P(A|B)P(B) (także P(A B)=P(B|A)P(A), jeżeli P(A)>0)
Wzór na prawdopodobieństwo całkowite, wzór Bayesa:
Jeżeli Aj IS (i=1,2,,n) są parami rozłączne, P(Ai)>0 i A1 A2 An=E oraz BIS, to
P(B)=P(B|A1)P(A1)+ P(B|A2)P(A2)++ P(B|An)P(An).
Ponadto wtedy
P(Ak|B)=P(B|Ak)P(Ak)/P(B),
gdzie P(B) jest dane poprzednim wzorem.
Zmienne losowe.
Niech X:E R lub X:E R (tzw. rozszerzona funkcja rzeczywista, tzn. mogąca przyjmować także wartości oraz + ). Mówimy, że funkcja X jest zmienną losową, jeżeli
(i) Dla każdego przedziału P, zbiór jest zdarzeniem losowym, czyli należy do rodziny S; w szczególności, jest określone prawdopodobieństwo tego zbioru, tzn. prawdopodobieństwo, że zmienna losowa przyjmie wartość z przedziału P : P(), oznaczane w skrócie przez P(XIP
(ii) P()=P()=0
Będziemy zajmować się tylko zmiennymi losowymi dwóch następujących typów (choć istnieją zmienne, które nie są żadnego z tych typów):
a) typu skokowego: zmienna, przyjmująca skończoną lub przeliczalną ilość wartości, powiedzmy xi z prawdopodobieństwami odpowiednio pi (suma wszystkich pi jest równa 1);
b) typu ciągłego: zmienna, dla której
istnieje tzw. funkcja gęstości (krótko: gęstość) f, tzn. funkcja taka, że 1) f 0; 2) dla dowolnych a,
b, P(a X b)=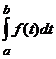 . Na to, aby funkcja f była gęstością pewnej zmiennej losowej X potrzeba i
wystarcza, aby f była nieujemna i
. Na to, aby funkcja f była gęstością pewnej zmiennej losowej X potrzeba i
wystarcza, aby f była nieujemna i 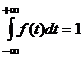 .
.
Dystrybuanta zmiennej losowej jest to funkcja F:( R, określona przez warunek F(x)=P(X<x)=P(). (Każda zmienna losowa ma dystrybuantę; nie każda zmienna losowa ma gęstość - tylko zmienna losowa typu ciągłego ma gęstość.)
Dla zmiennej X typu skokowego, F(x) jest równe sumie tych prawdopodobieństw pi, dla których odpowiednie xi spełniają warunek xi<x. Jeżeli zmienna losowa przyjmuje skończoną ilość wartości (lub nieskończoną ilość, ale odizolowanych od siebie wartości), to jej dystrybuanta jest funkcją schodkową.
Dla
zmiennej losowej X typu ciągłego o gęstości f mamy F(x)= 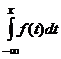 . Wtedy F jest ciągła, ponadto F(x)=f(x) w
punktach ciągłości funkcji f (więcej, nawet prawie
wszędzie, tzn. wszędzie z wyjątkiem być może pewnego
zbioru miary zero). Ponadto, wtedy P(X=x)=0 dla każdego x, tak że
wszystkie prawdopodobieństwa
. Wtedy F jest ciągła, ponadto F(x)=f(x) w
punktach ciągłości funkcji f (więcej, nawet prawie
wszędzie, tzn. wszędzie z wyjątkiem być może pewnego
zbioru miary zero). Ponadto, wtedy P(X=x)=0 dla każdego x, tak że
wszystkie prawdopodobieństwa
P(a X<b), P(a X b), P(a<X<b), P(a<X b)
są sobie równe (i równe całce 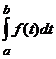 ).
).
Własności dystrybuanty dowolnej zmiennej losowej X:
0 F(x) (jako prawdopodobieństwo);
F - niemalejąca (oczywiste - zob. własność 9 prawdopodobieństwa);
jeżeli x dąży do minus nieskończoności, to F(x) dąży do 0;
jeżeli x dąży do plus nieskończoności, to F(x) dąży do 1;
F jest lewostronnie ciągła (wynika z własności 6) prawdopodobieństwa).
Wyrażenie prawdopodobieństw przyjmowania wartości z pewnego przedziału przez zmienną losową za pomocą dystrybuanty:
P(a X<b)=F(b)F(a) P(a X b)=F(b+)F(a)
P(a<X<b)=F(b)F(a+) P(a<X b)=F(b+)F(a+)
W szczególności
P(X<a)=F(a), zgodnie z definicją dystrybuanty; P(X a)=F(a+);
P(X a)=1F(a); P(X a)=1F(a+).
Najważniejsze rozkłady prawdopodobieństwa zmiennych losowych.
1) Rozkład dwupunktowy: P(X=1)=p (0<p<1); P(X=0)=q=1p
2) Rozkład dwumianowy, czyli rozkład Bernoulliego:
![]()
[ta definicja jest poprawna, gdyż 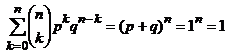 ].
].
Rozkład dwupunktowy jest oczywiście szczególnym przypadkiem rozkładu Bernoulliego, z n=2. Ilość sukcesów w n niezależnych eksperymentach, jeżeli prawdopodobieństwo sukcesu w pojedynczym eksperymencie jest równe p , ma rozkład Bernoulliego. Zmienną losową o rozkładzie Bernoulliego można traktować jako sumę n niezależnych zmiennych losowych o rozkładzie dwupunktowym: X=X1+X2+ +Xn (wynika to z prostego faktu, że suma wyrazów ciągu, składającego się z samych zer i jedynek, jest równa właśnie ilości jedynek w tym ciągu.
3) Rozkład Poissona: ![]() .
.
Rozkład Poissona jest granicznym przypadkiem rozkładu dwumianowego: gdy Xn mają rozkład dwumianowy o parametrach n, pn odpowiednio, n dąży do nieskończoności, a prawdopodobieństwa pn dążą do zera w ten sposób, że npn dąży do l, to prawdopodobieństwa P(Xn=k) przy dowolnym k dążą do odpowiednich prawdopodobieństw w rozkładzie Poissona. Rozkład Poissona jest stablicowany.
4) Rozkład normalny (Gaussa). Jest to rozkład typu ciągłego o gęstości
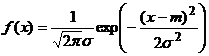
gdzie m (dowolne) i s>0 są ustalonymi parametrami (ich sens zostanie wyjaśniony później - okaże się wtedy, że m jest wartością oczekiwaną, zaś s - odchyleniem standardowym tej zmiennej). To, że podana funkcja jest rzeczywiście gęstością, wynika z podstawowej całki
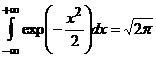 .
.
Jeżeli zmienna
losowa X ma rozkład normalny o parametrach (m,s), to piszemy X~N(m,s). Jeżeli X~N(m,s), to zmienna ![]() ma rozkład
N(0,1), który jest stablicowany. Istnieją tablice gęstości
(których używać będziemy rzadziej) oraz najważniejsze -
które występują w dwóch wariantach: albo są to bezpośrednio
tablice dystrybuanty F rozkładu normalnego N(0,1) - charakteryzują
się tym, że F(0)=0,5 (np. tablice w skrypcie Eugenii Ciborowskiej -
Wojdygi), albo też tablice pomocniczej funkcji
ma rozkład
N(0,1), który jest stablicowany. Istnieją tablice gęstości
(których używać będziemy rzadziej) oraz najważniejsze -
które występują w dwóch wariantach: albo są to bezpośrednio
tablice dystrybuanty F rozkładu normalnego N(0,1) - charakteryzują
się tym, że F(0)=0,5 (np. tablice w skrypcie Eugenii Ciborowskiej -
Wojdygi), albo też tablice pomocniczej funkcji
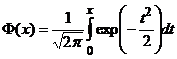
(te tablice charakteryzują się tym, że F(0)=0; mamy F(x)=F(x), F(x)=0,5+F(x); dla x<0 stosujemy F(x)=0,5F(|x|)).
Funkcje zmiennych losowych.
Jeżeli X jest zmienną losową i jeżeli g:R R jest funkcją taką, że g(X) jest również zmienną losową (jest tak na przykład, gdy g jest funkcją monotoniczną lub ciągłą, lub - jeszcze ogólniej, tzw. funkcją Bairea, tj. taką, że dla dowolnego przedziału postaci ( ,a) jego przeciwobraz przy odwzorowaniu g jest również zbiorem borelowskim). Wtedy rozkład zmiennej Y=g(X) możemy znaleźć w sposób następujący:
1) Jeżeli X jest zmienną typu skokowego, przyjmującą wartości xi z prawdopodobieństwami odpowiednio pi , to Y jest również zmienną typu skokowego, przyjmującą wartości yi =g(xi) z prawdopodobieństwami qi , gdzie qi jest równe sumie tych wszystkich pj , że g(xj)=yi. (może się bowiem zdarzyć, że dla różnych xj ich obrazy przy g są takie same.)
2) Dystrybuantę FY zmiennej losowej Y=g(X) możemy zawsze wyznaczyć poprzez dystrybuantę FX zmiennej losowej X: mamy FY(y)=P(Y<y)=P(g(X)<y), a dalszy proces obliczania FY zależy od tego, jaką postać ma rozwiązanie nierówności g(X)<y względem X - musimy P(g(X)<y) wyrazić w postaci P(XIAy), gdzie Ay jest pewnym zbiorem zależnym od y; jeżeli jest to suma przedziałów, możemy to prawdopodobieństwo wyrazić za pomocą dystrybuanty FX zmiennej X.
3) Jeżeli X jest typu ciągłego o gęstości fX, to związek pomiędzy gęstościami fY i fX otrzymujemy poprzez różniczkowanie odpowiedniego związku pomiędzy dystrybuantami. Istnieje pewien wzór na zależność pomiędzy gęstościami, ale niestety ważny tylko w przypadku, gdy g jest monotoniczna. Ogólnie rzecz biorąc, musimy rozpatrywać różne przypadki w zależności od postaci rozwiązania wspomnianych wyżej nierówności.
Zmienne losowe wielowymiarowe.
Niech (X,Y) będzie dwuwymiarową zmienną losową. Dla zmiennych typu skokowego, rozkład jest wyznaczony przez podanie liczb pij=P(X=xi,Y=yj). Dla zmiennych typu ciągłego istnieje gęstość, tzn. funkcja nieujemna f taka, że dla dowolnych a<b, c<d
P(a X b, c Y d)=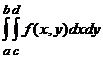 . Oczywiście,
. Oczywiście, 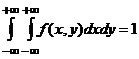 .
.
Dla dwuwymiarowej zmiennej losowej możemy zawsze wprowadzić dystrybuantę F(x,y)=P(X<x,Y<y). Tak więc np.
P(a X<b, c Y<d)=F(b,d)F(b,c)F(a,d)+F(a,c).
Podanie rozkładu dwuwymiarowego zmiennej (X,Y) określa, w szczególności, rozkłady samych zmiennych X i Y - czyli tzw. rozkłady brzegowe. Dla zmiennych typu skokowego rozkład X jest wyznaczony przez liczby pi Sj pij , zaś rozkład zmiennej Y jest wyznaczony przez liczby p j Si pij .
Mamy wtedy również FX(x)=F(X,Y)(x,+ ), FY(y)==F(X,Y)(+ ,y).
Dla zmiennych typu
ciągłego, rozkład (brzegowy) zmiennej X jest wyznaczony przez
gęstość 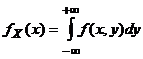 i analogicznie,
rozkład (brzegowy) zmiennej Y przez jej gęstość
i analogicznie,
rozkład (brzegowy) zmiennej Y przez jej gęstość 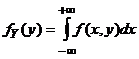 .
.
Mówimy, że zmienne losowe X i Y są niezależne, jeżeli dla dowolnych przedziałów P P zachodzi P(XIP ,YIP )=P(XIP ) P(YIP ). Jest to równoważne temu, że
F(X,Y)(x,y)=FX(x)FY(y) dla dowolnych x, y.
Dla zmiennych typu ciągłego mamy następny równoważny warunek: f(X,Y)(x,y)=fX(x)fY(y) dla dowolnych x, y.
Wartość oczekiwana i inne parametry zmiennej losowej
Wartością oczekiwaną (lub wartością średnią) zmiennej losowej X nazywamy:
1) w przypadku zmiennej losowej typu skokowego, przyjmującej wartości xi z prawdopodobieństwami odpowiednio pi - liczbę
![]()
2) w przypadku zmiennej losowej typu ciągłego o gęstości f - liczbę
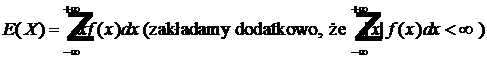
Definicje te możemy uogólnić na przypadek, gdy dana jest pewna funkcja g zmiennej losowej X, i w konsekwencji mamy do czynienia z nową zmienną losową Y=g(X). Jeżeli chcemy obliczyć jej wartość oczekiwaną E(Y)=E(g(X)), to z definicji musielibyśmy policzyć najpierw rozkład (tzn. odpowiednie wartości yi oraz ich prawdopodobieństwa qi dla zmiennej Y=g(X) albo też odpowiednią gęstość fY zmiennej losowej Y) a następnie zastosować odpowiedni z powyższych wzorów. Okazuje się jednak, że wartość oczekiwaną zmiennej g(X) możemy też obliczyć bezpośrednio, a mianowicie:
1) w przypadku zmiennej losowej typu skokowego, przyjmującej wartości xi z prawdopodobieństwami odpowiednio pi -mamy
![]()
2) w przypadku zmiennej losowej typu ciągłego o gęstości f - mamy

W szczególności, możemy określić tzw. momenty (zwykłe) wyższych rzędów (rzędu k):
1) w przypadku zmiennej losowej typu skokowego, przyjmującej wartości xi z prawdopodobieństwami odpowiednio pi - mamy
![]()
2) w przypadku zmiennej losowej typu ciągłego o gęstości f - mamy
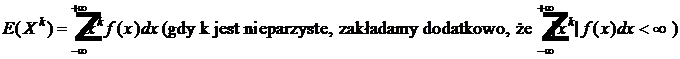
Co więcej, wzory na E(g(X)) uogólniają się nawet na przypadek funkcji dwóch lub więcej zmiennych losowych, np.
1) gdy (X,Y) jest dwuwymiarową zmienną losową typu skokowego, pij=P(X=xi,Y=yj), to
![]()
2) gdy (X,Y) jest dwuwymiarową zmienną losową typu ciągłego o gęstości f(x,y), to

Własności wartości oczekiwanej zmiennej losowej:
E(X+Y)=E(X)+E(Y);
E(aX)=aE(X).
Jeżeli zmienne losowe X i Y są niezależne, to E(XY)=EX EY.
Wariancja i odchylenie standardowe zmiennej losowej
Niech X będzie zmienną losową, przy czym zakładamy, że istnieje jej wartość oczekiwana m=EX. Przez wariancję zmiennej losowej X rozumiemy liczbę, oznaczaną przez D2X, WX lub VX, mianowicie
D2X=WX=VX=E[(Xm)2].
Tak więc, mamy
![]() względnie
względnie 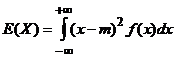
odpowiednio dla zmiennej losowej typu skokowego oraz ciągłego. Proste przeliczenie daje wzór WX = E(X2)(EX)2 . Odchyleniem standardowym zmiennej losowej X, oznaczanym przez s(X), nazywamy pierwiastek kwadratowy z wariancji zmiennej X.
Własności wariancji:
W(aX)=|a|2WX;
W(X+Y)=WX+WY+2(E(XY)(EX)(EY));
w szczególności, jeżeli X i Y są niezależne, to W(X+Y)=WX+WY.
Analogicznie do wariancji, możemy określić tzw. moment centralny rzędu k jako
mk(X) = E[(Xm)k], gdzie m=EX jak poprzednio.
Parametry podstawowych rozkładów.
|
Rozkład X |
EX |
E(X2) |
WX |
|
dwupunktowy |
p |
p |
pq |
|
Bernoulliego o parametrach (n,p,q=1p) (czyli dwumianowy) |
np |
n(n1)p2+np |
npq |
|
Poissona z parametrem l |
l |
l |
l |
|
normalny (Gaussa) tzn. N(m,s |
m |
s |
Centralne twierdzenie graniczne (Lindenberga-Levyego).
Niech X1,X2, - będzie ciągiem niezależnych zmiennych losowych o jednakowym rozkładzie, posiadającym wartość oczekiwaną m i odchylenie standardowe s. Niech
Niech
![]() ;
;
Yn jest więc
normalizacją sumy X1+X2++Xn, przez
odjęcie od niej jej wartości oczekiwanej (tzn. nm) i podzielenie jej przez jej odchylenie standardowe (tzn. ![]() ), co zapewnia, że E(Yn)=0, s(Yn)=1;
ostatnią postać otrzymujemy z kolei, dzieląc licznik i mianownik
przez n.
), co zapewnia, że E(Yn)=0, s(Yn)=1;
ostatnią postać otrzymujemy z kolei, dzieląc licznik i mianownik
przez n.
Wtedy rozkład zmiennej Yn dąży przy n do rozkładu normalnego N(0,1) w tym sensie, że jego dystrybuanta dąży (punktowo) do dystrybuanty FN(0,1) rozkładu normalnego N(0,1), tzn.
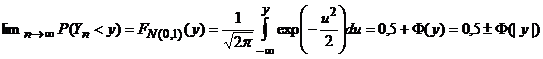
(+ gdy y 0; gdy y<0). Oznacza to, że dla dużych n zmienna losowa Yn ma w przybliżeniu rozkład normalny N(0,1). W praktyce przyjmujemy, że przybliżenie to jest wystarczająco dobre dla n
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1411
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved