| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
| Будівництво | Електронний | Медицина | Освіта | Фінанси | географія | економіка | законодавство |
| косметика | маркетинг | математика | політика | право | психологія | різний | соціологія |
| техніка | управління | фізичний | харчування | інформацію | історія |
DOCUMENTE SIMILARE |
|
Роздільний
облік витрат
у
багатопродуктовому
виробництві
є складним,
неоднозначним
і може бути
здійснений
різними
способами.
Нижче пропонується
один із них.
Нехай ![]() обсяг
випущеної
продукції
обсяг
випущеної
продукції ![]() го виду
го виду ![]() загальні
витрати. На
основі
статистичної
інформації
про значення
цих величин у
відповідні
дискретні
моменти часу
можна
побудувати
рівняння
множинної регресії
загальні
витрати. На
основі
статистичної
інформації
про значення
цих величин у
відповідні
дискретні
моменти часу
можна
побудувати
рівняння
множинної регресії
![]() (20.1)
(20.1)
та
визначити
загальні
постійні витрати
![]() та
питомі
змінні витрати
та
питомі
змінні витрати
![]() Однак
проблема
розподілу
постійних витрат
за видами
продукції
залишається
відкритою.
Одним із
найпростіших
підходів до
її розв'язання
в нашій
ситуації є
розподіл
сумарних
постійних витрат
Однак
проблема
розподілу
постійних витрат
за видами
продукції
залишається
відкритою.
Одним із
найпростіших
підходів до
її розв'язання
в нашій
ситуації є
розподіл
сумарних
постійних витрат
![]() пропорційно
до змінних витрат,
тобто вважати,
що
пропорційно
до змінних витрат,
тобто вважати,
що
![]() (20.2)
(20.2)
де
![]()
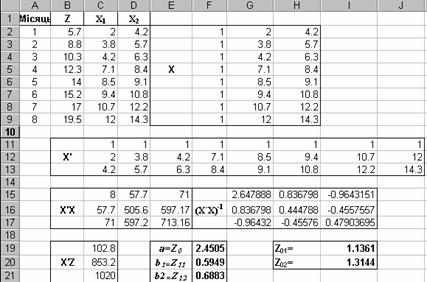
Нехай за 8
місяців
роботи в
системі
бухгалтерського
обліку
двопродуктового
виробництва
зафіксовані
величини
загальних витрат
![]() та
обсягів
випущеної
продукції
та
обсягів
випущеної
продукції ![]() і
і ![]() .
Побудувати
рівняння
множинної
регресії (20.1) і,
скориставшись
параметрами
регресії, визначити
постійні
.
Побудувати
рівняння
множинної
регресії (20.1) і,
скориставшись
параметрами
регресії, визначити
постійні ![]() та
питомі змінні
та
питомі змінні ![]()
На
підставі 8ми
місяців
роботи,
використовуючи
МНК і пакет Excel,
побудуємо
економетричну
модель для
функції (20.1). Щоб
знайти
параметри
моделі,
необхідно розрахувати
вектор 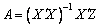 , де
, де ![]() транспонована
матриця,
транспонована
матриця, ![]() матриця,
обернена до
матриця,
обернена до ![]() .
.
1 дія
транспонування
матриці ![]() (функція
ТРАНСП);
(функція
ТРАНСП);
2 дія
множення
матриць ![]() та
та ![]() (функція
МУМНОЖ);
(функція
МУМНОЖ);
3 дія
знаходження
оберненої
матриці до
матриці ![]() (функція
МОБР);
(функція
МОБР);
4 дія
множення
матриці ![]() та
вектора
та
вектора ![]() (функція
МУМНОЖ);
(функція
МУМНОЖ);
5 дія
знаходження
параметрів
моделі ![]() ,
множенням
матриць
,
множенням
матриць ![]() та
та ![]() .
.
Зазначимо,
що у випадку
двопродуктової
моделі
співвідношення
(20.2) має такий
вигляд: ![]() =
=![]() , де
, де ![]()
Ctrl Shift Enter
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2096
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved