Corelari ale diferentelor de faza - GPS

Corelari ale diferentelor de faza - GPS

In general, exista doua grupe de corelari: corelari fizice si corelari matematice.

Masuratorile de faza intre un satelit GPS "j" si doua receptoare GPS, amplasate in doua puncte A si B, in care se fac masuratori, (F^j_A (t) , F^j_B (t) se pot corela fizic foarte usor, atunci cand observatiile inregistrate se refera la acelasi satelit GPS.

Cum este si normal, consideram corelarile matematice, operatiile matematice care se fac cu grupul de masuratori si anume, cele induse de diferentele intre observatii.

Se accepta ca erorile masuratorilor de faza, urmeaza o distributie normala a mediei F si a variantei s . Masuratorile brute, de faze, sunt linear independente sau necorelate.

Daca definim un vector F care sa contina masuratorile de faze, putem scrie:

Cov (F) = s²I (1.56)

relatie care reprezinta matricea de varianta-covarianta pentru faze si I ,reprezinta,matricea unitate.

1 Diferente simple

Pornind de la ipoteza anterioara, pentru cele doua receptoare amplasate in punctele A si B, privitor la satelitii j si k, se pot scrie pentru epoca t cate o ecuatie de diferenta simpla pentru fiecare satelit, conform relatiei (1.40).

Daca aceste relatii sunt scrise sub forma matriciala, se obtine:

SD = C F (1.57)

unde termenii formulei reprezinta:

(1.58)

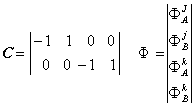(1.59)

Aplicand legile de propagare a covariantei in relatia (1.57), se obtine:

cov (SD) = C cov (F) C^T   

si prin inlocuire in (1.56), rezulta:

cov (SD) = C s I C^T s C C^T    (1.61)

(1.62)

Inlocuind relatia (1.61) se obtine matricea de varianta-covarianta pentru diferenta simpla:

cov (SD) = 2 s I

Rezulta ca, diferentele simple, sunt necorelate. Dimensiunea matricei unitare corespunde numarului de simple diferente la epoca t , factorul 2 din relatie neavand legatura cu numarul de diferente simple. Considerand inca o epoca de masuratori, matricea de varianta-covarianta este tot o matrice unitara ale carei dimensiuni sunt date de numarul intreg de diferente simple.

2 Diferente duble

Considerand aceleasi puncte A si B, in care se fac inregistrari de catre doua receptoare, asupra a trei sateliti j, k si l dintre care, satelitul j va fi considerat satelit de referita.

Daca se are in vedere doar epoca t rezulta urmatoarele ecuatii specifice diferentelor duble:

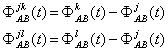(1.64)

Aceste ecuatii se pot scrie sub forma matriciala:

DD =C SD

in care termenii, au urmatoarele expresii:

(1.66)

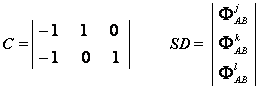(1.67)

Matricea de varianta-covarianta pentru dubla diferenta de faze, este data de relatia:

cov (DD) = C cov (SD) C^T (1.68)

si daca se inlocuieste cu expresia din relatia (1.63), obtinem:

cov (DD) = 2 s C C^T

Inlocuindu-se valoarea lui C din relatia (1.67) se obtine:

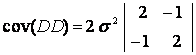(1.70)

Dupa cum se poate observa, in cazul dublei diferente rezultatele sunt corelate.

Matricea ponderilor P (t), se obtine din inversa matricei de varianta-covarianta:

P (t)=[cov (DD)]^-1 (1.71)

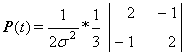(1.72)

unde doua duble diferente sunt utilizate la aceeasi epoca t.

Daca, cu n_DD , se noteaza numarul de diferente duble la epoca t, matricea de corelatie este data de relatia:

(1.73)

Pana la acest moment demonstratia s-a axat pe masuratorile efectuate intr-o singura epoca, t. In conditii normale numarul de epoci este foarte mare si in acest caz, matricea de corelare este o matrice bloc-diagonala cu dimensiunea n_i , unde i =1,2,...n:

(1.74)

unde fiecare element al acestei matrici, este o matrice asemanatoare, pentru fiecare epoca de masurare.

3 Diferente triple

Ecuatiile pentru diferentele triple sunt ceva mai complicate, deorece trebuie considerata fiecare situatie. Covarianta unei singure triple diferente este dedusa prin aplicarea regulii de propagare a covariantei, prezentata in relatiile (1.49).

Considerand ipoteza de la diferenta dubla,cu satelitul j considerat satelit de referinta, dar la doua epoci de masurare, t₁ si t₂ , rezulta:

(1.75)

Aceste doua ecuatii pot fi scrise sub forma matriciala, dupa cum urmeaza:

TD = C SD (1.76)

relatie in care termenii au urmatoarea semnificatie:

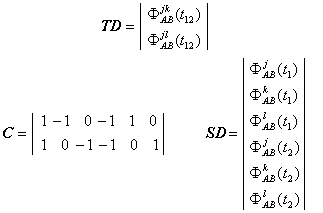(1.77)

Matricea de covarianta pentru diferenta tripla, are urmatoarea forma:

cov (TD) = C cov (SD) C^T (1.78)

in care daca se substituie relatia (1.63), se obtine:

cov (TD) = 2 s C C^T

Inlocuind si relatiile din (1.77) se obtine[Hofmann -Wellenhof, s.a.,1992]:

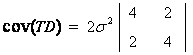(1.80)

Dupa cum se poate observa, in cazul diferentei triple rezultatele sunt corelate.

Matricea ponderilor P (t), se obtine din inversa matricei de varianta-covarianta prezentata in relatia (1.80).