| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Un sistem de comunicatii vehiculeaza un semnal purtator de informatie de la un emitator spre unul sau mai multi destinatari, folosind in acest scop un canal de comunicatii. Dezvoltarea deosebit de dinamica a comunicatiilor digitale se datoreaza urmatorilor factori:
q Convergenta tehnologiilor de telecomunicatii cu cele de calculatoare, calculatorul personal devenind si un terminal inteligent de telecomunicatii;
q Sistemele de comunicatii digitale asigura o deosebita flexibilitate transmisiei, ele putand transmite informatii de naturi diferite (convorbiri telefonice, muzica, imagini fixe si mobile, date) sub forma digitala si cu o calitate superioara;
q Proliferarea canalelor de banda larga (fibra optica, sateliti geostationari de telecomunicatii, linii in cablu coaxial);
q Perfectionarea tehnologiilor de fabricatie a circuitelor integrate, scaderea densitatii de integrare a componentelor impreuna cu cresterea complexitatii sistemelor si a vitezei de lucru cu 1-2 ordine de marime in ultima decada;
q Aparitia de noi tehnici si servicii de telecomunicatii (radiotelefonie celulara, transmisii de date de mare viteza, comunicatii Internet, posta electronica, videotelefonie, videoconferinta, videosupraveghere, transmisii de imagini, etc.).
Avantajele oferite de comunicatiile digitale sunt urmatoarele:
q Folosirea unor circuite (hard-ware) digitale relativ ieftine si a tehnicilor de procesare digitala a semnalelor conduce la sisteme cu performante crescute si cost scazut;
q Tehnologiile digitale pot creste capacitatea sistemului de 2 pana la 5 ori in comparatie cu cele analogice folosind tehnici de acces multiplu, codare si modulatie;
q Calitate superioara oferita de tehnicile digitale (distorsiuni reduse si fiabilitate crescuta);
q Asigurarea secretizarii mesajelor transmise utilizand tehnici digitale de criptare (cifrare);
q In sistemele de comunicatii digitale la mare distanta, spre deosebire de cele analogice, nu se cumuleaza distorsiunile si zgomotele de la repetor la repetor;
q Rata erorilor este suficient de mica, chiar in conditiile unor zgomote de putere mai mare ce afecteaza transmisia;
q Se pot elimina in mare masura erorile prin introducerea de redundanta (codare).
Ca dezavantaje ale comunicatiilor digitale putem considera:
q In general, sistemele de comunicatiile digitale necesita o banda mai mare in comparatie cu cele analogice;
q La receptie trebuie realizate operatii de sincronizare (de purtatoare, de bit, de cadru, de cuvint) ceea ce conduce la o complexitate crescuta a sistemului si in special a receptoarelor.
Canalele reale utilizate in comunicatiile digitale prezinta o serie de neajunsuri si imperfectiuni sau defecte, iar semnalele receptionate difera mult de cele transmise. Dintre defectele principale si transformarile suferite de semnal amintim:
q Distorsionarea semnalului datorita operatiilor de filtrare, translare de frecventa, modulare si demodulare;
q
Translarea spectrului semnalului cu o
frecventa variabila ![]() ,
produsa de miscarea relativa intre emitator si
receptor, cunoscuta ca efect Doppler;
,
produsa de miscarea relativa intre emitator si
receptor, cunoscuta ca efect Doppler;
q Propagare necontrolata, pe cai adiacente celei principale, cunoscuta si ca propagare multi-cai sau multipath.
q Zgomote de tip aditiv si multiplicativ, cu caracter aleator, care afecteaza amplitudinea, respectiv faza semnalului;
q Atenuarea aleatoare sau sub forma unei functii de timp care nu depinde de semnalul transmis, cunoscuta sub denumirea de fading;
q Interferente la intrarea sau iesirea din canal, produse de alte sisteme de comunicatii sau de fenomene naturale.
Interferenta produsa de semnalele din canalele alaturate, avand frecventa cea mai apropiata, se numeste interferenta canalului adiacent, pe scurt ACI (Adjacent Channel Interference). In general ea se datoreaza imperfectiunii filtrelor receptorului care aduc in banda de trecere o parte atenuata insuficient a energiei semnalelor din afara benzii. Ea este foarte importanta in comunicatiile mobile.
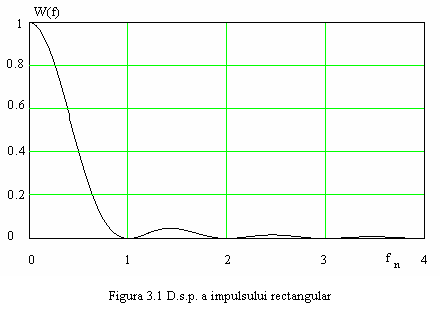 Impulsul
rectangular utilizat pentru transmisie are un spectru infinit. Semnalul de date
este transmis printr-un canal de comunicatie de banda limitata.
Ca urmare spectrul semnalului transmis este limitat si distorsionat.
Impulsul
rectangular utilizat pentru transmisie are un spectru infinit. Semnalul de date
este transmis printr-un canal de comunicatie de banda limitata.
Ca urmare spectrul semnalului transmis este limitat si distorsionat.
Canalul de banda finita va produce o rotunjire si alungire a impulsurilor care nu mai prezinta fronturi abrupte si se intind pe durata a mai multor intervale de simbol. In figura 3.1 este prezentat spectrul de putere al unui semnal de date rectangular.
In majoritatea sistemelor de telecomunicatii costurile sunt strans legate de banda utilizata.
 Limitarea
benzii cana-lului este echivalenta cu o filtrare trece-jos sau
trece-banda. Pe linia folosita pentru transmisie pot exista
transformatoare si condensatoare de cuplaj care determina un spectru
transmis cu componenta de c.c. nula si componente reduse de
joasa frecventa.
Limitarea
benzii cana-lului este echivalenta cu o filtrare trece-jos sau
trece-banda. Pe linia folosita pentru transmisie pot exista
transformatoare si condensatoare de cuplaj care determina un spectru
transmis cu componenta de c.c. nula si componente reduse de
joasa frecventa.
Considerente de multiplexare in frecventa sau separare a benzilor laterale pentru semnalele modulate pot dicta o filtrare trece-sus a semnalului ce urmeaza a fi transmis.
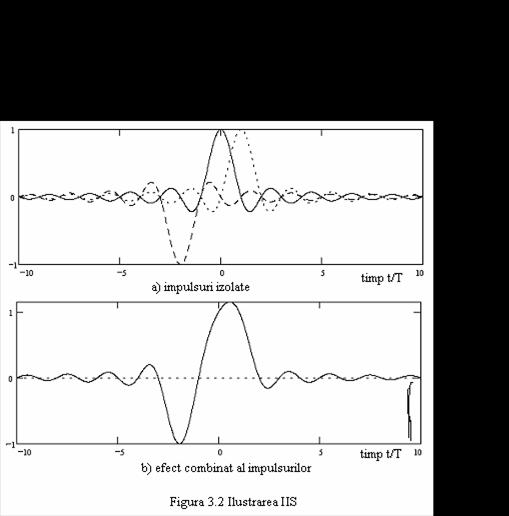
Efectul limitarii benzii se manifesta prin rotunjirea fronturilor si extinderea duratei impulsului de semnalizare pe durata a mai multor intervale de simbol. In consecinta, o parte din energia formei de unda utilizate pentru transmisie este redistribuita spre intervalele de simbol invecinate, iar impulsurile transmise se vor suprapune partial in cel mai bun caz sau in mare masura in cazul limitarii severe a benzii. Acest fenomen este cunoscut ca interferenta intersimboluri (IIS).
Un exemplu de IIS se poate observa in figura 3.2 in cazul unei transmisii ternare, considerand o secventa de date de tipul .0,0,-1, 0, +1, +1, 0, 0, .
Recuperarea informatiei transmise are loc la receptie in multe cazuri prin esantioanrea semnalului receptionat la anumite momente de timp urmat de compararea valorii esantioanelor cu o valoare de referinta. In cazul prezentei IIS valoarea esantionului va depinde atat de forma de unda transmisa pe intervalul de timp propriu cat si de contributiile formelor de unda transmise pe intervalele de simbol alaturate.
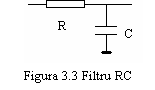 Examplul
I Sa consideram un filtru RC simplu reprezentat in figura 3.3.
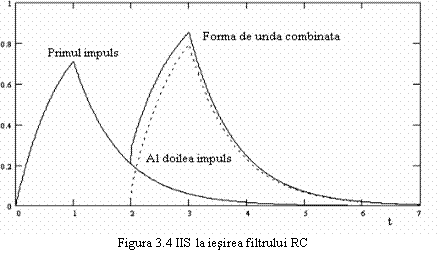
Fronturile impulsului rectangular sunt rotunjite si apar sub forma unor
exponentiale. O parte din energia impulsului difuzeaza in intervalele
de bit alaturate si se combina aditiv cu impulsurile
urmatoare, ca urmare crescand amplitudinea semnalului transmis. Un caz
particular este ilustrat in figura 3.4.
Examplul
I Sa consideram un filtru RC simplu reprezentat in figura 3.3.
Fronturile impulsului rectangular sunt rotunjite si apar sub forma unor
exponentiale. O parte din energia impulsului difuzeaza in intervalele
de bit alaturate si se combina aditiv cu impulsurile
urmatoare, ca urmare crescand amplitudinea semnalului transmis. Un caz
particular este ilustrat in figura 3.4.
In cazul filtrarii trece sus a semnalului rezulta un impuls fara componenta de c.c. iar in locul mentinerii palierului va apare o comportare descrescatoare. Impulsul este alungit dar coada sa se combina subtractiv cu impulsurile invecinate, micsorand energia semnalului transmis in unele cazuri si corespunzator amplitudinea.
Din punct de vedere practic IIS se limiteaza la 3-5 intervale de bit, desi teoretic ea se intinde pe durate mult mai mari. Daca FTJ echivalent prezinta o caracteristica de faza neliniara, vor apare distorsiuni de faza care distrug simetria para de amplitudine a impulsului si a cozilor sale iar deformarea este mai puternica.

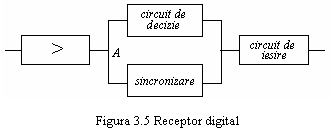 Efectul
IIS, al distorsiunilor de faza si amplificare precum si al
zgomotului este de obicei studiat pentru
partea din sistemul de transmisie reprezentat in figura 3.5 prin vizualizarea
formei de unda din punctul A. Se
poate proceda in doua moduri:
Efectul
IIS, al distorsiunilor de faza si amplificare precum si al
zgomotului este de obicei studiat pentru
partea din sistemul de transmisie reprezentat in figura 3.5 prin vizualizarea
formei de unda din punctul A. Se
poate proceda in doua moduri:
Vizualizand intreaga secventa de date transmisa pe un anumit interval de timp (durata caracterului sau cadrului), asa cum se observa in figura 3.6;
2. Sincronizand baza de timp a oscilatorului cu
frecventa de bit sau simbol si vizualizand un interval de bit sau
simbol.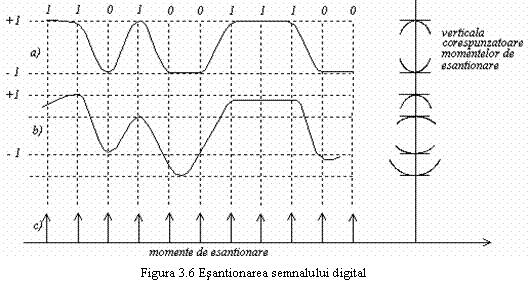

 In cazul
2 se obtine un efect de suprapunere a tuturor formelor de unda din
intervalele alaturate si o reprezentare condensata a starilor
semnalului si a tranzitiilor intre stari. Figura astfel obtinuta
pe ecranul osciloscopului, pentru o TD binara, se numeste diagrama
ochiului, datorita formei sale specifice, reprezentata in partea
dreapta a figurii 3.6. Se observa din figura 3.6 ca, datorita
IIS si zgomotelor, ochiul nu mai este complet deschis la momentele de
esantionare (cazul a) ci devine partial inchis.
In cazul
2 se obtine un efect de suprapunere a tuturor formelor de unda din
intervalele alaturate si o reprezentare condensata a starilor
semnalului si a tranzitiilor intre stari. Figura astfel obtinuta
pe ecranul osciloscopului, pentru o TD binara, se numeste diagrama
ochiului, datorita formei sale specifice, reprezentata in partea
dreapta a figurii 3.6. Se observa din figura 3.6 ca, datorita
IIS si zgomotelor, ochiul nu mai este complet deschis la momentele de
esantionare (cazul a) ci devine partial inchis.
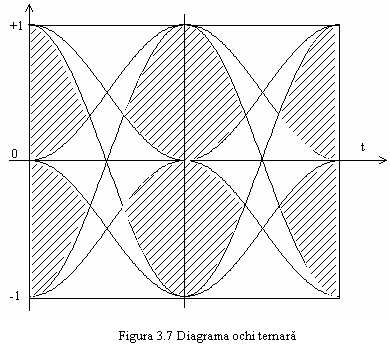
In figura 3.7 este reprezentata diagrama ochiului (D.O.) pentru o transmisie ternara cu nivelele 1 si 0, fara IIS si zgomot, in diagrama ochiului aparand toate tranzitiile posibile, fiecare curba fiind afectata doar de cele doua valori ternare vecine.
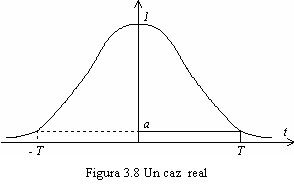 In cazul
real, impulsurile transmise prezinta o trena cu valori oscilante,
care produce IIS; ele nu mai trec prin zero la mijlocul intervalelor Nyquist,
situatie reprezentata de in figura 3.8.
In cazul
real, impulsurile transmise prezinta o trena cu valori oscilante,
care produce IIS; ele nu mai trec prin zero la mijlocul intervalelor Nyquist,
situatie reprezentata de in figura 3.8.
Deschiderea ochiului pe verticala se noteaza cu E si depinde de numarul de nivele al codului folosit. Daca impulsul tip cosinus ridicat se distorsioneaza si ia valorile a la momentele -T si T, deschiderea ochiului va fi:
![]() (3.1)
(3.1)
unde L - numarul de nivele ale codului utilizat in transmisie.
 IIS,
reprezentata de termenul al doilea dinmembrul doi al relatiei (3.1)
este data de:
IIS,
reprezentata de termenul al doilea dinmembrul doi al relatiei (3.1)
este data de:
![]() (3.2)
(3.2)
iar fata de cazul ideal,
deschiderea ochiului se reduce cu ![]() . o
anumita probabilitate de eroare, raportul
. o
anumita probabilitate de eroare, raportul ![]() trebuie crescut cu
trebuie crescut cu ![]() fata de cazul ideal.
fata de cazul ideal.
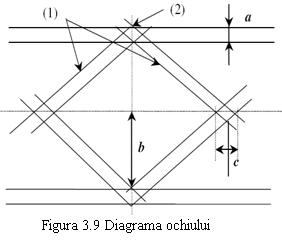
Deschiderea ochiului E reprezinta diferenta minima garantata dintre valorile nivelelor codului, pentru care se poate lua decizia. Rezulta deci, pentru o TD reala, cu IIS si zgomote, ca pentru a garanta o anumota probabilitate de eroare, raportul S/Z trebuie crescut cu 1/E fata de cazul ideal. Diagrama schematizata a ochiului este reprezentata in figura 3.9, pe baza ei putand obtine o serie de indici calitativi privind performanta unui sistem de TD:
. momentele optime de esantionare: verticala corespunzatoare deschiderii maxime a ochiului (1);
. sensibilitatea sistemului la momentele de esantionare - data de pantele curbelor care marcheaza inchiderea ochiului;
. distorsiunea maxima a semnalului - data de latimea a a celor doua ramuri ale ochiului pe verticala momentului de esationare;
. marginea de zgomot - data de distanta b de la pragul de decizie la cea mai apropiata valoare esantionata;
. distorsiunea trecerii prin zero - data de latimea c a diagramei ochiului corespunzatoare momentului trecerii prin zero, utilizata atunci cand trecerile prin zero sunt folosite pentru sincronizarea
tactului.
Efectul Doppler a fost descoperit in secolul XIX de fizicianul austriac Christian Doppler si de francezul Fizeau si e cunoscut ca efect Doppler-Fizeau. Se spune ca a fost observat pentru prima data atunci cand locomotivele de pe calea ferata emiteau un fluierat. La apropierea trenului sunetul era mai inalt iar la departarea trenului sunetul devenea mai grav.
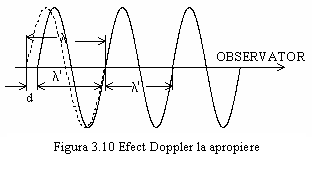 El apare
atunci cand intre sursa si observator exista o miscare
relativa. Sa consideram situatia reprezentata in
figura 3.10, cand sursa se apropie fata de observator. Ca urmare,
lungimea de unda a semnalului emis
El apare
atunci cand intre sursa si observator exista o miscare
relativa. Sa consideram situatia reprezentata in
figura 3.10, cand sursa se apropie fata de observator. Ca urmare,
lungimea de unda a semnalului emis ![]() ,
tinand cont de aceasta apropiere, devine aparent mai
mica
,
tinand cont de aceasta apropiere, devine aparent mai
mica ![]() Sa notam cu
Sa notam cu
 c viteza de propagare a undelor emise
c viteza de propagare a undelor emise
v - viteza sursei fata de observator.
Atunci, modificarea lungimii de unda ![]() , este
data de
, este
data de
![]() (3.3)
(3.3)
iar ![]() (3.4)
(3.4)
Frecventa modificata ![]() ce corespunde lui
ce corespunde lui ![]() este data de
este data de
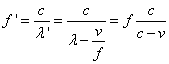 (3.5)
(3.5)
tinand cont ca ![]()
Daca sursa se departeaza de observator, frecventa modificata este data de
![]() (3.6)
(3.6)
Ca urmare a efectului Doppler, intre emitator si receptor apare o diferenta de frecventa
![]() (3.7)
(3.7)
 iar
componentele spectrale ale semnalului receptionat sunt translate cu
iar
componentele spectrale ale semnalului receptionat sunt translate cu ![]() . Acest
proces afecteaza detectia semnalului si introduce erori. Aceasta
se intelege usor presupunand ca la emisie frecventa de bit
si frecventa purtoare sunt legate armonic
. Acest
proces afecteaza detectia semnalului si introduce erori. Aceasta
se intelege usor presupunand ca la emisie frecventa de bit
si frecventa purtoare sunt legate armonic
![]() n
intreg (3.8)
n
intreg (3.8)
Evident,
![]() (3.9)
(3.9)
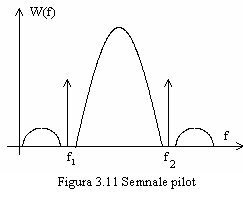
Pentru eliminarea
efectului Doppler se poate recurge la o tehnica de transmisie cu semnale
pilot, ilustrata in figura 3.11. Evident, cele doua semnale pe
frecventele ![]() si
si ![]() sunt afectate cu aceeasi cantitate
sunt afectate cu aceeasi cantitate ![]() , astfel
ca daca la emisie avem
, astfel
ca daca la emisie avem
![]() (3.10)
(3.10)
la receptie vom avea
![]() (3.11)
(3.11)
Pentru plasarea semnalelor pilot in spectrul semnalului transmis, trebuie create nuluri spectrale la frecvente adecvate, ceea ce se poate realiza printr-o codare de linie corespunzatoare sau utilizand tehnica semnalelor cu raspuns partial.
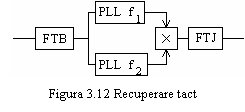
Recuperarea frecventei de tact ![]() neafectate de efectul Doppler se poate realiza
cu schema din figura 3.12. In locul FTJ sau dupa acesta se foloseste
un circuit PLL acordat pe frecventa de tact dorita.
neafectate de efectul Doppler se poate realiza
cu schema din figura 3.12. In locul FTJ sau dupa acesta se foloseste
un circuit PLL acordat pe frecventa de tact dorita.
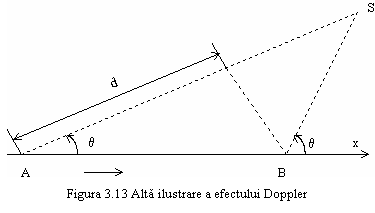
Daca miscarea sursei sau observatorului are loc pe o directie ce face un unghi cu linia ce uneste sursa cu observatorul, relatia de calcul a frecventei se schimba. Sa consideram situatia reprezentata in figura 3.13.
Considerand un mobil ce se misca din A spre B
cu o viteza ![]() pe o directie ce face unghiul
pe o directie ce face unghiul ![]() cu directia de propagare a undelor iar
sursa la o distanta suficient de mare pentru a putea considera
caile SA si SB paralele, diferenta de faza ce apare poate
fi scrisa ca
cu directia de propagare a undelor iar
sursa la o distanta suficient de mare pentru a putea considera
caile SA si SB paralele, diferenta de faza ce apare poate
fi scrisa ca
![]() (3.12)
(3.12)
iar frecventa instantanee sau deviatia de frecventa produsa prin efect Doppler este derivata fazei
![]() (3.13)
(3.13)
Propagarea multicai apare in cazul radiocomunicatiilor in unde scurte datorita reflexiilor semnalului in ionosfera si in unde ultrascurte, avand in vedere valoarea mica a lungimii de unda si difuzia troposferica. In cel mai simplu caz, fenomenul multipath se poate modela considerand o singura cale indirecta in afara celei directe. Semnalul rezultat poate fi scris ca
![]() (3.14)
(3.14)
Se defineste intarzierea diferentiala ![]() ca
ca
![]() (3.15)
(3.15)
si se presupune mai mica decat durata bitului T.
 In cazul
in care la receptie interfera mai multe semnale cu amplitudini
In cazul
in care la receptie interfera mai multe semnale cu amplitudini ![]() si
intarzieri
si
intarzieri ![]() diferite, poate aparea situatia ca
suma semnalelor sa fie foarte mica sau chiar zero, pe care o denumim
fading. Evident, in aceasta situatie nu se mai poate face
detectia semnalului, functionarea circuitelor de sincronizare este
afectata si se introduc erori.
diferite, poate aparea situatia ca
suma semnalelor sa fie foarte mica sau chiar zero, pe care o denumim
fading. Evident, in aceasta situatie nu se mai poate face
detectia semnalului, functionarea circuitelor de sincronizare este
afectata si se introduc erori.
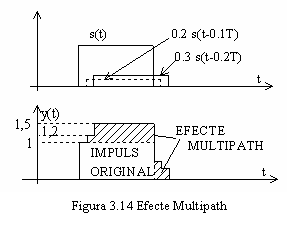
In figura 3.14 este ilustrat cazul cand avem 3
componente, cu amplitudinile 1, 0,2 si 0,3 si intarzierile 0, 0.1T
si 0,2T. Efectul de distorsionare al formei de unda
rectangulare, ce reprezinta informatia transmisa este clar
evidentiat. Se poate considera situatia aparuta si ca
un caz de interferenta intersimboluri, observand ca semnalele
intarziate vor afecta intervalul de bit urmator sau in cazuri grave,
intervalele de bit urmatoare. In functie de bitii succesivi
transmisi, energiile semnalelor inarziate se aduna aditiv sau
subtractiv cu energia de bit a semnalului pe intervalul considerat. De exemplu,
in cazul unei succesiuni ![]() ,
reprezentata ca
,
reprezentata ca ![]() ,
contributia semnalelor intarziate este pozitiva avand in vedere
ca ele corespund lui
,
contributia semnalelor intarziate este pozitiva avand in vedere
ca ele corespund lui ![]() , iar
bitul urmator corespunde lui
, iar
bitul urmator corespunde lui ![]() ,
adica o contributie de semn contrar. Aceste situatii vor
determina o crestere masiva a probabilitatii de eroare
si deci o scadere a calitatii transmisiei.
,
adica o contributie de semn contrar. Aceste situatii vor
determina o crestere masiva a probabilitatii de eroare
si deci o scadere a calitatii transmisiei.
Semnalele specifice TD sunt digitale (numerice) si
au caracter discret. In cel mai simplu caz datele pot fi considerate ca
simboluri matematice 0 si 1; in alte situatii se prefera
reprezentarea lor ca ![]()
Pentru realizarea TD, fiecarui simbol al sursei de date i se asociaza un fenomen fizic cunoscut care se propaga in canalul de comunicatii de la emitator spre receptor. Cazul cel mai raspandit utilizeaza propagarea undelor electromagnetice pe o linie sau in aer.
Unui simbol al sursei de date i se asociaza deci o
tensiune continua, o frecventa sau o faza a unei
oscilatii, care inerent sunt valori
discrete: ![]() .
Semnalul digital ia deci valori discrete:
.
Semnalul digital ia deci valori discrete: ![]() , pe
intervalele de timp discrete:
, pe
intervalele de timp discrete: ![]()
Valoarea discreta a semnalului este denumita stare semnificativa. Trecerea de la o stare semnificativa la urmatoarea se face in mod discontinuu si este denumita tranzitie (vezi figura 3.15).
Momentul in timp cand apare o tranzitie este denumit moment semnificativ. Doua momente semnificative succesive determina un interval semnificativ.
INTERVALUL ELEMENTAR (semnal elementar, impuls elementar, element de semnal) reprezinta cea mai scurta parte constitutiva a semnalului de date, deosebindu-se de celelalte prin amplitudine, durata si pozitie relativa.
In reprezentarea matematica informatia este
constituita din simbolurile binare![]() si
si
![]() . Secventa
de date se noteaza cu
. Secventa
de date se noteaza cu ![]() , unde
, unde ![]() este
simbolul de informatie transmis la momentul
este
simbolul de informatie transmis la momentul ![]() T fiind durata unui bit iar
T fiind durata unui bit iar ![]()
Pentru transmisie se prefera reprezentarea cu simboluri unipolare: 0, +1 sau bipolare: ![]() si
si ![]() .
Secventa de date codata bipolar se noteaza cu
.
Secventa de date codata bipolar se noteaza cu ![]() , cu
, cu ![]() .
Legatura dintre simbolurile
.
Legatura dintre simbolurile ![]() si
si ![]() este data de
este data de
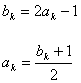 (3.16)
(3.16)
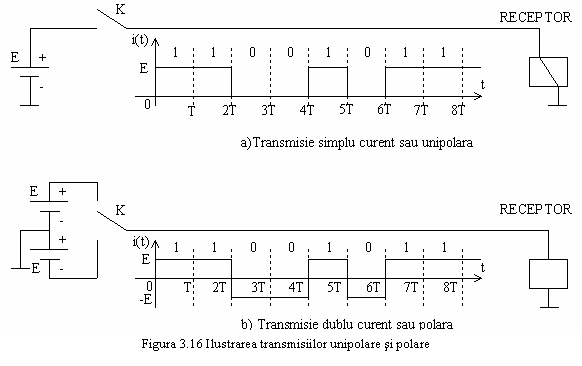
 Situatiile
corespunzatoare transmisiilor unipolare (simplu curent) si polare
(dublu curent) sunt reprezentate in figura 3.16.
Situatiile
corespunzatoare transmisiilor unipolare (simplu curent) si polare
(dublu curent) sunt reprezentate in figura 3.16.
In unele cazuri se prefera o transmisie ternara,
utilizand simbolurile ![]() .
Acestea pot reprezenta nivele de
tensiune, valori ale frecventei, fazei sau amplitudinii unui semnal.
Considerand simbolurile echiprobabile, puterea medie a semnalului digital in
cazul transmisiei binare bipolare este
.
Acestea pot reprezenta nivele de
tensiune, valori ale frecventei, fazei sau amplitudinii unui semnal.
Considerand simbolurile echiprobabile, puterea medie a semnalului digital in
cazul transmisiei binare bipolare este
![]() (3.17)
(3.17)
iar in cazul celei ternare
![]() (3.18)
(3.18)
ceea ce ne arata ca pentru a obtine
aceleasi performante, tensiunea semnalului ar trebui crescuta cu
![]() , adica de
aproximativ 1,225 ori fata de cazul binar.
, adica de
aproximativ 1,225 ori fata de cazul binar.
Exemplul 3 Sa calculam valoarea tensiunii semnalului de date intr-o
transmisie ternara in care bitul 0 este reprezentat prin nivelul ternar 0
iar bitii 1 sunt reprezentati alternativ prin nivelele ![]() si
si ![]() (codare AMI
(Alternate Mark Inversion) sau
bipolara nr.1) pentru a obtine aceeasi putere medie ca in cazul
transmisiei binare polare.
(codare AMI
(Alternate Mark Inversion) sau
bipolara nr.1) pentru a obtine aceeasi putere medie ca in cazul
transmisiei binare polare.
In transmisia binara bipolara valoarea medie a puterii transmise, daca probabilitatea de aparitie a bitului 1 este p, va fi
![]() (3.19)
(3.19)
in timp ce in codarea AMI,
![]() (3.20)
(3.20)
Pentru cazul echiprobabil ![]() avem
avem ![]() . Impunand
. Impunand
![]() (3.21)
(3.21)
Este interesant de remarcat ca intr-o transmisie
ternara, in care simbolurile ternare sunt echiprobabile, un simbol ternar
transporta ![]() biti de informatie, in timp ce
intr-o codare pseudoternara, de tipul AMI, in care simbolurile ternare
biti de informatie, in timp ce
intr-o codare pseudoternara, de tipul AMI, in care simbolurile ternare ![]() si
si ![]() sunt asociate cu bitul 1 si simbolul
ternar 0 cu cel binar 0, simbolul 0 ternar are aceeasi capacitate ca
si cel binar, iar
sunt asociate cu bitul 1 si simbolul
ternar 0 cu cel binar 0, simbolul 0 ternar are aceeasi capacitate ca
si cel binar, iar ![]() si
si ![]() reprezinta bitul 1, deci au aceeasi
capacitate ca si in cazul binar.
reprezinta bitul 1, deci au aceeasi
capacitate ca si in cazul binar.
Intr-o transmisie multinivel, sa zicem cu L nivele, nivelele sunt astfel distribuite incat sa apara in numar egal deasupra si dedesubtul axei, iar intre doua nivele adiacente sa avem aceeasi separare.
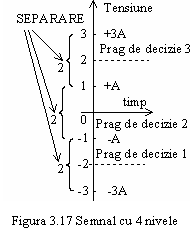
Exemplul 4 Fie o transmisie cu L = 4 nivele. Acestea sunt
reprezentate ca ![]() si
si ![]() si deobicei se accepta
conventia
si deobicei se accepta
conventia ![]() si
si ![]() , situatii reprezentate in figura 3.17.
Se observa ca intre doua nivele succesive exista o separare
, situatii reprezentate in figura 3.17.
Se observa ca intre doua nivele succesive exista o separare
![]() ,
jumatate din nivele sunt pozitive si jumatate negative iar
schema prezinta simetrie fata de axa orizontala. Se
observa ca pentru discriminarea celor 4 nivele sunt necesare 3
praguri de decizie (-2, 0 si +2) De exemplu, daca nivelul semnalului
este mai mare ca zero, dar mai mic decat +2, inseamna ca s-a transmis
nivelul +!.
,
jumatate din nivele sunt pozitive si jumatate negative iar
schema prezinta simetrie fata de axa orizontala. Se
observa ca pentru discriminarea celor 4 nivele sunt necesare 3
praguri de decizie (-2, 0 si +2) De exemplu, daca nivelul semnalului
este mai mare ca zero, dar mai mic decat +2, inseamna ca s-a transmis
nivelul +!.
In general, multe transmisii implica un numar par de nivele care este o putere intreaga a lui 2 (2, 4, 8, 16, 32, 64, 128 si 256 nivele).
 Presupunand
o transmisie cu L nivele (L numar par) egal distantate si
echiprobabile, sa calculam puterea medie a semnalului. Admitand separarea intre nivele de
valoare
Presupunand
o transmisie cu L nivele (L numar par) egal distantate si
echiprobabile, sa calculam puterea medie a semnalului. Admitand separarea intre nivele de
valoare ![]() ,
acestea pot fi considerate
,
acestea pot fi considerate ![]() . Lor le
corespund
. Lor le
corespund ![]() praguri de decizie
praguri de decizie ![]() .
Puterea medie a semnalului este
.
Puterea medie a semnalului este
![]() (3.22)
(3.22)
Tinand cont ca
![]() (3.23)
(3.23)
Rezulta:
![]() (3.24)
(3.24)
Exemplul 5 Sa calculam valorile nivelelor dintr-o transmisie cu 8 nivele echiprobababile si egal distantate, astfel ca sa avem aceeasi putere medie ca in transmisia binara polara.
![]() (3.25)
(3.25)
Din
conditia S=1 rezulta ![]()
Verificare
 8 Codarea
informatiei
8 Codarea
informatiei Din teoria transmisiunii informatiei se cunoaste faptul ca pe durate de timp mai lungi, proprietatile statistice ale zgomotului se manifesta mai bine, putand cunoaste cu mai multa precizie anumite proprietati statistice ale acestuia, de exemplu puterea. Aceasta inseamna fie o comunicatie digitala binara cu viteza mai mica de transmisie, cu avantajul evident al simplitatii echipamentului si dezavantajul debitului mic de transmitere a informatiei, fie o transmisie cu mai multe nivele, caz in care se mareste durata semnalului in detrimentul simplitatii echipamentului.
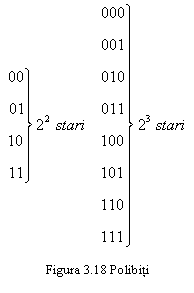
In cazul transmisiei digitale cu mai multe nivele
(polibinare), bitii din secventa de date se grupeaza cate 2
pentru a forma dibiti, sau cate 3 obtinand tribiti, carora
le corespund ![]() respectiv
respectiv ![]() stari
distincte si, generalizand, prin gruparea bitilor cate k se obtin
stari
distincte si, generalizand, prin gruparea bitilor cate k se obtin ![]() stari (figura 3.18).
stari (figura 3.18).
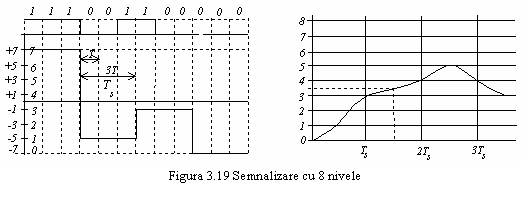

Viteza de transmisie ramanand aceeasi, dar in
intervalul elementar transmitandu-se k
biti in loc de un bit, durata intervalului elementar a crescut de k ori. In figura 3.19 este
ilustrata o forma de unda filtrata cu 8 nivele, fiecare
nivel fiind asociat unui tribit. Cele 8 nivele sunt alese simetric, 4 pozitive
si 4 negative, respectiv ![]() .
Daca tribitii sunt asociati celor 8 nivele conform codului binar
natural, poate apare urmatoarea situatie, ilustrata in figura
3.19.
.
Daca tribitii sunt asociati celor 8 nivele conform codului binar
natural, poate apare urmatoarea situatie, ilustrata in figura
3.19.
La momentele de sondare ![]() , datorita distorsiunilor de atenuare
si de faza precum si zgomotelor, nivelul semnalului este
falsificat, astfel incat la interpretarea formei de unda se poate face o
eroare.
, datorita distorsiunilor de atenuare
si de faza precum si zgomotelor, nivelul semnalului este
falsificat, astfel incat la interpretarea formei de unda se poate face o
eroare.
De exemplu, valoarea esantionului din forma de
unda poate fi interpretata ca reprezentand fie nivelul 3, fie nivelul
4. In codul binar natural avem: ![]() .
Eroarea introdusa afecteaza toti cei 3 biti ai tribitului
iar efectul ei asupra transmisiei este maxim.
.
Eroarea introdusa afecteaza toti cei 3 biti ai tribitului
iar efectul ei asupra transmisiei este maxim.
Pentru a minimiza efectul erorii ar trebui ca cele doua nivele particulare alaturate (adiacente) sa difere printr-un singur bit, ceea ce conduce la asocierea nivelelor de tensiune cu tribitii scrisi in codul Gray, in care doua elemente alaturate difera printr-un singur bit.
Din nefericire, cu cresterea lui k, avem un numar de ![]() de forme de unda particulare, carora
le sunt alocate secvente de date formate din k biti, iar complexitatea echipamentului creste.
de forme de unda particulare, carora
le sunt alocate secvente de date formate din k biti, iar complexitatea echipamentului creste.
 Exemplul
6 Sa consideram transmisia cu 4 nivele echiprobababile si egal
distantate, reprezentata in figura 3.20. Asociind cele 4 nivele cu
dibitii scrisi in codul binar natural, ei vin in ordinea 00, 0,1, 10,
11, de jos in sus. In cazul transmiterii simbolului +A asociat dibitului 10 in
prezenta interferentei intersimboluri, a distorsiunilor si
zgomotelor de tip aditiv, cea mai probabila eroare apare cu decizia
eronata ca in loc de +A s-a receptionat +3A sau -A. In acest ultim caz, in locul
dibitului 10 se obtine 01, ceea ce afecteaza ambii biti ai
dibitului, iar probabilitatea de eroare este crescuta.
Exemplul
6 Sa consideram transmisia cu 4 nivele echiprobababile si egal
distantate, reprezentata in figura 3.20. Asociind cele 4 nivele cu
dibitii scrisi in codul binar natural, ei vin in ordinea 00, 0,1, 10,
11, de jos in sus. In cazul transmiterii simbolului +A asociat dibitului 10 in
prezenta interferentei intersimboluri, a distorsiunilor si
zgomotelor de tip aditiv, cea mai probabila eroare apare cu decizia
eronata ca in loc de +A s-a receptionat +3A sau -A. In acest ultim caz, in locul
dibitului 10 se obtine 01, ceea ce afecteaza ambii biti ai
dibitului, iar probabilitatea de eroare este crescuta.
Daca asocierea nivelelor cu dibitii se face in codul Gray sau binar reflectat, adica in ordinea 00, 01,11,10 vedem ca 10 ar putea fi confundat fie cu 11, fie cu 01, adica in cazul erorii este afectat un singur bit din cadrul dibitului.
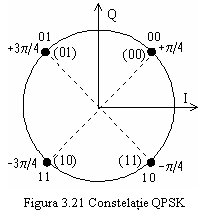 Acelasi
lucru poate fi observat din figura 3.21 unde este reprezentata
constelatia de faza a unui semnal QPSK, avand 4 valori ale fazei (
Acelasi
lucru poate fi observat din figura 3.21 unde este reprezentata
constelatia de faza a unui semnal QPSK, avand 4 valori ale fazei (![]() si
si
![]() ). In paranteze sunt trecute valorile
dibitilor scrise in codul binar natural. Posibilitatea unei erori duble, in cazul asocierii valorilor fazei cu
codul binar natural apare la confuzia lui 00 cu 11 si viceversa sau 01 cu
10 si invers.
). In paranteze sunt trecute valorile
dibitilor scrise in codul binar natural. Posibilitatea unei erori duble, in cazul asocierii valorilor fazei cu
codul binar natural apare la confuzia lui 00 cu 11 si viceversa sau 01 cu
10 si invers.
In cazul folosirii codului Gray nu mai exista posibilitatea unei erori duble, decat in cazul exceptional al unei perturbatii foarte puternice. Din aceasta cauza in transmisiile digitale se asociaza intotdeauna nivelele sau valorile aferente semnalului transmis cu multibitii sau polibitii scrisi in codul Gray.
Pentru a face sistemul de TD mai putin vulnerabil la erori, se recurge la introducerea de redundanta, alocand la k biti un numar mai mare de intervale n, cu n > k, procedeu denumit codare. Daca nu avem codare, la k biti corespund k intervale, si daca unul din bitii mesajului este receptionat eronat, acest lucru este echivalent cu receptionarea unui mesaj eronat, intrucat in locul combinatiei de k biti transmisi am obtinut alta combinatie valabila.
Daca la k
biti corespund n intervale
si unul din biti e receptionat eronat, secventa
receptionata nu mai corespunde cu una din cele transmise, intrucat
numai ![]() din cele
din cele ![]() posibile secvente constituie mesaje. Prin
codare intelegem deci procedeul de asociere a unui mesaj de k biti cu unul de n biti. La receptor are loc
operatia inversa, de decodare.
posibile secvente constituie mesaje. Prin
codare intelegem deci procedeul de asociere a unui mesaj de k biti cu unul de n biti. La receptor are loc
operatia inversa, de decodare.
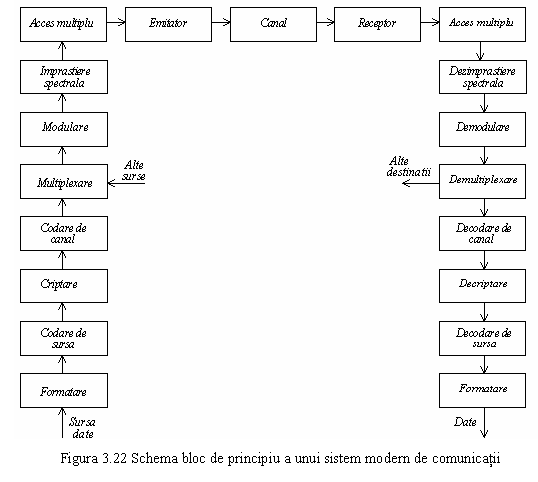
 Adaptarea semnalului la canalul de transmisie
poate implica inlocuirea semnalului digital de date cu unul analogic; procedeul
de asociere a unor forme de unda analogice secventelor de date de
intrare se numeste modulare, iar schema bloc a unui sistem de TD poate lua
forma din figura 3.22.
Adaptarea semnalului la canalul de transmisie
poate implica inlocuirea semnalului digital de date cu unul analogic; procedeul
de asociere a unor forme de unda analogice secventelor de date de
intrare se numeste modulare, iar schema bloc a unui sistem de TD poate lua
forma din figura 3.22.
Datele sunt aranjate intr-un anumit format, care sa permita interpretarea lor in mod unic de diversi utilizatori, care folosesc echipamente produse de fabricanti diferiti. Prin formatare datele sunt transformate in grupuri de simboluri care sa poata fi prelucrate prin operatii de procesare digitala.
Codarea de sursa in general se refera la conversia analog/digitala (A/D) a semnalelor analogice si la suprimarea redundantei, astfel ca transmisia sa fie cat mai eficienta. Intalnim de multe ori operatii de compactare sau compresie, care exploateaza redundanta existenta, reducand cat mai mult volumul efectiv de date ce urmeaza a fi transmis sau stocat.
Criptarea se refera la asigurarea secretului transmisiei astfel incat uitlizatorilor neautorizati sa nu li se permita accesul in sistem, care ar putea citi mesaje care nu le sunt destinate sau ar putea introduce informatii false, periculoase sau chiar distructive in sistem.
Codarea de canal asigura transmiterea eficienta a mesajelor, intr-o forma adaptata la canalul de transmisie. Ea asigura un compromis intre latimea benzii de tranmisie si/sau complexitatea codorului/decodorului pe de o parte si micsorarea probabilitatii de eroare (respectiv ratei erorilor) sau scaderea raportului S/Z necesare pentru a realiza o anumita viteza de transmisie.
Imprastierea spectrala asigura o vulnerabilitate mai mica a transmisiei la bruiaje si interferente, o secretizare mai buna precum si un acces multiplu al utilizatorilor la canalul de comunicatie caracterizat printr-o mai buna flexibilitate.
Prin multiplexare si acces multiplu pot fi transmise semnale cu debite si caracteristici diferite, provenite din surse diferite.
Nu toate aceste operatii pot fi intalnite intr-un sistem de comunicatii. Unele pot lipsi iar altele se pot combina sau distribui intre ele sau apare intr-o ordine diferita de cea prezentata.
Sa presupunem o transmisie digitala cu semnal codat dublu curent de tipul celui reprezentat in figura 3.23.
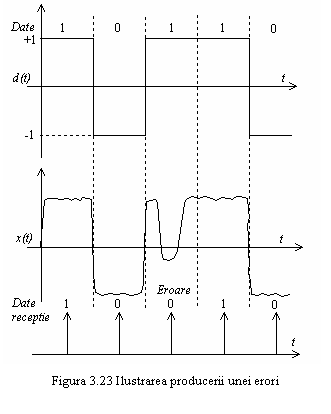 Canalul
de comunicatie atenueaza semnalul, il distorsioneaza si
introduce zgomote, denaturand semnalul receptionat. Forma de unda
este esantionata la mijlocul intervalului de bit, conform criteriului
I Nyquist, iar valoarea esantionului e comparata cu valoarea de
referinta, in acest caz 0. Datele sunt recuperate din forma de
unda receptionata printr-un proces de decizie. Daca
notam cu x valoarea
esantionului lui
Canalul
de comunicatie atenueaza semnalul, il distorsioneaza si
introduce zgomote, denaturand semnalul receptionat. Forma de unda
este esantionata la mijlocul intervalului de bit, conform criteriului
I Nyquist, iar valoarea esantionului e comparata cu valoarea de
referinta, in acest caz 0. Datele sunt recuperate din forma de
unda receptionata printr-un proces de decizie. Daca
notam cu x valoarea
esantionului lui![]() la momentul iT,
la momentul iT, ![]() , atunci
decizia se ia astfel,
, atunci
decizia se ia astfel,
q
daca: ![]() s-a transmis un bit 1,
s-a transmis un bit 1,
q
daca
![]() s-a transmis un bit 0.
s-a transmis un bit 0.
Zgomotul introdus de canalele de comunicatii are un caracter aleator si poate fi aproximat cu un zgomot gaussian, de valoare medie nula, avand functia densitate de probabilitate (f.d.p.) data de:
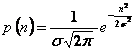 (3.26)
(3.26)
Probabilitatea de eroare depinde de raportul
semnal/zgomot ![]() ,
definit ca:
,
definit ca:
![]()
in cazul nostru, evident ![]()
![]() (3.27)
(3.27)
iar:
![]() (10.131)
(10.131)
Eroarea apare daca, in cazul transmiterii bitului 1
(nivel +1), nivelul zgomotului este mai mic decat -1, astfel incat avem ![]() ; fiind interpretat ca un bit 0, sau in cazul
transmiterii bitului 0 (nivel -1),
nivelul zgomotului depaseste valoarea +1 astfel incat:
; fiind interpretat ca un bit 0, sau in cazul
transmiterii bitului 0 (nivel -1),
nivelul zgomotului depaseste valoarea +1 astfel incat: ![]() ;
si este interpretat ca un bit 1.
;
si este interpretat ca un bit 1.
Probabilitatea de eroare ![]() este atunci:
este atunci:
![]() (3.28)
(3.28)
unde ![]() este probabilitatea ca variabila aleatoare
sa ia valoarea u.
este probabilitatea ca variabila aleatoare
sa ia valoarea u.
Presupunand zgomotul gaussian de valoare medie nula si cu f.d.p. data de (3.26), putem determina:
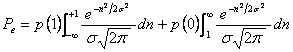 (3.29)
(3.29)
sau tinand cont de simetria para a f.d.p.
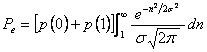 (3.30)
(3.30)
Evident, ![]() si deci:
si deci:
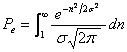 (3.31)
(3.31)
sau, facand schimbarea de variabila:
![]()
![]()
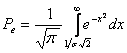 (3.32)
(3.32)
care se mai poate scrie ca:
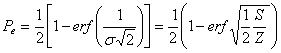 (3.33)
(3.33)
unde:
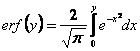 (3.34)
(3.34)
si este tabelata in anexa VII.

Ecuatiile (3.32) si (3.33) pot fi particularizate in urmatoarele doua cazuri extreme:
1.
Transmisia ideala, fara zgomot: ![]()
![]()
2. Transmisia in conditii foarte proaste, semnalul fiind inecat in zgomot:
![]()
deci un bit transmis va fi receptionat corect cu probabilitatea de 50%, aceeasi cu cea de a fi receptionat incorect. Acest caz este si cel mai defavorabil din punct de vedere al transmisiei.
Raportul S/Z poate fi considerat ca raportul dintre
puterea semnalului egala cu ![]() ,
daca transmisia bipolara implica nivelele
,
daca transmisia bipolara implica nivelele ![]() ,
raportata la zgomot, intr-o banda numeric egala cu viteza de bit
,
raportata la zgomot, intr-o banda numeric egala cu viteza de bit
![]() . Deci,
. Deci,
![]() iar
iar
![]() (3.35)
(3.35)
unde ![]() reprezinta energia de bit.
reprezinta energia de bit.
Un alt mod de a exprima
probabilitatea de eroare face apel la functia ![]() definita ca:
definita ca:
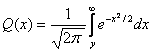 (3.36)
(3.36)
iar ![]()
si ![]() (3.37)
(3.37)
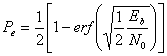 (3.38)
(3.38)
sau
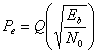 (3.39)
(3.39)
In cazul transmisiei unipolare (simplu curent),
reprezentata in figura 3.23.b, pentru bitii 1 si 0
echiprobabili, puterea medie a semnalului este ![]() , iar
raportul
, iar
raportul ![]() devine
devine ![]()
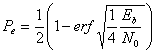
sau
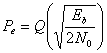 (3.40)
(3.40)
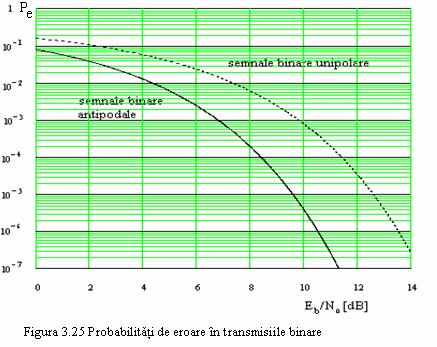
Probabilitatea de eroare, data de relatia (3.38) si (3.40) este reprezentata in figura 3.25.
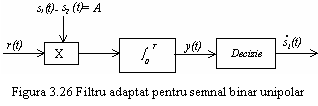
Vom considera mai intai cazul semnalelor binare unipolare descrise de
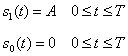 (3.41)
(3.41)
Semnalul ![]() este folosit pentru a transmite bitul de
informatie 1 si are amplitudinea
este folosit pentru a transmite bitul de
informatie 1 si are amplitudinea ![]() . Vom
presupune in continuare ca transmisia este perturbata de zgomot alb gaussian
si ca esantionarea se face cu perioada T. Recuperarea
informatiei insa se face cu ajutorul filtrului adaptat prezentat in
figura 3.26.
. Vom
presupune in continuare ca transmisia este perturbata de zgomot alb gaussian
si ca esantionarea se face cu perioada T. Recuperarea
informatiei insa se face cu ajutorul filtrului adaptat prezentat in
figura 3.26.
Semnalul de intrare ![]() este multiplicat cu diferenta semnalelor
utilizate pentru transmisie
este multiplicat cu diferenta semnalelor
utilizate pentru transmisie ![]() si integrat pe durata bitului T. La
sfarsitul perioadei de bit se ia decizia comparand rezultatul y(t) cu o
valoare de prag
si integrat pe durata bitului T. La
sfarsitul perioadei de bit se ia decizia comparand rezultatul y(t) cu o
valoare de prag ![]() .
Semnalul receptionat
.
Semnalul receptionat ![]() este de forma:
este de forma:
![]() (3.42)
(3.42)
Daca se transmite semnalul ![]() , componenta de semnal recuperata din
, componenta de semnal recuperata din ![]() este
este
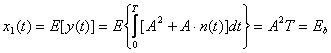 (3.43)
(3.43)
unde ![]() reprezinta operatorul speranta
matematica iar
reprezinta operatorul speranta
matematica iar ![]() .
Similar,
.
Similar,
![]()
Valoarea optima a pragului ![]() pentru detectie se alege ca:
pentru detectie se alege ca:
![]() (3.44)
(3.44)
Decizia se ia conform urmatoarei reguli:
q
daca iesirea corelatorului ![]() se decide ca s-a transmis bitul 1
(semnalul
se decide ca s-a transmis bitul 1
(semnalul ![]()
q
daca iesirea corelatorului ![]() se decide ca s-a transmis bitul 0
(semnalul
se decide ca s-a transmis bitul 0
(semnalul ![]()
Probabilitatea de eroare se obtine tinand cont ca filtrul adaptat maximizeaza raportul semnal/zgomot la iesirea sa, adica
![]() (3.45)
(3.45)
unde s-a presupus ca zgomotul are d.s.p.
definita bilateral ![]() , iar
, iar ![]() reprezinta energia semnalului
diferenta la intrarea filtrului adaptat
reprezinta energia semnalului
diferenta la intrarea filtrului adaptat
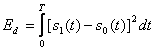 (3.46)
(3.46)
 iar probabilitatea de
eroare rezulta ca
iar probabilitatea de
eroare rezulta ca
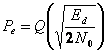 (3.47)
(3.47)
In cazul semnalului binar unipolar ![]() iar valoarea medie a energiei de bit este
iar valoarea medie a energiei de bit este ![]() . Rezulta
. Rezulta
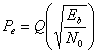 (3.48)
(3.48)
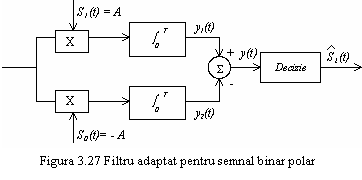 In cazul
transmisiei binare bipolare, semnalele utilizate sunt
In cazul
transmisiei binare bipolare, semnalele utilizate sunt
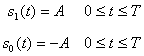 (3.49)
(3.49)
si pot fi caracterizate ca antipodale deoarece
![]() (3.50)
(3.50)
Semnalul receptionat ![]() este multiplicat cu cele 2 semnale
este multiplicat cu cele 2 semnale ![]() si
si ![]() iar decizia se ia asupra diferentei:
iar decizia se ia asupra diferentei:
![]() (3.51)
(3.51)
Deoarece semnalele sunt antipodale si echiprobabile,
pragul de decizie este ![]() .
Energia semnalului diferenta este
.
Energia semnalului diferenta este
![]() (3.52)
(3.52)
iar probabilitatea de eroare rezulta din (7.21) ca
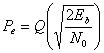 (3.53)
(3.53)
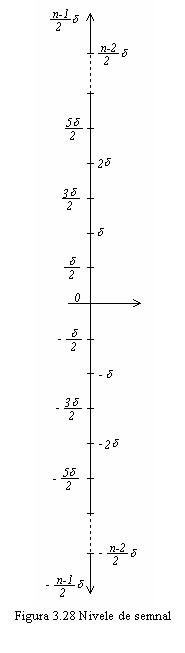
Fie o transmisie multinivel cu M nivele (M - numar
par), egal distantate si echiprobabile, perturbate de un zgomot
gaussian de valoare medie nula si varianta ![]() .
Presupunand separarea intre nivele
.
Presupunand separarea intre nivele ![]() ,
acestea pot fi considerate:
,
acestea pot fi considerate: ![]() ,
carora le corespund pragurile de decizie
,
carora le corespund pragurile de decizie ![]() ,
asa cum se arata in figura 3.28.
,
asa cum se arata in figura 3.28.
Puterea
medie a semnalului este: 
![]() (3.54)
(3.54)
Raportul ![]() va fi atunci:
va fi atunci:
![]() (3.55)
(3.55)
Probabilitatea de eroare (pentru ![]() nivele) la detectia semnalului multinivel
va fi
nivele) la detectia semnalului multinivel
va fi ![]() ,
exceptand nivelele extreme din figura 3.28, unde devine
,
exceptand nivelele extreme din figura 3.28, unde devine ![]() si respectiv
si respectiv ![]()
Probabilitatea medie de eroare devine:
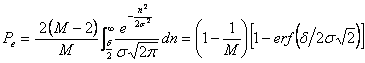 (3.56)
(3.56)
Din (3.55) avem
![]() ,
,
iar
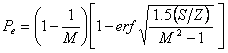 (3.57)
(3.57)
sau
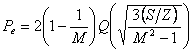 (3.58)
(3.58)
Tinand cont de faptul ca transmisia cu mai multe nivele implica organizarea informatiei in cuvinte de k biti, unde k rezulta din
![]()
iar ![]() (3.59)
(3.59)
relatia (3.58) este modificata pentru a permite o comparare a diferitelor tipuri de transmisii luand ca referinta energia transportata de un bit si devine
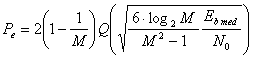 (3.60)
(3.60)
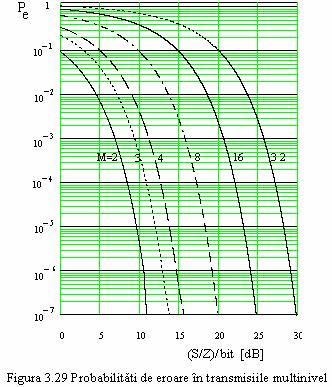
Ea este reprezentata in figura 3.29, pentru diverse
valori ale lui M, M=2, 3, 4, 8, 16 si 32. Prin ![]() s-a notat cantitatea
s-a notat cantitatea ![]()
TD au adoptat si imbunatatit procedeele de transmisie in curent continuu, folosite in telegrafie, pe linia de transmisie circuland impulsuri de curent obtinute fie prin intreruperea unui curent electric (telegrafie simplu curent), fie prin inversarea sensului acestuia (dublu curent), ca in figura 3.16.
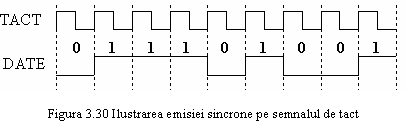

In TD
datele sunt emise sincron, pe un semnal de clock sau tact cu frecventa de
emisie![]() (figura 3.30).
(figura 3.30).
Momentele semnificative sunt asociate unui anumit front al tactului. TD se clasifica in:
q transmisii sincrone (izocrone)
q transmisii asincrone sau aritmice (START - STOP).
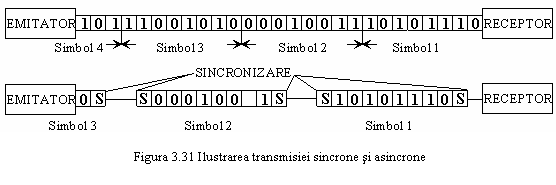
 In
TD sincrona sau izocrona toate starile semnificative au
aceeasi durata T, iar doi
biti oarecare dintr-un mesaj sau apartinand la doua mesaje
diferite sunt separati de un interval de timp multiplu al duratei
bitului T (figura 3.31).
In
TD sincrona sau izocrona toate starile semnificative au
aceeasi durata T, iar doi
biti oarecare dintr-un mesaj sau apartinand la doua mesaje
diferite sunt separati de un interval de timp multiplu al duratei
bitului T (figura 3.31).
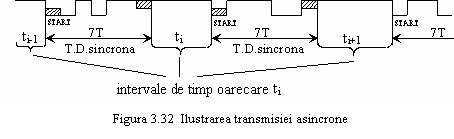

In transmisia asincrona sau START-STOP (aritmica) se emit mesaje de date sincrone, de durata cunoscuta si mica, separate de intervale de timp de durate oarecare (vezi figura 3.25). Inceputul si sfarsitul mesajelor sunt denumite START si respectiv STOP si se codeaza in mod unic (figura 3.32).
TD sincrona implica
obtinerea unui semnal cu frecventa de emisie a datelor ![]() ,
care este folosit pentru recunoasterea datelor transmise: cea
asincrona implica refacerea sincronizarii de bit pentru fiecare
caracter transmis, cu tolerante mai largi.
,
care este folosit pentru recunoasterea datelor transmise: cea
asincrona implica refacerea sincronizarii de bit pentru fiecare
caracter transmis, cu tolerante mai largi.
 Dupa
modul de ocupare a benzii canalului de transmisie deosebim:
Dupa
modul de ocupare a benzii canalului de transmisie deosebim:
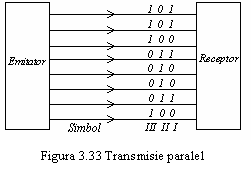
q TD serie
q TD paralel.
In cele serie, spectrul de frecventa a semnalului de date ocupa intreaga banda a canalului. In sistemele paralel se transmit simultan doua sau mai multe semnale de date, canalele de date fiind de obicei multiplexate si transmise sincron (fig. 3.33). In general, sistemele serie sunt mai putin complexe si mai usor de implementata decat cele paralel, si in consecinta sunt mai ieftine.
Dupa modul de functionare, TD se clasifica in transmisii
q simplex,
q semi-duplex
q duplex.
TD simplex se caracterizeaza prin aceea ca transmisia se poate efectua intr-un singur sens. TD semi-duplex permit transmisia datelor in ambele sensuri, dar nu simultan. TD duplex realizeaza transmisiunea simultana in ambele sensuri.
Luand un exemplu din viata curenta, am putea spune ca o scara rulanta (escalator) este un sistem simplex (prin inversarea semnalului devine semi-duplex), un ascensor este un sistem semi-duplex iar scarile un sistem duplex. TD se mai pot clasifica in
q transmisii in banda de baza
q cu modulare-demodulare.
Semnalele in banda de baza au spectrul in general extins pana la frecvente foarte joase, chiar 0 Hz (c.c.) si transporta informatia sub forma de valori luate la anumite momente de timp.
In TD cu modulare-demodulare spectrul semnalului de date original (in banda de baza) este translat sau transformat neliniar, pentru a ocupa mai bine banda canalului de transmisie.
Tehnicile de modulare folosite in sistemele de comunicatii mobile au fost la inceput cu anvelopa constanta, adica foloseau modulatia exponentiala de faza sau frecventa). Avantajele semnalelor cu anvelopa constanta sunt urmatoarele:
o Etajul final amplificator RF nu trebuie sa fie liniar si ca urmare poate fi utilizat eficient aproape de saturatie, cu randament maxim;
o Nu este necesara supradimensionarea dispozitivelor semiconductoare utilizate in amplificatorul final RF;
o Nu este necesara supradimensionarea bateriilor de alimentare in cazul echipamentelor portabile.
Dezavantajul principal al tehnicilor de modulare cu anvelopa constanta il constituie faptul ca nu sunt eficiente din punct de vedere spectral. Tehnicile actuale utilizate in sistemele de comunicatii mobile utilizeaza o modulatie combinata de faza si amplitudine si au anvelopa variabila. Pentru evitarea degradarii performantelor, amplificatorul final trebuie liniarizat. Deoarece amplificatoarele liniare nu au randament bun se utilizeaza un amplificator neliniar, care asigura un randament ridicat si un circuit care sa elimine distorsiunile.
Fie X(t), Y(t) doua procese aleatoare independente, stationare in sens larg avand functiile de corelatie RX(t) si RY(t)
a. Daca Z(t) = X(t). Y(t) , calculati RZ(t).
b. Calculati SZ(f).
c. Daca SX(f) = 10 P(f /200), iar Y(t) = 5 cos(50 p t + F F uniform distribuita pe intervalul (- p p), calculati RZ(t) si SZ(f). Reprezentati grafic SZ(f).
Introducere in comunicatiile digitale
1 Introducere
2 Interferente si distorsiuni
3 Interferenta intersimboluri
4 Diagrama in forma de ochi
5 Efectul Doppler
6 Propagare multicai (multipath) si fading
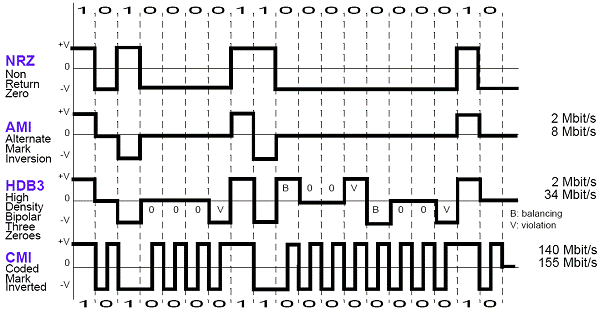
7 Reprezentarea electrica a informatiei digitale
8 Codarea informatiei
9 Tipuri de transmisiuni
10 Detectia cu filtru adaptat
11 Probabilitatea de eroare pentru TD multinivel in banda de baza
12 Tipuri de transmisiuni
13 Probleme
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2879
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved