CONTROLUL VECTORIAL AL MOTORULUI ASINCRON CU MODULATIE IN LATIME A IMPULSURILOR (PWM)

CONTROLUL VECTORIAL AL MOTORULUI ASINCRON CU MODULATIE IN LATIME A IMPULSURILOR (PWM)

1.1 Controlul vectorial cu modulatie naturala in latime a impulsurilor, cu comparator sinusoida-triunghi

Circuitul de modulatie naturala se poate realiza atat analogic, cat si numeric. El se implementeaza practic foarte simplu cu ajutorul a trei comparatoare fara histerezis (sau cu un histerezis foarte mic, pentru a elimina comutatiile multiple) si a unui generator de unda triunghiulara de referinta, avand amplitudinea constanta si axata fata de zero.

Frecventa de comutatie a invertorului de tensiune este determinata de frecventa undei de referinta.

Comparatorul se poate realiza analogic, cu amplificator operational cu reactie pozitiva. Pe intrarea comparatorului se aplica un semnal sinusoidal de amplitudine si frecventa variabile. In cazul reglarii vectoriale, intrarea este reprezentata de tensiunea statorica impusa, de exemplu u_sa*. Cu ajutorul amplitudinii semnalului sinusoidal se modifica adancimea de modulare, avand

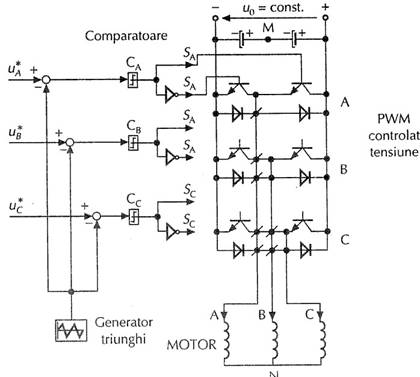
Fig. 6.20

Schema bloc a modulatorului in latime a impulsurilor cu comparator sinusoida-triunghi (modulatie naturala)

ca efect modificarea valorii efective a tensiunii la bornele motorului asincron. Unda triunghiulara se genereaza folosind numaratoare in inel. Acest circuit este prezentat in figura 6.20.

1.2 Modularea vectoriala spatiala a tensiunii la iesirea din invertorul de tensiune

In figura 6.21 se poate observa ca invertorul de tensiune face posibila conectarea fiecarei faze la potentialul pozitiv sau la cel negativ al sursei de alimentare de tensiune continua constanta, u_d. Fiecarei linii a invertorului i se poate asocia un comutator ideal.

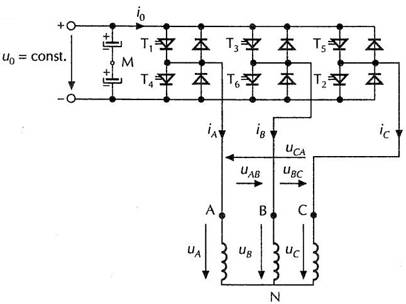
Fig. 6.21

Invertorul de tensiune pentru alimentarea motorului asincron

Schema echivalenta pentru invertorul trifazat este prezentata in figura 6.22, a.

Componentele fazorului spatial al tensiunii statorice in sistemul de referinta statoric fix α-β sunt calculate in functie de tensiunile de faza, sub forma de mai jos:

(6.16)

Daca punctul neutru N al motorului si punctul M nu sunt conectate (fig. 6.22, a), sunt posibile opt moduri de conductie ale invertorului. In sase din modurile de conductie, invertorul determina tensiuni de iesire diferite de zero, iar celelalte doua moduri determina tensiuni nule la bornele sarcinii. In acest caz, fiecare infasurare statorica a motorului este conectata fie la potentialul pozitiv, fie la cel negativ al sursei de alimentare.

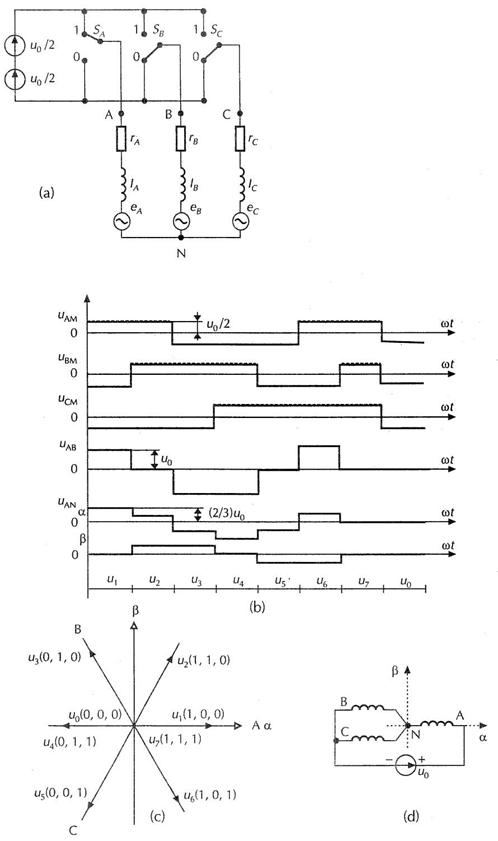
Fig. 6.22

Reprezentarea tensiunilor la bornele invertorului de tensiune:

(a) schema echivalenta a invertorului care alimenteaza motorul asincron;

(b) tensiunile de iesire;

(c) tensiunile de iesire reprezentate ca fazori spatiali;

(d)exemplu de circuit corespunzator vectorului u₁(

Tensiunea de iesire la bornele invertorului poate fi reprezentata cu ajutorul unui fazor spatial, determinat de relatia:

(6.17)

0 v=0,7

unde: u_d - U_d / U_sn este tensiunea continua de alimentare in unitati relative.

Pentru modul de lucru cu sase pulsuri, vectorul tensiunii ramane constant in timp pe o perioada de ω_st = π/3 si apoi la fiecare comutatie acesta isi schimba pozitia cu π/3.

Starea comutatoarelor bratelor invertorului "A', "B', "C', S_v(S_A, S_B, S_C) corespunde fiecarui vector u_v.

Pentru s = 1, comutatorul este pe pozitia "sus' si pentru s = 0, comutatorul este pe pozitia "jos'.

Astfel, de exemplu, vectorul u₁(0, 0, 0) reprezinta starea prezentata in figura 6.22, a (tiristoarele T₁, T₆ si T₂ sunt in conductie (fig. 6.21)) si circuitul echivalent este prezentat in figura 6.22, d. In consecinta, tensiunea de iesire a invertorului poate fi asimilata cu un vector care ocupa sase pozitii constante. Pozitiile intermediare sunt posibile daca sunt comutatii intre doi vectori vecini. Amplitudinea vectorului de tensiune se poate modifica, modificand tensiunea din circuitul intermediar, u_d , iar daca u_d=ct., aceasta poate fi redusa prin comutatii pe cele doua stari de tensiune nula u_Q si u_r. . Aceasta metoda este adecvata implementarii numerice.

Se pune problema de a se gasi starile comparatoarelor bratelor invertorului "A', "B', "C' (S_A, S_B, S_C), astfel incat valoarea vectorului de tensiune u sa fie egala cu valoarea impusa a acestuia, u_s*, pe perioada de esantionare T_s.

Implementarea vectorului tensiunii statorice de comanda u_s* = [u_s*, q_su*} (fig. 6.23, a) va fi prezentata sub forma unui exemplu de procedura pentru modularea vectoriala. Vectorul tensiunii statorice impuse, u_s* este presupus a fi constant pe perioada de esantionare 7_s. Pentru cazul considerat, vectorul se gaseste in primul sector. Pentru a reduce armonicile de tensiune, vectorii vecini u₀, u₁, u₂ si u₇ din primul sector trebuie folositi pentru implementarea

vectorului u_S*. Pentru a obtine o frecventa minima de comutatie a fiecarei linii a invertorului, trebuie sa se realizeze comutatia unei singure linii a invertorului. Aceste conditii se intalnesc daca, pornind de la starea de zero, bratele invertorului sunt comutate catre o alta stare de zero. Astfel, pentru vectorul u_S* din primul sector, secventa de comutatie trebuie sa fie:

(fig. 6.23,b)

Hexagonul cu linie punctata din figura 6.23, a indica limita permisa pentru valoarea vectorului tensiunii statorice impuse u'_s, dar frecventa de comutatie maxima permisa, f_max, impune si alte categorii de restrictii. Timpul minim pentru aplicarea secventei vectorului nul este determinat de aceasta frecventa maxima de comutatie:

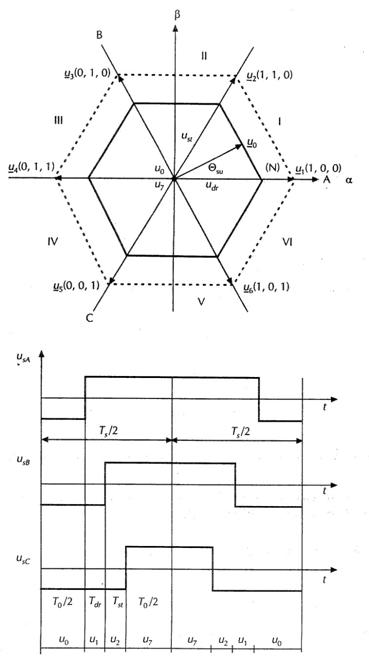Fig. 6.23

Principiul modularii vectoriale:

a) vectorii de tensiune la iesirea invertorului de tensiune;

b) modelul optim al pulsurilor de tensiune.

(6.18)

Aceasta restrictie este indicata in figura 6.23, a prin hexagonul cu linie continua. Procedura de calcul al timpilor cat sunt aplicati vectorii din stanga, dreapta si zero este urmatoarea:

- determinarea legaturii intre pozitia Θ_su, fazorului spatial al tensiunii statorice impuse u_s* si numarul N al sectorului de 60;

, unde N = I,II,III ,VI (6.19)

- calculul amplitudinii maxime permise a fazorului tensiunii statorice:

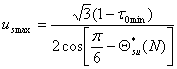(6.20)

unde: si, daca , atunci

- durata vectorilor din dreapta, stanga si zero pentru sectorul necesar sunt date de:

Modularea vectoriala conduce la un continut scazut de armonici de curent.

Reglarea si controlul vectorial in tensiune al motorului asincron orientat dupa fluxul rotoric

2.1 Comanda si reglarea vectoriala directa

In cazul sistemelor vectoriale cu invertoare de curent sau cu invertoare de tensiune PWM comandate in curent, controlul curentului se face in coordonate statorice (buclele de curent sunt in coordonate statorice). Ecuatiile de tensiune statorica nu intervin in modelul necesar comenzii in curent si deci nu pot influenta raspunsul dinamic al sistemului. La puteri mari, controlul vectorial in curent cu invertoare de tensiune PWM nu mai poate fi implementat, deoarece trebuie redusa frecventa de comutatie pentru micsorarea pierderilor (frecventa de comutatie uzuala este in limitele 300 -1000 Hz).In acest caz, invertorul trebuie comandat in tensiune, fiind necesara utilizarea ecuatiilor de tensiune statorica.

Se vor prezenta in continuare doua sisteme vectoriale directe cu invertor PWM comandat in tensiune.

2.1.1 Sistem vectorial direct cu invertor PWM comandat in tensiune

Ecuatiile de tensiune statorica pe cele doua axe d-q ale sistemului orientat sunt:

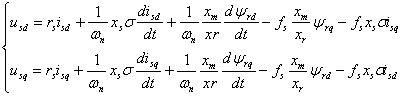
Avand in vedere ca orientarea masinii se face dupa fluxul :

si sistemul de ecuatii (6.22) devine: 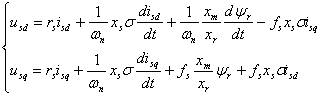   (6.23)

rezultand astfel sistemul de ecuatii necesar pentru decuplarea motorului asincron orientat dupa fluxul rotoric comandat in tensiune.

Daca sistemul de reglare contine bucle de reglare separate de flux si de cuplu, ecuatiile de tensiune pentru decuplarea motorului asincron se pot scrie sub forma simplificata:

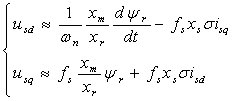(6.24)

Frecventa statorica, f_s, necesara in calculul celor doua componente, este o marime dificil de determinat si se poate face o a doua simplificare, f_s n, erorile introduse in raspunsul dinamic al sistemului fiind nesemnificative. Ecuatiile (6.24) devin:

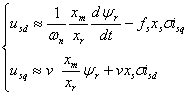(6.25)

Ecuatiile de tensiune pentru decuplarea tensiunilor (6.25) sunt valabile atat pentru zona de flux constant, cat si in cea de slabire de camp.

2.1.2 Sistem vectorial direct cu invertor PWM comandat in tensiune si controlul curentului in coordonate de camp

Curentul statoric, in acest caz, este reglat in coordonate de camp d- q. Sunt prezente doua bucle de reglare a componentelor ortogonale i_sd*, i_sq* Sursa de alimentare a motorului asincron de tractiune este, de asemenea, un invertor de tensiune PWM, la care se pot aplica diferite strategii de modulare. Daca invertorul PWM lucreaza cu frecvente de comutatie moderate (300 -1000 Hz), este necesar, de asemenea, blocul de decuplare a tensiunilor (sistemul de ecuatii 6.25). Daca frecventa de comutatie este mai mare decat 2000 Hz (sau in cazul sistemelor de reglare numerice, frecventa de esantionare este suficient de mare), acest bloc de decuplare poate fi omis. Se va demonstra in continuare aceasta afirmatie.

Deoarece sistemul de reglare trebuie sa asigure functionarea la flux rotoric constant, ecuatiile (6.23) devin:

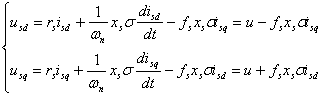(6..26)

Avand in vedere ecuatiile (6.26), sistemul de control al curentilor in coordonate de camp complet decuplat arata ca in figura 6.24.

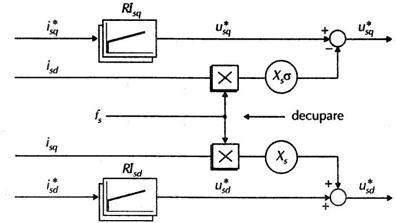
Fig. 6.24

Controlul curentilor in coordonate de camp cu decuplarea tensiunilor statorice

Sistemul de ecuatii (6.26) se poate pune sub forma ecuatiilor de stare:

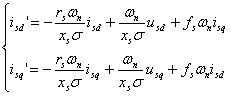(6.27)

Reprezentarea matriceala a sistemului (6.27) este urmatoarea:

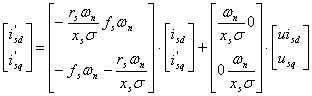(6.28)

Se discretizeaza sistemul continuu (6.28), punandu-se sub forma urmatoare:

(6.29)

unde: 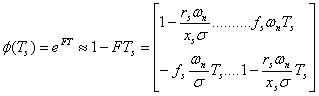(6.30)

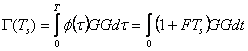(6.31)

Pe perioada de esantionare T_s se poate considera frecventa f_s = ct.

Astfel devine:

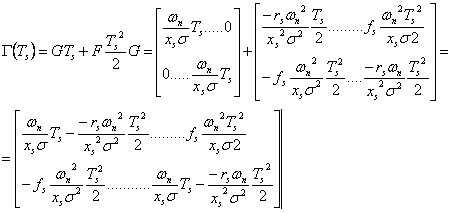
(6.32)

Sistemul de ecuatii de stare (6.32) se scrie acum sub forma:

(6.33)

Deoarece f_skT_s -> 0

T_se [100 10 0 ms ]-sistem numeric;

T_s << 1-sistem continuu

(6.34)

Sistemul de control al curentilor in coordonate de camp se realizeaza cu doua regulatoare de curent de tip PI (unul pentru i_sd si celalalt pentru i_sq), iesirile acestor doua regulatoare(tensiunile de referinta in coordonate de camp,u_sd,u_sq ) devenind astfel variabile efective de control.

3 Reglarea si controlul vectorial in tensiune al motorului asincron orientat dupa fluxul statoric

3.1 Reglarea vectoriala directa cu invertor PWM comandat prin comutatie naturala

Sistemele vectoriale de reglare a motorului asincron orientat dupa fluxul rotoric au la baza ecuatia fazoriala a tensiunii rotorice in sistemul de referinta orientat d - q, care conduce la numeroase avantaje pentru acest mod de orientare. Prin urmare, avantajul, specific unui sistem de reglare vectoriala a motorului asincron orientat dupa fluxul statoric, trebuie cautat la aplicarea ecuatiei fazoriale a tensiunii statorice. Sursa fiind de tensiune, trebuie determinate marimile de comanda, care sunt componentele ortogonale ale fazorului tensiunii statorice in sistemul orientat d_λ - q_λ. Aceste componente se exprima in functie de curentul i_λsq corespunzator cuplului electromagnetic si de curentul i_ms de magnetizare corespunzator fluxului statoric.

Ecuatia fazoriala a tensiunii statorice in sistemul orientat este:

(6.35)

care, scrisa pe componente, devine:

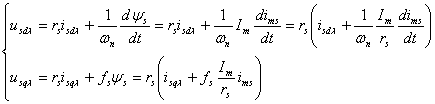(6.36)

Avand in vedere sistemul de ecuatii (6.36), se determina regulatorul - sistem de control sub forma din figura 6.25.

Analizand cele doua ecuatii (6.36) se poate vedea ca termenul care prezinta importanta pentru determinarea marimilor de comanda in tensiune a convertorului este cel care contine produsul (in regim stabilizat ). Comparand aceste relatii cu cele echivalente de la sistemul de reglare cu orientare dupa v se poate vedea ca, in cazul de fata, calculul marimilor de comanda este cel mai simplu posibil. Astfel, sistemul de reglare nu este influentat de variatia rezistentei rotorice iar efectul variatiei rezistentei statorice la frecvente nu prea joase poate fi neglijat.

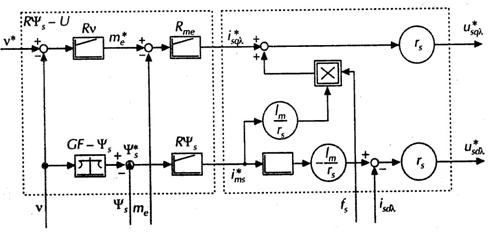
Fig. 6.25

Schema bloc a regulatorului pentru comanda vectoriala directa a motorului asincron orientat dupa fluxul statoric, cu invertor de tensiune PWM, comandat in tensiune

Din cele aratate mai sus se constata ca acest mod de control prezinta o importanta deosebita, datorita simplitatii calculului marimilor de comanda.

Schema de reglare vectoriala a motorului asincron orientat dupa fluxul statoric cu invertor de tensiune PWM, comandat in tensiune, se poate pune sub forma din figura 11.25.

3.2 Comanda si controlul vectorial a! cuplului motorului asincron

Prin controlul vectorial al cuplului se intelege controlul vectorial direct al fluxului. Cu ajutorul a doua regulatoare cu histerezis, care determina cei sase

vectori de tensiune ( u₁, u₂,, u₆) si cei doi vectori nuli (u_o,u₇), cu ajutorul carora se comanda invertorul de tensiune PWM. Acest control vectorial necesita

estimarea fluxului statoric si a cuplului electromagnetic, care se face cu ajutorul tensiunilor si curentilor statorici masurati (modelul u_s - i_sdin figura 6.26).

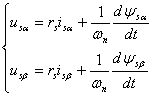(6.37)

Structura de baza a controlului vectorial al cuplului cu invertor de tensiune PWM este cea prezentata in figura 6.26.

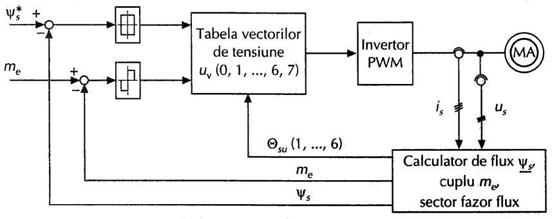
Fig. 6.26

Structura de baza a controlului vectorial al cuplului

Acest mod de reglare este adecvat pentru controlul pozitiei sau turatiei, conducand la reglare stabila pana la aproximativ 0,1 rot/ora.

Proprietatile acestui mod de reglare sunt urmatoarele:

- nu este necesara utilizarea unui modulator separat al tensiunii pentru comanda invertorului PWM;

- nu sunt necesare bucle de reglare a curentului statoric;

- nu sunt necesare transformari de axe si sistem;

- este necesara masurarea fluxului statoric si a cuplului electromagnetic, controlul vectorial efectuandu-se direct;

- este adecvat controlului numeric (care este indispensabil pentru acest caz).

Deoarece comanda invertorului PWM se face cu ajutorul vectorilor de tensiune statorica (u₁,u_2,, u_6,u₀,u₇), trebuie indicat modul de determinare a acestor opt vectori, astfel incat sa fie asigurate fluxul statoric si cuplul electromagnetic necesare.

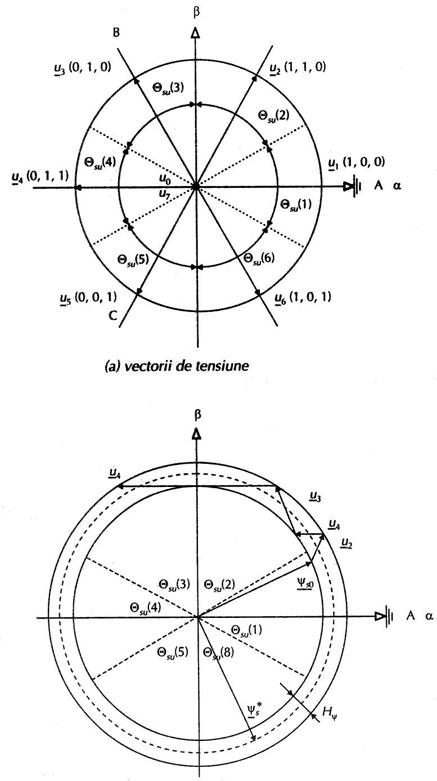
Fig. 6.27

(a) vectorii de tensiune

(b) controlul fluxului statoric si rotirea acestuia Selectia vectorilor de tensiune statorica pentru controlul fluxului statoric

(c) selectia vectorilor de tensiune necesari Selectia vectorilor de tensiune statorica pentru controlul fluxului statoric

Problema care se ridica este aceea de a selecta vectorii de tensiune necesari pentru controlul fluxului statoric. Se utilizeaza ecuatia vectoriala a tensiunii statorice in sistemul de referinta fix a - b,neglijand rezistenta statorica(r=0)

(6.39)

Directia vectorului este data de vectorul (v=1,2,...6,0,8) , (fig, 6.27, a).

Astfel, variatia fluxului statoric se realizeaza de-a lungul vectorului de tensiune statorica cu care este comandat invertorul. Pentru a mentine amplitudinea fazorului fluxului statoric constanta intre doua cercuri limita, trebuie aplicat vectorul adecvat de tensiune (fig. 6.27, b). Acest vector de tensiune adecvat depinde de pozitia initiala a fazorului fluxului statoric , care trebuie cunoscut numai in sensul prezentei lui intr-unui din cele sase sectoare de 60 (fig. 6.27, a). Pozitia poate fi determinata cu simple comparatoare.

Componentele ortogonale ale fazorului fluxului statoric,in sistemul fix α-β

Cu ajutorul tabelului de mai jos se obtin semnele componentelor si pozitia

Informatia cu privire la eroare de flux si la pozitia sa, conduce la selectia adecvata a vectorului de tensiune statorica, care depinde, de asemenea, de semnul cuplului electromagnetic (fig. 6.27, c). Vectorul de flux este accelerat pentru a produce cuplu pozitiv si este accelerat pentru a produce cuplu negativ. Pentru comanda nula de cuplu, este selectat unul din cei doi vectori nuli de tensiune. Astfel, accelerarea fluxului statoric inseamna, de fapt, cresterea frecventei statorice, si, implicit, a alunecarii.

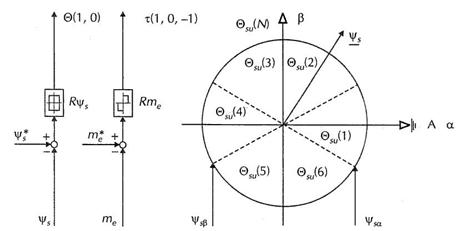Fig 6.28

Tabelul si modul de determinare a vectorilor tensiunii statorice

si a cuplului electromagnetic. Cand se aplica vectorii nuli de tensiune, fluxul statoric isi opreste rotirea si scade incet, in timp ce raspunsul tranzitoriu de cuplu se incetineste. In final se obtine tabelul vectorilor de tensiune ca in figura 6.28. De asemenea, sistemul vectorial de control al cuplului este prezentat in figura 6.28.

Erorile de flux statoric si de cuplu electromagnetic reprezinta intrarile celor doua regulatoare cu histerezis. Regulatorul de flux este un comparator cu histerezis cu doua nivele, in timp ce regulatorul de cuplu este un comparator cu histerezis cu trei nivele. Semnalele numerice la iesirile celor doua regulatoare se definesc astfel:

- regulatorul de flux statoric,

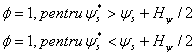(6.41)

- regulatorul de cuplu R_m

r = 1 pentru m*_e > m_e+ H_m

r = 0 pentru m*_e =m_e

r = -1 pentru m*_e < m_e - H_m

Informatia cu privire la eroarea de flux si la pozitia sa, conduce la selectia adecvata a vectorului de tensiune statorica, care depinde, de asemenea, de semnul cuplului electromagnetic (fig. 6.27, c). Acest lucru se intampla deoarece vectorul de flux este accelerat pentru a produce cuplu pozitiv si este decelerat pentru a produce cuplu negativ. Pentru comanda nula de cuplu este selectat unul din cei doi vectori nuli de tensiune. Astfel, accelerarea fluxului statoric inseamna, de fapt, cresterea frecventei statorice, f, si implicit a alunecarii si a cuplului electromagnetic. Cand se aplica vectori nuli de tensiune, fluxul statoric isi opreste rotirea si scade incet, in timp ce raspunsul tranzitoriu de cuplu se incetineste. in final, se obtine tabela vectorilor de tensiune (fig. 6.28). De asemenea, sistemul vectorial de control al cuplului este prezentat in fig. 6.29.

Erorile de flux statoric si de cuplu electromagnetic reprezinta intrarile celor doua regulatoare cu histerezis. Regulatorul de flux este un comparator cu histerezis cu doua niveluri, in timp ce regulatorul de cuplu este un comparator cu histerezis cu trei niveluri.

Caracteristicile unui astfel de sistem includ:

- realizarea curentilor si fluxurilor sinusoidale, continutul de armonici fiind determinat de latimea benzilor de histerezis H_m si H_w;

- functionare posibila numai in cazul PWM (nu este posibila comanda in sase pulsuri) si, in consecinta, este necesara o rezerva de tensiune de alimentare a invertorului;

- frecventa de comutatie > 2 KHz, care depinde de latimea benzilor de histerezis H_m si H_y. Controlul direct al cuplului electromagnetic poate fi, de asemenea, aplicat in cazul utilizarii invertoarelor rezonante.

Au fost prezentate in acest capitol principii si sisteme de comanda vectoriale reprezentative pentru controlul in tensiune al motorului asincron. Controlul in curent lucreaza bine la viteze joase, dar controlul in tensiune este superior la viteze ridicate (in zona de slabire de camp).

Se pot realiza chiar combinatii ale metodelor vectoriale de reglare pentru a se imbunatati raspunsul sistemului.

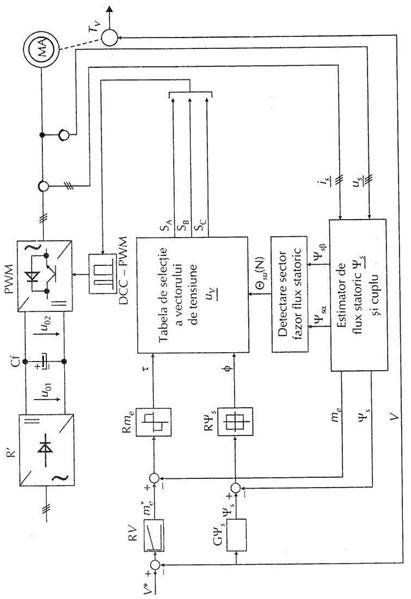
Fig. 6.29

Sistem de control vectorial al cuplului motorului asincron orientat dupa fluxul statoric, alimentat cu invertor de tensiune PWM