Efectul piroelectric

Efectul piroelectric

I. Introducere

Piroelectricitatea este proprietatea unor anumite cristale anizotrope prin care polarizarea electrica spontana depinde de temperatura. Substantele care prezinta aceasta proprietate se numesc piroelectrice, iar aparitia sarcinilor electrice la suprafata unui astfel de material in urma incalzii sau racirii lui se numeste efectul piroelectric. Una dintre aplicatiile piroelectricitatii este in dispozitivele de detectie a radiatiilor infrarosii si milimetrice, folosite de exemplu in detectia de la distanta a miscarii oamenilor si animalelor.

Printre materialele piroelectrice cele mai comune se numara cuartul, turmalina, unele substante monocristaline (tantalat de litiu etc.), materiale ceramice si unii polimeri, precum si o serie de substante organice ca tesuturile de os si de tendon si colagenul.

Efectul piroelectric consta in aparitia de sarcini electrice de semne contrare la suprafetele opuse ale materialului atunci cind acesta este incalzit sau racit. Sarcinile electrice apar ca urmare a cresterii sau scaderii polarizarii electrice din volumul materialului.

Exista o legatura strinsa intre piroelectricitate si piezoelectricitate (aparitia polarizarii electrice in urma deformarii mecanice), una din consecintele acestei legaturi fiind faptul ca toate materialele piroelectrice sint in acelasi timp si piezoelectrice. Conditia necesara dar nu suficienta pentru ca un cristal sa fie piroelectric este ca acesta sa apartina unei clase necentrosimetrice. Din cele 32 de clase cristaline, 21 sunt necentrosimetrice, 20 includ cristalele piezoelectrice, 10 din cele douazeci prezentand fenomenul de piroelectricitate.

Efectul piroelectric are la nivel molecular doua componente:

• Efectul piroelectric direct consta in aparitia polarizarii electrice strict sub influenta temperaturii, fara interventia deformarilor mecanice.
• Efectul piroelectric indirect se produce in doua etape: modificarea temperaturii produce deformari si tensiuni mecanice care la rindul lor determina polarizarea electrica prin piezoelectricitate.

Coeficientul piroelectric arata ce polarizare electrica se obtine la variatia cu o unitate a temperaturii:

dD=p dθ

unde D este polarizarea electrica masurata in C/m, p este coeficientul piroelectric in unitati de C/mK, iar θ este temperatura in K sau C.

Pentru a masura separat cele doua componente materialul este montat in asa fel incit sa nu se poata deforma si deci componenta indirecta (piezoelectrica) sa nu fie activata. Cele doua efecte pot actiona in acelasi sens sau in sensuri contrare, determinind astfel coeficientul piroelectric total. In general efectul primar este mai puternic, dar exista si exceptii, printre care chiar turmalina. Exista si un efect tertiar, care apare atunci cind materialul este supus unei incalziri sau raciri neuniforme, ceea ce produce o tensiune mecanica neuniforma si o polarizare electrica printr-un efect piezoelectric.

In productia de detectori de infrarosu si unde milimetrice este importanta alegerea unui material cu un coeficient piroelectric cit mai mare, de exemplu C₆H₁₇N₃O₁₀S (triglycine sulfate) cu un coeficient piroelectric total de −270 μC/mK. Pentru comparatie turmalina are un coeficient cu aproape doua ordine de marime mai mic, −4 μC/mK.

II. Istoric

Piroelectricitatea este cunoscuta inca din antichitate, cind hindusii si grecii au constatat ca de exemplu cristalele de turmalina capata prin incalzire proprietatea de a atrage obiectele usoare (cenusa etc.). In secolul al IV-lea i.Hr. (aproximativ anul 315 i.Hr.) invatatul grec Teofrast a descris o piatra pe care el o numea lyngourion (in latina lyncurium) si care atrage paiele si aschiile de lemn. Aceasta piatra este cel mai probabil ceea ce azi numim turmalina. Teofrast credea ca acest material se formase din urina unui animal salbatic, pe care mai tirziu Plinius l-a identificat cu risul (Lynx lynx).

Secolul al XVII-lea

Timp de peste doua milenii cunostintele noastre despre piroelectricitate nu au evoluat aproape deloc, pina cind in secolul al XIII-lea aceasta a intrat in atentia citorva invatati. In medicul si chimistul Louis Lemery a realizat prima descriere stiintifica a fenomenului. Primul care a inteles ca proprietatile turmalinei au de a face cu electricitatea a fost insa naturalistul Carl von Linn, care pe baza acestei observatii a numit turmalina lapis electricus (piatra electrica). O serie de alti cercetatori ai secolului al XVIII-lea au continuat sa studieze fenomenul, dar intelegerea cantitativa a acestuia avea sa se produca abia in secolul urmator, in urma dezvoltarii unor aparate suficient de precise.

Secolul al XIX-lea

La inceputul secolului al XIX-lea David Brewster, fizician cu importante contributii in optica, a studiat si proprietatile piroelectrice ale sarii Rochelle (tartrat de sodiu si potasiu). Dupa inventarea electrometrului de catre Antoine Becquerel au devenit posibile determinari cantitative ale piroelectricitatii; primul care a efectuat astfel de masuratori a fost John Mothe Gaugain. El a descoperit citeva din caracteristicile importante ale piroelectricitatii:

• Sarcina electrica produsa de un cristal de turmalina depinde numai de limitele intre care variaza temperatura sa.
• Intre doua limite de temperatura date, cresterea temperaturii produce aceeasi electricitate ca scaderea acesteia, dar sarcina electrica are semnul opus.
• Cantitatea de sarcina electrica este direct proportionala cu aria sectiunii transversale a cristalului, dar nu depinde de lungimea acestuia.

In William Thomson a elaborat o teorie despre piroelectricitate si a prezis cu aceasta ocazie existenta fenomenului invers, electrocaloric.

Fratii Pierre si Jacques Curie au descoperit o parte din mecanismele responsabile pentru efectul piroelectric, ceea ce i-a condus in cele din urma la descoperirea piezoelectricitatii in .

Secolul al XX-lea

In deceniile ce au urmat piroelectricitatea a fost studiata de numerosi oameni de stiinta printre care si citiva laureati ai Premiului Nobel, cunoscuti in general pentru realizari in alte domenii, precum Wilhelm Rntgen, Pierre Curie, Gabriel Lippman, Heike Kammerlingh Onnes, Erwin Schrdinger, Archer Martin si Max Born.

Studiile lui Joseph Valasek asupra piroelectricitatii aveau sa duca in la descoperirea unui alt fenomen inrudit, feroelectricitatea.

In chimistul Yeou Ta de la Sorbona a propus ca aplicatie a piroelectricitatii turmalinei utilizarea acesteia la detectia radiatiilor infrarosii. In timpul si dupa terminarea celui de-al doilea razboi mondial cercetarile au continuat in SUA, Regatul Unit si Germania, dar rezultatele au fost tinute secrete. Abia incepind din anii 1960 au inceput sa fie publicate descrieri ale unor detectori piroelectrici.

In prezent, structura unui asemenea detector cuprinde materialul piroelectric si electronica necesara pentru amplificarea semnalului. Cele mai utilizate materiale piroelectrice sint TGS (triglycine sulfate), tantalatul de litiu, unele ceramici pe baza de zirconat si titanat de plumb, unii polimeri fluorurati etc.

III. Principiul de functionare

Principiul de functionare consta in absorbtia radiatiei incidente in materialul piroelectric, ceea ce conduce la o mica variatie a temperaturii. Ca urmare a efectului piroelectric, pe suprafetele materialului sensibil se acumuleaza sarcini electrice, colectate de electrozii depusi pe aceste suprafete si transportate la amplificatorul de inalta impedanta de intrare. De obicei acesta este un tranzistor cu efect de cimp (FET) sau contine la intrare un asemenea tranzistor.

Detectorii piroelectrici sint sensibili numai la variatia fluxului de radiatie incident. De aceea in fata detectorului se plaseaza adesea un chopper optic, un dispozitiv care intrerupe periodic fluxul de radiatie. In lipsa acestuia detectorul poate surprinde numai miscarea tintei sau variatia temperaturii sale.

In aplicatii se foloseste fie un singur detector, fie un sir liniar sau chiar o matrice bidimensionala de asemenea sensori. Varianta din urma, impreuna cu optica adecvata, se foloseste pentru a genera imagini termice in care obiectele mai calde se vad mai stralucitoare, cu diverse aplicatii posibile.

IV. Avantaje

In comparatie cu detectorii care se bazeaza pe efectul fotoelectric, detectorii piroelectrici au o serie de avantaje importante:

• sensibilitate intr-un interval spectral foarte larg, teoretic intregul spectru electromagnetic, depinzind numai de absorbtia radiatiilor in cristal si in electrozi;
• posibilitatea de a utiliza detectorul intr-o gama larga de temperaturi, de la citeva grade kelvin pina la citeva sute de grade, deci inclusiv la temperatura camerei;
• consum foarte redus de putere electrica;
• timp de raspuns foarte redus, in unele cazuri de numai citeva picosecunde;
• cost de productie foarte redus.

Dezavantajul esential al detectorilor piroelectrici este sensibilitatea redusa.

V. Detector piroelectric sub actiunea radiatiei termice

Pentru analiza fenomenului piroelectric consideram geometria din fig.1. Radiatia incidenta pe materialul piroelectric o consideram de forma:

(1)

Ecuatia de continuitate pentru fluxul termic se scrie in forma:

(2)

(adica ceea ce se absoarbe din radiatia incidenta minus ceea ce se pierde prin radiatie determina incalzirea materialului pirodetector ).

in care: C -capacitatea calorica a detectorului de radiatie,

G -conductanta termica de la detector spre mediul inconjurator,

T_o -temperatura mediului ambiant,

-coeficientul de absorbtie.

Solutia ecuatiei (2) este de forma:

(3)

in care marimea este complexa si independenta de timp.

Introducand expresia lui T in ec.(2) se obtine cu :

care da, pentru complex, urmatoarea ecuatie :

din care se obtine:

(4)

In ec.(4) este constanta de timp termica a detectorului iar .

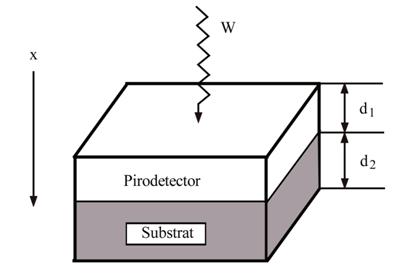
Figura 1. Schema unui pirodetector.

Daca rationalizam pe in ec.(4), rezulta:

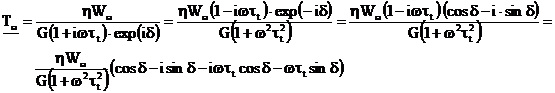
Modulul lui se obtine simplu din ultima ecuatie:

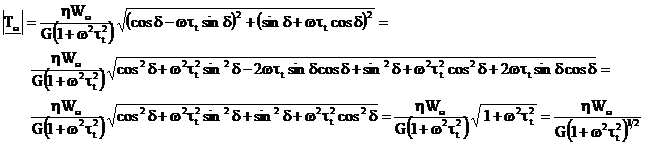
sau:    (5)

Cu acestea ecuatia (3) pentru unda de temperatura in materialul pirodetectorului se obtine in forma:

(6)

In situatia in care , forma ecuatiei (5) se simplifica:

(7)

De asemenea in situatia in care , forma ecuatiei (5) se simplifica:

(8)

Pentru a explicita si dependenta lui de coordonata x avem in vedere relatiile care exprima proportionalitatea dintre fluxul termic Q si gradientul de temperatura, [2]:

(9)

Divergenta lui Q fiind egala cu cantitatea de caldura care iese din unitatea de volum a corpului in unitatea de timp, putem scrie:

(10)

Din cele doua relatii (9) si (10), rezulta:

sau echivalent: (11)

In cazul unidimensional, ec.(11) se scrie:

(12)

in care:    D -coeficientul de difuzibilitate termica,

-densitatea materialului,

c -caldura specifica,

k -coeficientul de conductibilitate termica.

In cazul problemei considerate, a pirodetectorului, in care temperatura depinde de timp si coordonata, , ecuatia (12) se scrie:

(13)

Prin urmare solutia generala pentru unda de temperatura care strabate pirodetectorul este:

(14)

in care este adancimea de patrundere a undei de temperatura.

Daca se introduce ec.(14) in ec.(13) se poate deduce relatia dintre si D. Avem succesiv:

si deci:

din care rezulta imediat:

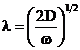sau (15)

Se poate observa ca la frecvente suficient de mici se poate intampla ca iar de la o anumita frecventa .

Frecventa la care unda de temperatura "umple" intreg detectorul, ceea ce este echivalent afirmatiei ca , se obtine din considerentele care urmeaza. La putem scrie ca: si deci: 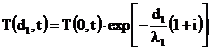iar:

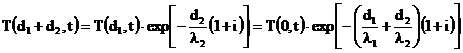(16)

Prin urmare lungimea de patrundere a undei de temperatura este egala cu daca exponentul din ec.(16) este egal cu unu adica:

(deci intensitatea undei de temperatura scade de e ori).

Prin urmare:    . Cum, din ec.(15), 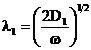, rezulta imediat:

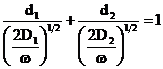
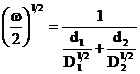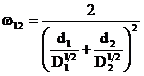si deci:    sau (17)

Pentru , capacitatea calorica C descreste odata cu cresterea frecventei astfel incat:

a) pentru ; (18)

In relatia (18) am pus in evidenta dependenta de frecventa a lui C prin relatia:

b) pentru : (19)

c) : (20)

Daca logaritmam relatiile (18),(19) si (20), se obtine echivalent:

a) pentru ; 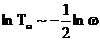(18')

b) pentru : (19')

c) : (20')

Reprezentarea grafica a relatiilor (18'), (19') si (20') este data in fig.2.

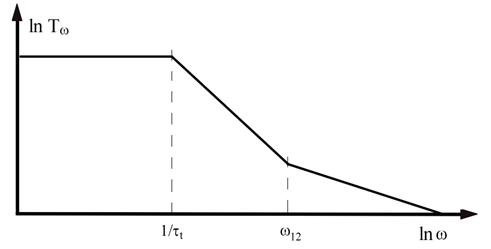
Figura 2. Dependenta temperaturii de frecventa in scara dublu logaritmica,.

VI. Tensiunea la bornele detectorului

Pentru a calcula tensiunea care apare la bornele detectorului, utilizam relatia:

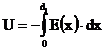(21)

relatie care rezulta din definitia intensitatii campului electric: .

Intrucat , din care , polarizarea totala va fi:

(22)

al doilea termen din dreapta egalitatii (respectiv P₁) fiind datorat polarizarii induse de campul electric.

Deoarece in conditii de circuit deschis, rezulta ca: sau: .

Din ultima egalitate rezulta: (23)

in care este coeficientul piroelectric.

Revenind la relatia care da tensiunea la bornele pirodetectorului si avand in vedere ec.(23), se poate scrie:

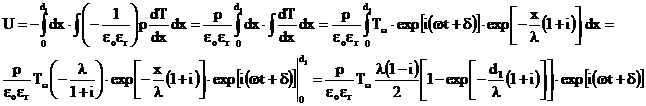
adica:

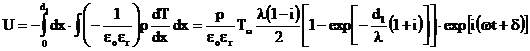(24)

Figura 3. Succesiunea , , pe axa frecventelor.

Avand in vedere dispunerea relativa pe axa frecventelor, in care este frecventa la care unda de temperatura "umple" numai materialul detectorului, conform fig.3 rezulta:

a)

In aceasta situatie iar 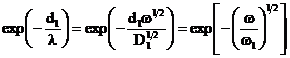, deci: , deoarece am presupus . In aceste conditii tensiunea la bornele pirodetectorului este de forma:

adica in situatia , ,sau (25)

b) , situatie in care . In aceste conditii tensiunea la bornele pirodetectorului este de forma:

, adica sau (26)

Am folosit pentru tensiunea U o expresie similara celei utilizate la punctul a) in care dar cu alta valoare pentru , data de considerentele descrise mai sus.

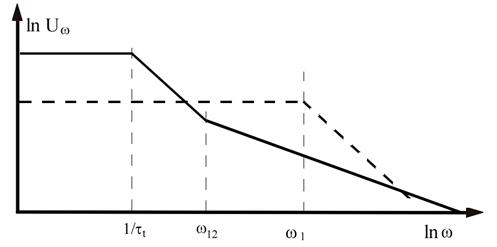
Figura 4. Dependenta grafica a tensiunii la bornele unui pirodetector in scara dublu logaritmica . Daca este independent de frecventa,

are forma reprezentata prin linie intrerupta.

c) 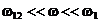situatie in care . In aceste conditii tensiunea la bornele pirodetectorului este de forma:

, adica sau (27)

d) situatie in care . In aceste conditii tensiunea la bornele pirodetectorului este de forma:

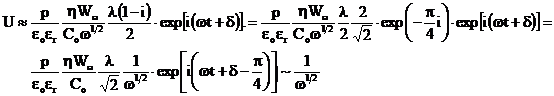
adica sau (28)

si in care am folosit .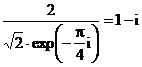

Reprezentarea grafica a dependentei in situatiile expuse la punctele este data in figura 4.

VII. Curentul piroelectric

Curentul piroelectric se obtine din relatia , Z fiind impedanta pirodetectorului si este data de expresia:

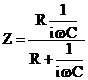(29)

in care: R -este rezistenta legata in paralel pe detector (in schema echivalenta),

C -capacitatea detectorului si a circuitului de masura.

Relatia (29) se mai poate pune in forma:

(30)

in care: -constanta de timp electrica a grupului RC.

Daca rationalizam ec.(30), se obtine:

si deci modulul impedantei se scrie:

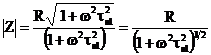(31)

In aceste conditii curentul piroelectric capata forma:

(32)

iar pentru relatia se scrie simplu: .

Deoarece ordinea frecventelor de interes este: , dependenta curentului piroelectric de frecventa este:

A)

Tensiunea U este de forma (punctul a) de mai sus):

si deci:

(33)

in care am tinut cont, in expresia impedantei pirodetectorului, ca frecventa (frecventa fiind foarte joasa).

Din aceste considerente se observa ca:

sau echivalent (34)

B)

In aceasta situatie:

(35)

in care am tinut cont ca in situatia data si in consecinta .

Din aceste considerente se observa ca:

sau echivalent (36)

C)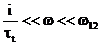

In aceasta situatie:

(37)

in care am tinut cont ca si de aceasta data ca si in consecinta .

Din aceste considerente se observa ca:

sau echivalent 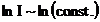(38)

D)

In aceasta situatie:

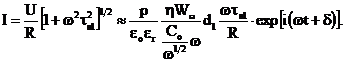(39)

in care am tinut cont din nou ca si in consecinta .

Din aceste considerente se observa ca:

sau echivalent (40)

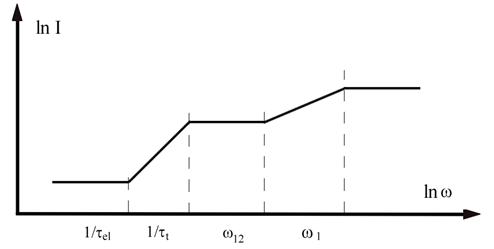
Figura 5. Dependenta grafica a responsivitatii in curent a unui pirodetector

in scara dublu logaritmica,    .

E)

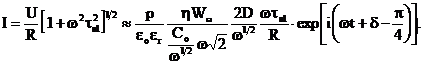(41)

Din aceste considerente se observa ca:

sau echivalent 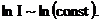(42)

Reprezentarea grafica a dependentei in situatiile expuse la punctele este data in fig.5.

VIII. Responsivitatea in curent si in tensiune a unui pirodetector

Revenim la relatia pentru tensiunea care apare la bornele detectorului in cazul in care si care este de forma:

(43)

In aceasta situatie relatiile pentru si capacitatea calorica C a detectorului de radiatie sunt de forma:

, respectiv (44)

unde:    c -caldura specifica a materialului detectorului,

A -aria detectorului,

-adancimea de patrundere a undei de temperatura,

-densitatea materialului pirodetectorului.

Cu acestea ec.(43) se scrie:

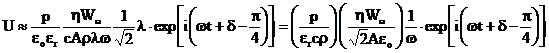
Primul factor este determinat de proprietatile materialului detectorului piroelectric si reprezinta "factorul de merit". El se constituie ca un criteriu important in alegerea unui material pentru construirea detectorilor de radiatie.

Consideram ca sarcina de pe armaturile detectorului este proportionala cu diferenta de temperatura , aria detectorului A si coeficientul piroelectric p al materialului piroelectric, adica:

(46)

In aceasta situatie, curentul instantaneu care trece prin detector, cand acesta este expus radiatiei infrarosii este:

(47)

Definim responsivitate in curent ca:

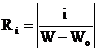si deci 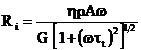(48)

Tensiunea instantanee la bornele pirodetectorului este:

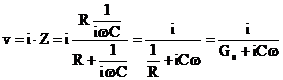
sau:    (49)

Definim responsivitate in tensiune ca:

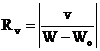si deci 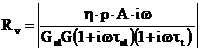(50)

si din care rezulta prin calcule asemanatoare ca pentru (cu rationalizarile de rigoare)

(51)

Avand in vedre ec.(51), se obtin urmatoarele aproximatii utile pentru responsivitatea in tensiune:

1) pentru frecvente adica (52)

si deci .

2) pentru frecvente adica (53)

si deci .

3) ) pentru frecvente adica (54)

si deci .

Reprezentarea grafica a dependentei in situatiile expuse la punctele este data in fig.6.

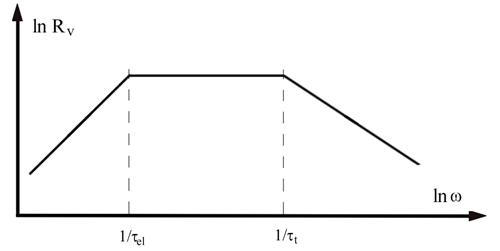
Figura 6. Dependenta grafica a responsivitatii in tensiune a unui pirodetector

in scara dublu logaritmica, .

Se defineste detectivitatea unui dispozitiv de pirodetectie ca:

(55)

in care este tensiunea echivalenta de zgomot a detectorului.

IX. Montajul    experimental

proba

frecventa

osciloscop

Generator de tensiune

Figura 1. Montajul experimental

X. Date experimentale

Scopul lucrarii era de a determina responsivitatea in tensiune in functie de ω, dar asa cum s-a aratat mai devreme, R_V este proportional cu U (tensiunea), iar ω este proportional cu ν, astfel incat practic, in laborator am masurat tensiunea in functie de frecventa (de fapt, amplitudinea semnalului vizionat cu ajutorul osciloscopului ). Datele experimentale au fost apoi tabelate si reprezentate grafic.

Se cunoaste valoarea C=40 pF, iar formula de calcul a R este : .

Rezulta ca

Tabelul 1. Datele experimentale

Reprezentam grafic dependenta frecventei in functie de tensiune :

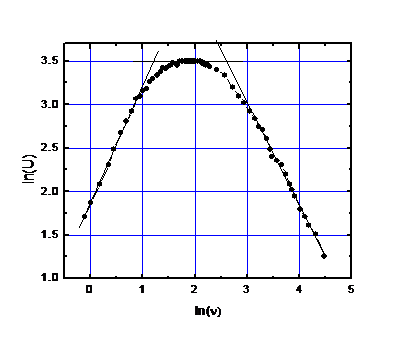
Figura 8. Dependenta grafica a tensiunii unui pirodetector

in scara dublu logaritmica, .

Avand in vedere dependenta cunoscuta a responsivitatii in functie de ω , am trasat linii care fiteaza datele noastre experimentale astfel incat forma graficului sa se apropie cat mai mult de forma dependentei ln(R_V)=f(ln(ω)) .

Din acest grafic gasim si si deci valorile , respectiv .

Determinam R cu ajutorul formulei , si cunoscand valoarea C=40 pF :

Iar pentru valoarea lui    gasim .