Simularea numerica a campului magnetic cvasistationar

Simularea numerica a problemelor de camp macroscopic se bazeaza -in principal- pe formularea variationala echivalenta modelelor diferentiale care descriu local starea campului, dar si pe discretizarea acestor modele diferentiale. Modelele discrete fiind prezentate pe larg in lucrarea noastra Dumitrescu, I. (1983), in acest paragraf se va aborda numai modelarea variationala.

Modelul variational de camp magnetic cvasistationar

Acest model se deduce prin particularizarea adecvata a integralei de actiune (V1), prezentata in paragraful 2.6.3, si asocierea conditiilor de unicitate a determinarii campului magnetic cvasistationar (definite in paragraful 5.2.1). Intre aceste conditii de unicitate, o importanta aparte revine conditiei de etalonare a lui Coulomb (v. 5.1.1), necesara pentru definire univoca a potentilului magnetic vector.

Se poate demonstra ca pentru functionala energetica asociata campului magnetic cvasistetionar in medii oarecare este suficient sa se considere expresia:

,

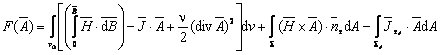in care, este volumul domeniului de camp (reprezentand o regiune a spatiului tridimensional), marginit de suprafata , este versorul normalei la (cu sensul spre interiorul ei), reprezinta o eventuala suprafata de discontinuitate din avand o panza de curent electric de conductie cu densitatea , iar si reprezinta vectorii de stare magnetica a campului (intensitatea lui, inductia magnetica si potentilal magnetic vector) si electrocinetica a mediului din (prin densitatea curentului electric de conductie).

Primii doi termeni ai integralei de volum (5.171) se obtin direct din functionala generala (2.68), corespunzator conditiilor regimului magnetic cvasistationar (care impun: si ).

Integrala pe din expresia (5.171) include conditiile pe frontiera de tip Newmann (v. 2.2.3); ea se anuleaza pentru componenta tangentiala la nula a potentialului magnetic vector (adica pentru ) sau pentru componenta tangentiala la nula a intensitatii campului magnetic ( adica pentru ) deoarece intotdeauna produsul vectorial este normal pe versorul (deci este tangent la , ceea ce implica: ).

Ultimul termen integral din membrul drept al relatiei (5.171) exprima conditia de interfata ce se refera la o eventuala suprafata fixa de discontinuitate pe care exista . Ecuatiile de trecere si (in care intervin rotorul si divergenta de suprafata relativa la ), caracteristice campului magnetic cvasistationar, reprezinta conditiile la limita naturale in procesul de stationarizare a functionalei (5.171).

In fine, termenul din functionala (5.171) impune conditia lui Coulomb , de etalonare pentru potentialul magnetic vector (v. 5.1.1) in functionala energetica (5.171), conform metodei asa-zisei functii de penalitate (notiune introdusa de Coulomb, J.L. , in anul 1981, prin teza sa de doctorat sustinuta la Institutul National Politehnic din Grenoble - Franta, cu titlul "Analyse tridimensionelledes champ lectriques et magntiques par la mthod des lments finis "). Pe scurt, aceasta metoda consta in : daca , definita pe , reprezinta o functionala de stationarizat conform unui principiu variational conventional si daca se impune -suplimentar- satisfacerea unei restrictii de egalitate pe , atunci se poate adopta ca functionala modificata, -corespunzatoare principiului variational constrans- expresia , unde (numit parametru de penalitate) este un numar real, pozitiv, suficient de mare pentru ca restrictia impusa sa fie "cat mai bine" indeplinita. In cazul de aici, si . Parametrul de penalitate din acest caz, , cu dimensiunea unei reluctivitati (adica ), este dependent de materialul si starea fizica a mediului din campul .

Prin explicitarea ecuatiei constitutive cu forma generala sau -adica legea legaturii dintre , si (magnetizatia)- se obtin formele specifice ale functionalei energetice (5.171), asociata campului magnetic cvasistationar, asa cum se va arata in urmatoarele doua aplicatii.

Aplicatia 5.1 Se considera cazul: medii fixe, neliniare, anizotrope, neomogene si magnetizate permanent, pentru care se cere sa se stabileasca ce forma va avea functionala (5.171).

In cazul unor astfel de medii, adica: imobile (ceea ce inseamna ca viteza este , fiind raza vectoare a unui punct fata de un punct de referinta ); neuniforme (neomogene si cu ortotropie magnetica) si neliniare - ceea ce implica faptul ca marimile de material si depind de vectorul inductiei magnetice si de , astfel ca (de exemplu) reluctivitatea se exprima printr-un tensor , avand si inductie magnetica remanenta , din cauza magnetizatiei permanente, legea legaturii dintre , si -adica ecuatia constitutiva - se scrie sub forma:

. (5.1-1)

Atunci, cu aceasta ecuatie constitutiva (5.1-1), functionala energetica de stationarizat (5.171) ia forma:

,(5.1-2)

in care reprezinta norma canonica a matricei patrate asociate tensorului simetric de ordinul doi, , al reluctivitatii materialului din .

Functionala (5.1-2) se obtine direct, prin inlocuirea lui din primul termen al functionalei generale (5.171) cu expresia sa din ecuatia constitutiva (5.1-1).

Aplicatia 5.2. Se considera cazul: medii fixe, liniare, izotrope, omogene si nemagnetizate permanent, pentru care se cere sa se stabileasca ce forma va avea functionala (5.171).

In cazul acestor medii (liniare, uniforme, imobile -adica avand peste tot in - si cu in orice punct din ) de camp magnetic cvasistationar, reluctivitatea devine o constanta scalara iar inductia remanenta este nula, .

Ca urmare, in aceasta situatie, functionala energetica de stationarizat se poate obtine prin simpla particularizare (la acest caz, al aplicatiei 5.2) a expresiei (5.171) sau prin scrierea ei in forma specifica determinata de faptul ca (mediul neavand nici histerezis), ceea ce conduce la forma:

,

in care suma se refera la componentele scalare ale potentialului magnetic vector .

In prima integrala din expresia (5.2-1), functia de penalitate pentru impunerea conditiei de etalonare a lui Coulomb (adica ) nu mai apare, deoarece aceasta conditie (restrictie) este satisfacuta implicit.

A doua integrala a functionalei (5.2-1) corespunde unor conditii mixte la limita, pe . Aceasta integrala se anuleaza pentru conditia Neumann omogena pe , unde este portiunea din frontiera pentru care se da conditia la limita de tip Neumann (referitoare la variatia lui pe directia normalei la ). Conditia de tip Dirichlet, adica , reprezinta singura conditie la limita esentiala, relativ la (5.2-1). Ca urmare, ea trebuie impusa explicit clasei de functii in care se cauta solutia de potential magnetic vector ce realizeaza valoarea stationara a functionalei (5.2-1). Desigur, s-a inteles ca in cele precedente, indicile N se refera la conditiile de tip Neumann si D la cele Dirichlet, care pot fi formulate pe portiunile de frontiera si , astfel ca .

Analiza numerica a problemelor tridimensionale de camp magnetic cvasistationar

Se considera cazul cel mai des intalnit in aplicatiile tehnice (al circuitelor feromagnetice - v. cap6), in care materialul din domeniul este uniform insa neliniar. Domeniul este deschis si limitat in , iar potentialul magnetic vector are trei componente: , care intr-un sistem cartezian ( se scrie , unde este versorul directiei .

In acest caz, functionala energetica (5.2.-1) devine:

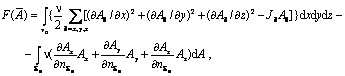
deoarece, prin definitie , cu versorul directiei normalei la data de , astfel ca .

Pentru rezolvarea unei probleme practice pe cale numerica ( de exemplu, prin aproximatia solutiei prin tehnica elementelor finite - v. 9.2.4) este suficient ca functionalei (5.172) sa i se ataseze conditii pe frontiera de tip Neumann: , , -ca o conditie la limita naturala in procesul de stationarizare al functionalei (5.2-1)- functia fiind exprimata numeric conform problemei practice formulate si modului de partitie a elementelor finite pe , care conduce la o retea spatiala de discretizare.

Atunci studiul unei probleme tridimensionale consta in:

i) fie o deschidere limitata in , cu frontiera suficient de regulata, pentru care se noteaza:

pe } ,

in care: este un spatiu Hilbert, desemneaza spatiul Sobolev si este o variabila vectoriala astfel ca pe frontiera componenta tangentiala este nula;

ii) se considera acea variabila a spatiului care da produsul scalar:

.

In fapt aplicatia:

este o norma pe , echivalenta normei introduse prin norma obisnuita a lui , adica:

;

iii) in aceste conditii -i) si ii)- oricare ar fi si , exista expresia:

, (5.174)

ceea ce se poate demonstra usor pentru functiile suficient de regulate si prin trecerea la limita pentru ;

iu) tinandu-se seama de aceste rezultate, problema tridimensionala se reduce la problemele variationale urmatoare:

a) sa se gaseasca astfel ca

(5.175)

si

b) sa se gaseasca astfel ca

, (5.176)

probleme care admit fiecare o solutie si numai una. In functionalele energetice (5.175) si 5.(176) -ca parametru de penalitate- este reluctivitatea materialului din ;

u) solutia , adica potentialul magnetic vector, a problemei (5.176) corespunzatoare cazului general (si, de asemenea, a problemei (5.175) pentru cazul materialelor liniare) este solutia problemei campului magnetic stationar care verifica conditia .

Solutia problemei b) se obtine rezolvandu-se ecuatia (5.176) in sensul distributiilor (D:

in ,

si pentru ca , rezulta imediat ecuatia lui Maxwell .

Pentru aproximarea numerica a solutiei problemelor (5.175) sau (5.176), domeniul de existenta din a campului magnetic stationar se partajeaza in tetraedre adecvate geometriei sistemului, pe care potentialul magnetic vector se aproximeaza prin functia discreta (pe tetraedre) , in spatiul functional (care il aproximeaza pe ):

pe pe

unde reprezinta tetraedrul. Atunci un element are urmatoarea forma explicita (intr-un sistem cartezian ):

,

in care, reprezinta volumul tetraedrului apartinand sistemului de tetraedrizatie ; este functia caracteristica a tetraedrului ; si sunt functii ale coordonatelor varfurilor tetraedrului, iar este valoarea functiei in varful al tetraedrului .

Atunci problema aproximativa, in tridimensional, pentru campul magnetic cvasistationar consta in gasirea lui astfel ca

,

unde este functionala energetica relativa la (5.176).

Aceasta problema (5.177) -discreta- de optimizare in admite un rezultat unic, solutiile fiind caracterizate -daca variabilele problemei sunt numerotate de la 1 la - prin:

(5.178) ,

rezolvarea numerica facandu-se printr-o metoda iterativa.

Aplicatia 5.3. Sa se determine, prin simularea numerica in 3D de tipul (5.176) si (5.178), campul inductiei magnetice in intrefierul tridimensional al unui alternator (v. Masini electrice).

Se considera ca reluctivitatea relativa a materialului feromagnetic al circuitului magnetic al alternatorului, adica (stiind ca , cu pentru aer/vid) are forma:

din figura 5.29.

Pentru a putea fi utilizata in sistemul de calcul automat, ea se introduce intr-un fisier din memoria 'hard-disc' a calculatorului prin scanare (cu un 'scaner'). Daca nu se dispune de o caracteristica (ca cea din figura 5.29) de precizie, atunci se poate exprima ( cu o aproximatie suficient de buna) prin expresia analitica:

dedusa din distributia punctelor in planul rezultata din curba de magnetizare a materialului (v. cap.6), cu urmatoarele valori ale parametrilor: ; ; si care are o eroare de aproximare a curbei din figura 5.29 de 3 la 4%.

Domeniul tridimensional ales (redat frontal in figura 5.30) a fost decupat (partajat) in 6160 tetraedre si 1140 noduri.

Prin utilizarea unui produs informatic ANSIS EMAG (v. 9.3.2) s-au obtinut -pe o statie de calcul IBM RISC System/600- rezultatele scontate, dintre care in figura 5.31 este redat spectrul liniilor de camp magnetic (ale inductiei magnetice ), din zona rotor -intrefier/crestaturi- stator, obtinute cu o imprimanta cu jet de cerneala.

De fapt, in figura 5.30 este prezentata, numai ca principiu constructiv, o sectiune transversala (normala pe axa masinii) prin circuitul magnetic al alternatorului cu o singura pereche de poli (fig. 5.30a) insotita de un fragment cu detalierea formei crestaturilor din miezul statoric (fig. 5.30b), pentru a intelege de ce -in vederea simularii numerice in 3D a campului magnetic prin metoda elementului finit- a fost necesara o 'stilizare' a circuitului magnetic tridimensional care sa permita partajarea lui in tetraedre (tetraedrizarea), conform schitei din figura 5.30c (care se refera numai la trei crestaturi).

In principiu, calculul numeric al campului magnetic stationar in 3D se face conform urmatorului algoritm (pe care produsul ANSIS EMAG il efectueaza automat):

- partitionarea in tetraedre a domeniului de studiat;

- se considera o functie vectoriala ce defineste potentialul magnetic vector pe . Aceasta functie este aleasa pe fiecare tetraedru, fiind continua in asa fel incat vectorul inductiei magnetice , care este dat de , sa fie constanta pe fiecare element tetraedric;

- se alege un punct din care 'porneste' in o linie de camp a lui . Acest punct apartine unui anumit tetraedru, in care se cunoaste directia liniei de inductie (), care este o constanta. Este suficient atunci, sa se traseze in acest element (tetraedru) o liniuta -care va reprezenta linia de inductie - al carui varf la dreapta va determina un punct situat in tetraedrul vecin;

- pentru vizualizarea liniilor de inductie magnetica in spatiu, se traseaza toate liniutele pe structura de tetraedre in care a fost partajat sistemul (asa ca in exemplul din figura 5.31).